Аксиомы линейного векторного пространства

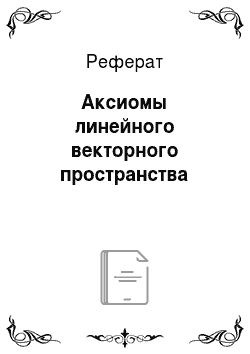
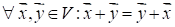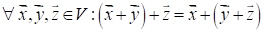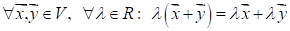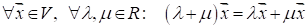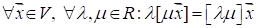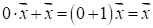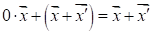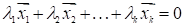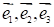Первая группа аксиом описывает отображение, называемое операцией сложения векторов, позволяет любым двум векторам и отнести третий вектор — их сумму так, что выполняются аксиомы:

V₁: Сложение векторов коммутативно.

V₂: Сложение векторов ассоциативно.

V₃: Существует нулевой вектор такой, что для справедливо равенство.

V₄: Для существует противоположный вектор такой, что .

Вторая группа аксиом описывает отображение, называемое операцией умножения вектора на число, при этом каждому вектору и числу однозначно отнести вектор, называемый произведением вектора на число, так что выполняются аксиомы:

Аксиомы линейного векторного пространства.

V₅: Операция умножения дистрибутивна по отношению к сложению векторов.

V₆: Операция умножения дистрибутивна по отношению к сложению чисел.

V₇: Операция умножения вектора на число ассоциативна.

V₈: Операция умножения вектора на единицу не меняет вектора .

Теорема 1.5. Произведение любого вектора на число 0 равняется нулевому вектору.

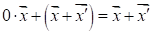
Доказательство. С одной стороны, имеем. С другой стороны, прибавляя почленно к обеим частям полученного равенства вектор, противоположный к вектору, мы получим. Таким образом,, т. е.

Теорема 1.6. Противоположный вектор для вектора равен, т. е. .

Теорема 1.7. Произведение вещественного числа на нулевой вектор равняется нулевому вектору, т. е. .

Система векторов называется линейно зависимой, если равенство выполняется для некоторых постоянных, причем.