Теоремы о дисперсии случайной величины

Теорема 6. Неслучайную величину можно выносить за знак дисперсии, возводя ее в квадрат.

Если с — неслучайная величина, а X — случайная, то.

Доказательство. По определению дисперсии.

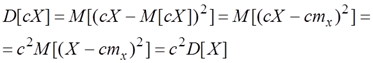
Следствие.

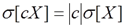
т. е. неслучайную величину можно выносить за знак среднеквадратического отклонения ее абсолютным значением. Доказательство получим, извлекая корень квадратный из формулы (7.2.1) и учитывая, что среднеквадратическое положительная величина.

Теорема 7. Дисперсия неслучайной величины равна нулю

Если с — неслучайная величина, то, тогда.

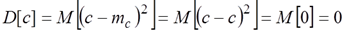
Теорема 8. Дисперсия суммы двух случайных величин равна сумме их дисперсий плюс удвоенный корреляционный момент:

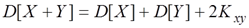
Доказательство. Обозначим По теореме сложения математических ожиданий Перейдем от случайных величин X, Y, Z к соответствующим центрированным величинам X, Y, Z. Вычитая почленно из равенства (7.2.5) равенство (7.2.6), имеем:

По определению дисперсии.

что и требовалось доказать.

Формула для дисперсии суммы может быть обобщена на любое число слагаемых:

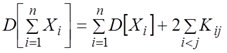
где Кij — корреляционный момент величин X_i , X_j, знак i<j под суммой обозначает, что суммирование распространяется на все возможные попарные сочетания случайных величин (X₁ , Х₂…,Х_n).

Доказательство аналогично предыдущему и вытекает из формулы для квадрата многочлена.

Формула может быть записана еще в другом виде:

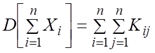
где двойная сумма распространяется на все элементы корреляционной матрицы системы величин (Х₁, Х₂,…Х_n), содержащей как корреляционные моменты, так и дисперсии.

Если все случайные величины (Х₁, Х₂,…,Х_п), входящие в систему, некоррелированы (т. е. Кij = 0 при ij). формула (7.2.7) принимает вид:

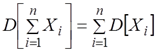
т.е. дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых.

Это положение известно под названием теоремы сложения дисперсий.

Теорема 9. Дисперсия линейной комбинации случайных величин определяется соотношением

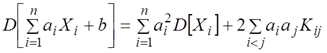
где К_ij— корреляционный момент величин X_i, X_j.

Доказательство. Введем обозначение:

Тогда.

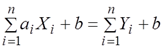
Применяя к правой части выражения (7.2.11) формулу (7.2.7) для дисперсии суммы и учитывая, что D[b] = 0, получим:

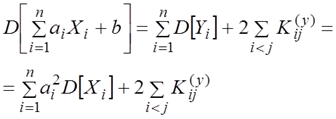
где — корреляционный момент величин Y_i, Y_j.

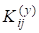
Вычислим этот момент. Имеем:

Отсюда.

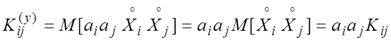
В частном случае, когда все величины (Х₁, Х₂,…,Х_n) некоррелированные, формула принимает вид:

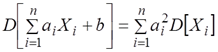
т.е. дисперсия линейной функции некоррелированных случайных величин равна сумме произведений квадратов коэффициентов на дисперсии соответствующих аргументов).

Теорема 10. Дисперсия произведения независимых случайных величин определяется соотношением

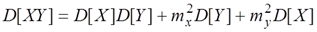
Доказательство. Обозначим XY=Z. По определению дисперсии.

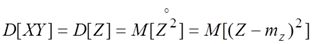
Так как величины X, Y независимы, m_z = m_xm_y и.

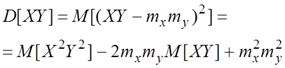
При независимых X, У величины Х², Y² тоже независимы следовательно,.

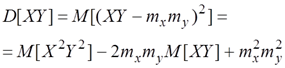
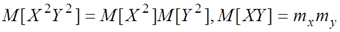
Но М[X²] есть не что иное, как второй начальный момент величины X, и, следовательно, выражается через дисперсию:

Аналогично.

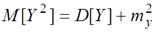
Подставляя выражения (7.2.16) и (7.2.17) в формулу (7.2.15) и приводя подобные члены, приходим к формуле (7.2.14).

В случае, когда перемножаются центрированные случайные величины (величины с математическими ожиданиями, равными нулю), формула (7.2.14) принимает вид:

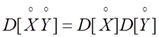
т.е. дисперсия произведения независимых центрированных случайных величин равна произведению их дисперсий.