Анализ динамики себестоимости зерна по двум хозяйствам

Рядом динамики называется ряд статистических показателей, характеризующих изменение общественных явлений во времени. Для всесторонней характеристики направления и интенсивности развития изучаемого явления путём сопоставления уровней исходного ряда следует рассчитать и проанализировать систему показателей: абсолютный прирост, коэффициент роста, темп прироста, значение 1% прироста.

Показатели рассчитываются по формулам:

Абсолютный прирост:

базисный:

цепной: ;

Коэффициент роста:

базисный:; цепной:

Темп прироста:

базисный:; цепной:

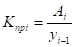
Значение 1% прироста:

П= Ап/Т.

Абсолютный прирост представляет собой разность между двумя исходными уровнями, один из которых принят за базу сравнения. При условии, что за базу сравнения принимается каждый предыдущий уровень — абсолютный прирост — цепной, если за базу сравнения берётся начальный уровень — базисный.

Коэффициент роста — это отношение двух исходных уровней, один из которых принят за базу сравнения (базисный или цепной).

Коэффициент роста, выраженный в процентах, называется темпом роста. Он показывает, сколько процентов изучаемый уровень составит от базы сравнения.

Темп прироста показывает, на сколько процентов изучаемый показатель больше или меньше базы сравнения, а также, сколько процентов составляет абсолютный прирост от базы сравнения.

Абсолютное значение 1% прироста показывает, сколько единиц в абсолютном значении приходится на 1% прироста или снижения.

Под влиянием случайных причин уровни динамических рядов часто сильно варьируют, а тенденция развития затушёвывается. Для её проявления в статистики используют специальные приёмы. Сглаживание ряда при помощи скользящей средней предполагает последовательный расчёт средних за периоды, сдвигаемые на одну дату.

Метод аналитического выравнивания заключается в отыскании такой линии, которая пройдёт в максимальной близости ко всем точкам (тренд).

Уравнение, отражающее тенденцию развития, имеет вид:

у = а₀ + а₁*t,.

где а₀ и а₁ — параметры уравнения,.

t — показатель времени.

Так как в рядах динамики значения являются показателями времени, то всегда можно придать им такое значение, чтобы их сумма была равна нулю. Для определения параметров уравнения составим систему из двух уравнений. Первое уравнение получаем путём умножения исходного уравнения на коэффициент при а₀ и суммированием произведений по всем наблюдениям:

?у = п* а₀ + а₁ ?t.

Второе уравнение получим путём умножения исходного уравнения на коэффициент при а₁ и суммированием по всем наблюдениям:

?уt = а₀?t + а₁?t².

Так как? t=0, то система упрощается:

• ?уt = а₀ п
• ?уt = а₁?t².

Выразим отсюда а₀ и а₁: а₀ =? у / п, а₁ = ?уt / ?t².

Очевидно, что а₀ — средний уровень динамического ряда, а₁ — среднее увеличение (уменьшение) изучаемого показателя.

Проведём динамический анализ себестоимости зерна по двух хозяйствам (табл. 4.6 и 4.7).

Таблица 4.6.

Расчёт показателей динамики себестоимости зерна в хозяйстве 1.

а₀ = 326,9/10= 32,69, а₁ = -166,2/110=-1,51.

Следовательно уравнение будет иметь вид: у = 32,69+(-1,51)*t.

Рис. 4.3 Динамический ряд себестоимости зерна в хозяйстве 1.

Динамический анализ представленный в таблице 4.1 показал, что за 10 лет в хозяйстве наблюдается снижение себестоимости зерна. По сравнению с 1995 в 2004 году данный показатель сократился с 38,6 до 26,44, то есть на 11,96 или на 31,1%.

Проводя анализ сравнения цепным способом в анализируемом периоде можно выделить две группы:

• — период роста (включая 1995 г.- 1996 г., где темп роста составил 104,69%, или в абсолютном выражении 1,6 ц.).
• — период снижения (1996;2004г., где темпы снижения составили 98,5, 97,2, 79,2, 95,4, 98,3, 97,9, 71,9,и 95,8%)

Данная ситуация возникла из-за экономической ситуации в стране, с переходом на рыночные отношения прекратилось финансирование сельского хозяйства, и им пришлось перейти на самофинансирование и самоокупаемость.

В таблице проведено выравнивание динамического ряда двумя способами мы видим, что анализируемый динамический ряд имеет тенденцию к снижению, что наглядно представлено на рисунке 4.3.

Проведём аналогичный динамический анализ по хозяйству с высокой продуктивностью. Данные этого анализа представлены в таблице 4.7 и рисунке 4.4.

Таблица 4.7.

Расчёт показателей динамики себестоимости зерна в хозяйстве 2.

а₀ =301,3 /1= 30,13, а₁ = -63,8/110= -0,58.

Следовательно, уравнение будет иметь вид: у = 30,13+(-0,58)t.

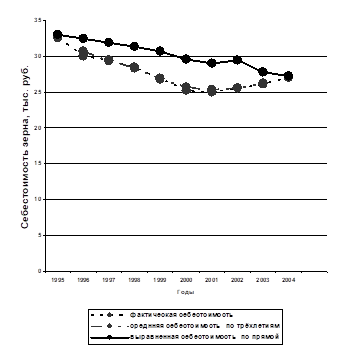
Рис. 4.4 Динамический ряд себестоимости в хозяйстве 2.

По данным, представленным в таблице 4.7 видно, что анализируемый показатель также как и в первом хозяйстве сокращается. Это так же произошло за счёт изменения факторов, которые оказывают влияние на анализируемый фактор. По таблице 4.7 видно, что начиная с 2002 года себестоимость начинает увеличиваться, хотя по выравненым данным видно, что в общем данный показатель имеет тенденцию с уменьшению. Проводя анализ сравнения между двумя хозяйствующими субъектами можно сделать следующий вывод, что себестоимость зерна за 10 лет снижается в первом хозяйстве, а во втором хозяйстве начиная, с 2002 года начинает увеличиваться, хотя и медленно.

Из выше сказанного следует, что изменение себестоимости зависит не только от факторов, которые приведены в разделе 2, но и от умения управлять хозяйством, а так же и от государственных программ развития сельского хозяйства.

Следующим этапом данной курсовой работы будет индексный анализ себестоимости зерна.