Введение. 
Эмпирические модели иерархииматериальных миров

Как теперь известно, на основании всех тех естественнонаучных моделей, изложенных в работах автора [1, 2] и др., с учётом эмпирических выводов и экспериментальных результатов физиков после А. Эйнштейна отмечены объективные основания СТЕРЕОХРОНОДИНАМИКИ — физической теории, способной создать математическую модель пространства-времени, которая должна обладать необходимой и достаточной гибкостью при описании всех свойств пространства-времени, включая обширные области современных физических явлений, то есть в соответствии с нашим выводом о полноте аксиоматики физических теорий для нашего 4-х мерного мира мы положили в основу ПЯТЬ фундаментальных аксиом, главной из которых является наша принципиально новая ПАРАДИГМА об атрибутивно — субстанциональной ПРИРОДЕ нашего мира.

С целью наполнения этой СТЕРЕОХРОНОДИНАМИЧЕСКОЙ АКСИОМАТИКИ конкретным физическим содержанием нам теперь необходимо каждую из ПЯТИ упомянутых аксиом подвергнуть эмпирической или экспериментальной проверке. Соблюдая порядок нумерации упомянутых аксиом [2], вспомним ПЕРВУЮ из них:

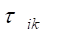
I. Все материальные объекты нашего мира в виде полей или вещественных тел представляют собой общую непрерывную среду — физический эфир, в котором и локализованы все материальные объекты (тела и поля), взаимодействуя между собой по установленным законам. При этом за размерность мира мы вправе принимать число независимых свойств данного мира, то есть число его атрибутов, присущих ему по определению. Здесь уместно вспомнить, что ДЕФОНОМ является окрестность деформированной среды вокруг ЛОКАЛЬНОЙ ДЕФОРМАЦИИ в точке О с указанными компонентами нормальных и тангенциальных напряжений. Ясно, что субстанция в мире деформаций обладает физическими свойствами, близкими к свойствам физического вакуума, примерные представления о которых мы имеем по результатам инструментальных исследований ближнего космического пространства: температура близка к абсолютному нулю, вязкость соответствует сверхтекучести при сверхнизких температурах и т. п.

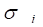
При этом из известного в геометрии свойства совместности деформаций ясно, что плотность субстанции в таком ДЕФОНЕ сжатия больше плотности субстанции в его окрестности, что Рис. 1мы графически представили некоторой зависимостью.

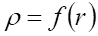
(1),.

где от точки О, как это показано на рис. 1.

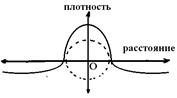
Рис. 1.

Известно, что понятие НАПРАВЛЕНИЯ в ГЕОМЕТРИИ определяется величиной УГЛА — величины, которая появляется лишь в двумерных мирах — поверхностях (радиан) и в трёхмерных мирах (стерадиан). При этом, если для если для однозначности величины плоского УГЛА необходимо указание его знака (правый — по часовой стрелке или левый — против часовой стрелки относительно заданного РЕПЕРА — линии), то для однозначности величины УГЛА пространственного ещё необходимо указание и его ориентации относительно поверхности. Для иллюстрации отмеченного обстоятельства воспользуемся результатами топологических исследований векторных полей на поверхностях [3] и др. Представим себе простейший такой сфероидный ДЕФОН сжатия в окрестности точки О как на рис. 2, тогда на рис. 3 получим изображение векторных полей нормальных (рис. 3-а) и тангенциальных (рис. 3-б) компонент напряжения в смежной со сфероидом окрестности, которые по определению ортогональны друг другу.

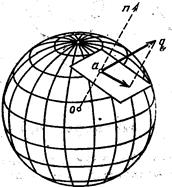
Рис. 2.

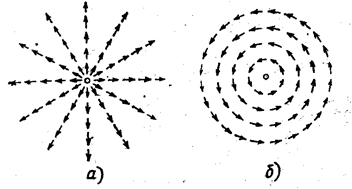
Рис. 3.

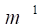
Вместе с этим, два подобных ДЕФОНА, расположенные вблизи друг от друга, окажутся с противоположных сторон любой поверхности, которые всегда могут быть представлены замкнутыми в бесконечности по несобственной линии вокруг любого из ДЕФОНОВ, как это наглядно показано на рис. 4, на котором — след пограничной поверхности между окрестностями ДЕФОНОВ и, имеющих характеристики и соответственно.

Как это мы уже отмечали ранее [1], радиус кривизны этой поверхности для ДЕФОНОВ и будет иметь противоположные знаки. Из отмеченных обстоятельств сразу следует необходимость сближения двух соседних таких ДЕФОНОВ — СФЕРОИДОВ сжатия, что равнозначно притяжению, как это показано на рис. 4.

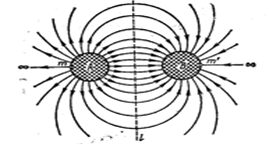
Рис. 4.

Как мы установили ранее [1], такая поверхность может принимать один из показанных на рис. 5 (сфера), рис. 6 (тор) и рис. 7 (скрученный тор) видов:

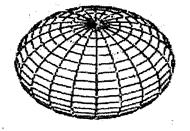
Рис. 5.

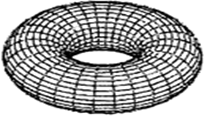
Рис. 6.

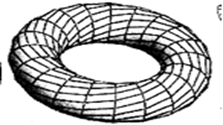
Рис. 7.

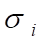
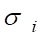
Из одного того факта, что в отличие от односвязного сфероида тороид (см. рис.6) является двухсвязным [1], сразу следует вывод об отсутствии центральной симметрии векторного поля нормальных компонент напряжения, присущих сфероиду, приобретая в полярной плоскости, ортогональной экваториальной плоскости тороида, осевую симметрию, позволяя представить изменение векторного поля нормальных компонент напряжения, опуская математические преобразования, проделанные автором ранее [4], как на рис. 8, на котором обозначены штриховыми линиями n иn предельные уровни значений векторного поля нормальных компонент напряжения.

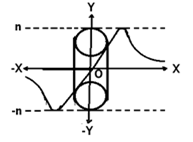
Рис. 8.

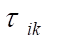
Из отмеченных обстоятельств снова следует вывод о необходимости сближения двух соседних таких ДЕФОНОВ-ТОРОИДОВ сжатия, что равнозначно притяжению, подобно притяжению ДЕФОНОВ-СФЕРОИДОВ на рис. 13, но величина такого тяготения ДЕФОНОВ-ТОРОИДОВ находится в зависимости не только от расстояния между ними, но и от относительной друг друга пространственной ориентации: в экваториальных плоскостях их взаимодействие подчиняется центральной симметрии, подобно взаимодействия ДЕФОНОВ — СФЕРОИДОВ (см. рис.4), а в полярной плоскости взаимодействие ДЕФОНОВ-ТОРОИДОВ сжатия подчиняется осевой симметрии, также здесь оставляя пока вопрос о величине такого тяготения открытым. При этом здесь важно отметить действие отмеченной особенности взаимодействия ДЕФОНОВ-ТОРОИДОВ в отличие взаимодействия ДЕФОНОВ — СФЕРОИДОВ лишь, как это ясно из графической зависимости на рис. 8, на расстояниях между ДЕФОНАМИ-ТОРОИДАМИ, сравнимыми с их собственными размерами. Кроме того нам известно [1], что окрестность деформированной среды вокруг ЛОКАЛЬНОЙ ДЕФОРМАЦИИ в точке О с указанными компонентами нормальных и тангенциальных напряжений, ограниченная поверхностью, образует ДЕФОНЫ — СФЕРОИДЫ и ДЕФОНЫ — ТОРОИДЫ, которые в свою очередь образуют асимметричные СКОБЫ, в окрестностях которых сопутствующие деформации создают также асимметричные области, в пределах которой значения и направления нормальных и тангенциальных компонент напряжения отображают эту асимметричность окрестностей с различных сторон относительно СКОБЫ СКРУЧЕННОГО ДЕФОНА-ТОРОИДА. Также, учитывая обстоятельство, что понятие НАПРАВЛЕНИЯ в ГЕОМЕТРИИ определяется величиной и знаком УГЛА, приходится признать определяющее влияние на величину и направление взаимодействия также и НАПРАВЛЕНИЯ КРУЧЕНИЯ СКРУЧЕННЫХ ДЕФОНОВ-ТОРОИДОВ, которых может быть два: ПРАВОЕ или ЛЕВОЕ. В действительности образование ДЕФОНА-СКРУЧЕННОГО ТОРОИДА возможно представить как процесс движения окружности вокруг некоторой точки деформируемой среды по внешней оси — замкнутой траектории при вращении этой окружности относительно траектории движения центра этой окружности до замыкания траектории — являющейся осью ТОРОИДА. Как мы видели выше [1], деформации кручения сопутствуют все остальные виды деформации: и сжатие, и растяжение, и сдвиг, и изгиб. Поэтому особый практический интерес для нас представляет та зависимость.

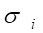
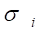
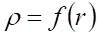
(1).

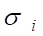
плотности от расстояния внутри самого ДЕФОНА-СКРУЧЕННОГО ТОРОИДА и в его окрестностях, как это нами было установлено для ДЕФОНА — СФЕРОИДА (см. рис. 1), и также зависимость векторного поля нормальных компонент напряжения в его окрестности, как это мы выше обнаружили для ДЕФОНА-ТОРОИДА.

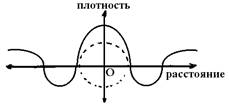
Рис. 9.

В соответствии с отмеченными «УСЛОВИЯМИ СОВМЕСТНОСТИ ДЕФОРМАЦИЙ» Сен-Венана [1] совершенно понятно, что при кручении ДЕФОНА-ТОРОИДА его поверхностный слой испытывает растяжение, которое при необходимости можно даже вычислить, сравнив длины винтовой линии с длиной соответствующего экватора тороида. Данное обстоятельство приводит к необходимости деформации растяжения в ближайшей СКРУЧЕННОМУ ДЕФОНУ-ТОРОИДУ окрестности как рис. 9.

стереохронодинамика дефон сфероид тороид.