Фазовая плоскость и фазовое пространство

Фазовая плоскость и фазовое пространство геометрические инструменты изучения автономных систем. Для простоты мы будем говорить о системе второго порядка

и фазовой плоскости, случай же системы более высокой размерности п и соответствующего n-мерного фазового пространства мы оставляем для самостоятельного обобщения.

В основе понятия фазовой плоскости лежит достаточно простое соображение: геометрически решение системы (23.1) можно изобразить кривой в трехмерном пространстве (t, x, y), определяемой соотношениями х = x (t), y = y{t) (это будет график решения), а можно воспользоваться парой функций x (t), y (t) и по-другому, проинтерпретировав ее как закон движения точки (х, у) по плоскости. На плоскости геометрическим образом решения является множество {(x (t), y (t)), t Е Ж} кривая, заданная параметрически, которую обычно называют траекторией* точки, движущейся по закону (x (t), y (t)).

Определение 23.2 Переменные х и у, фигурирующие в системе (23.1), называют фазовыми переменными^[1][2], плоскость (х, у) фазовой плоскостью, вектор {х, у) фазовой скоростью, траекторию решения (x (t), y (t)) ф, а з о, а о й т р, а е к т о р и е й.

Основным геометрическим эффектом, который делает фазовую плоскость исключительно универсальным инструментом, является то. что различные фазовые траектории не пересекаются друг с другом.

Лемма 23.1 Две фазовые траектории либо не пересекаются, либо совпадают.

Доказательство состоит в фиксации следующих трех фактов. Вопервых, если (x (t), y (t)) решение системы (23.1). то для любого, а решением системы будет и (x (t + a), y (t + a)). Действительно, подстановка этих функций в систему дает тождества:

и аналогично для второго уравнения.

Во-вторых, решениям, отличающимся сдвигом аргумента, отвечает одна и та же траектория: точка, на которой одно решение оказывается в момент времени t, проходится и другим решением, но только в другой момент, отличающийся от t на а. Грубо говоря, они проходят по одному и тому же пути, но одно раньше, а другое позже.

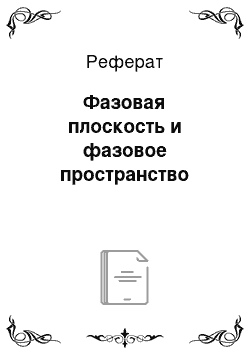
И, наконец, в-третьих, если траектории двух решений (x (t), y (t)) и (x2(t), jj2{t)) пересеклись в точке (х*, у*). то это означает, что для некоторых моментов времени t и t2 выполнено.

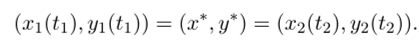
Если t = 12, то два указанных решения обязаны просто совпадать в силу теоремы существования и единственности они удовлетворяют одному и тому же начальному условию. Если же t ф t2, то (x (t), yi (t)) по той же причине совпадает уже со сдвигом второго решения на ^ — t: (X2(t + t2 — 11), y2(t + t2~ ti)), и в этом случае первое и второе решения также порождают одну и ту же траекторию. Лемма доказана.

Следствие. Если траектория имеет самопересечения, то есть для некоторых t ф t2 выполнено (x (t), y (t)) — (x (t2), y (t2)), то решение периодическое.

Действительно, решение (x (t + t2 — t), y (t + t2 — ii)) при t = t совпадает с решением (x (t), y (t)), а значит, они совпадают всюду. Если обозначить и> = t2 — t, то мы получим как раз условие периодичности: (x (t+ui), y (t+u))) = (x (t), y (t)). Траектория при этом представляет из себя замкнутую кривую: возвратившись через период ш в исходную точку, решение снова повторяет свой путь по этой же траектории. Замкнутые траектории на фазовой плоскости обычно называют циклами.

Определение 23.3 Совокупность фановых траекторий называют {(> а з о в ы м п о р гп р е т о м. системы.

Самым замечательным является то. что фазовый портрет иногда можно построить, не решая систему: уравнение фазовых траекторий получается просто делением второго уравнения системы (23.1) на первое, так что нам надо решить только дифференциальное уравнение первого порядка (или, но крайней мере, исследовать, как ведут себя его решения):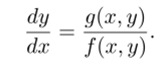

• [1] 'Траектория есть, но существу, проекция графика в пространстве (t, x, y) на плоскость (х, у).
• [2] Термин «фазовый11 происходит из традиции описания периодических движенийв терминах фазы положения относительно начала периода (сравните, например, свыражением «фазы Луны11). Позднее он укоренился в электротехнике, где работают, как правило, гармонические колебания (вида A cos (ujt + ф)), для которых под «фазой11 понимается аргумент у косинуса. В электротехническом жаргоне под «фазой11понимают провод, на который подается напряжение (обычно синусоидальное). Здесьже родилось выражение «сдвиг фазы11 или «сдвиг по фазе11, которое теперь сталообщеупотребительным жаргоном, но обозначающим совершенно далекие от периодических процессов веши. Таким образом, термин «фазовая переменная11 означаеттолько то, что переменная меняется по периодическому закону. Использование фазовой плоскости (т.е. плоскости фазовых переменных) оказалось крайне эффективнымдля анализа различных периодических процессов, главным образом нелинейных. Нуа употребление прилагательного «фазовый11 дли произвольной автономной системыэто уже мутация термина, связанная с поднятием приемов, использовавшихся ванализе колебательных процессов, на более высокий уровень общности. Вместе сприемами и методами гуда «переезжают11 и их названии, зачастую отрываясь от своего изначального смысла.