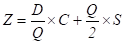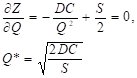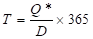Управление запасами в условиях зависимого спроса. 
Базовая и интервальная варианты модели АНМ

Базовая модель АНМ.

Оптимизации подлежит объем партии поставки, а следовательно количество поставок в год и интервал между поставками.

Ограничения модели:

• -стоимость материалов не зависит от объема закупки
• -дефицит материала недопустим
• — потребность в материале заранее известна и постоянна во времени
• — поставка возможна в любое время

Введем условные обозначения:

— суммарные годовые затраты, связанные со снабжением;

• — годовая потребность в материале
• — затраты хранения единицы среднегодового запаса;
• — оптимальный объем одной поставки.

Суммарные затраты, подлежащие оптимизации, включают затраты на заказ и на хранение:

.

DC/Q — годовые затраты на заказ (D/Q — количество поставок за год).

Q/2- средние годовые остатки на складах; Q — максимальное количество товара на складе в момент поставки, в течение Интервала между поставками оно равномерно расходуется до нуля, следовательно средний остаток составит половину от Q.

Продифференцировав формулу по Q и приравняв к нулю, получим искомую величину оптимальной партии поставки:

Интервал между двумя поставками T (в днях) рассчитывается по формуле:

где 365 -количество дней в году.

В случае, если начальные условия модели не выполняются возможно использование интервальных моделей.

Примеры применимости интервальной модели.

• 1. Цена дискретно зависит от объема одной поставки
• 2. В зависимости от Q изменяются затраты на 1 заказ (например, для транспортировки партии выше определенной требуется аренда более вместительного транспортного средства)
• 3. В зависимости от Q изменяются затраты на содержание запасов (например, если уровень запасов больше вместимости собственного склада, используется арендуемый склад с большими затратами).

Последовательность оптимизации такова:

• — выделяют интервалы значения Q, для каждого из которых будут выполняться все условия базовой модели
• — рассчитывается оптимальный объем партии поставки Q* для каждого интервала
• — если оптимальный объем Q* попадает в интервал, он принимается в качестве варианта решения, если не попадает — в качестве варианта рассматривается граница интервала.
• — для всех вариантов решения рассчитываются совокупные издержки. Такой расчет будет произведен по всем интервалам. Выбирают вариант, дающий минимальные совокупные издержки.