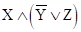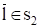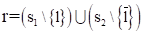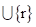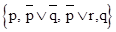Принцип резолюций в логике высказываний

Не существует общего, по-настоящему эффективного критерия для проверки выполнимости КНФ (Конъюнктивной Нормальной Формы). Тем не менее, есть достаточно удобный метод для выявления невыполнимости множества дизъюнктов. Действительно, множество дизъюнктов невыполнимо тогда и только тогда, когда пустой дизъюнкт? является логическим следствием из него. Таким образом, невыполнимость множества S можно проверить, порождая логические следствия из S до тех пор, пока не получим пустой дизъюнкт.

Для порождения логических следствий будет использоваться очень простая схема рассуждений. Пусть A, B и X — формулы. Предположим, что две формулы () и () — истинны. Если Х тоже истинна, то отсюда можно заключить, что В истинна. Наоборот, если Х ложна, то можно заключить, что, А истинна. В обоих случаях () истинна. Получается правило:

|=.

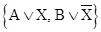
которое можно записать также в виде:

|=.

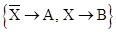
В том частном случае, когда Х — высказывание, а, А и В — дизъюнкты, это правило называется правилом резолюций.

Например, из дизъюнктов и выводим дизъюнкты. Обратим внимание на то, что в первых двух дизъюнктах есть еще одна пара противоположных литералов. Условимся, что можно применять правило резолюций не обязательно к самым левым литералам (поскольку мы не различаем дизъюнкты, отличающиеся порядком записи литералов). Тогда правило резолюций, примененное к Y и, даст .

Выводом из S называется последовательность дизъюнктов D, D₂,…, D_n такая, что каждый дизъюнкт этой последовательности принадлежит S или следует из предыдущих по правилу резолюций. Дизъюнкт D выводим из S, если существует вывод из S, последним дизъюнктом которого является D.

Например, если.

S={,, X},.

то последовательность.

D₁=, D₂=, D₃=, D₄=X, D₅=.

— вывод из S. Дизъюнкт выводим из S.

Применение метода резолюций основано на следующем утверждении, которое называется теоремой о полноте метода резолюций.

Теорема. Множество дизъюнктов логики высказываний S невыполнимо тогда и только тогда, когда из S выводим пустой дизъюнкт.

Доказательство.

Докажем вначале достаточность. Отметим, что правило резолюций сохраняет истинность. Это означает, что если j ()=1 и j ()=1 для некоторой интерпретации j, то j ()=1. Действительно, пусть j ()=1 и j ()=1. Тогда если j (F)=1, то и j ()=1. Если же j (F)=0, то j (ШX)=1, поскольку j ()=1. Но в этом случае j (X)=0 и j (G)=1, так как j ()=1. Если же j (G)=1, то и j ()=1.

Пусть из S выводим пустой дизъюнкт. Предположим противное: множество S выполнимо, т. е. существует интерпретация y, при которой все дизъюнкты из S истинны. Выводимость пустого дизъюнкта из S означает, что существует последовательность дизъюнктов D₁,…, D_n=?, каждый дизъюнкт которой принадлежит S или получается из предыдущих по правилу резолюций. Если дизъюнкт D_j из этой последовательности принадлежит S, то по предположению y (D_j)=1. Если же он получается из предыдущих по правилу резолюций, то также y (D_j)=1, поскольку правило резолюций сохраняет истинность. При i=n получаем, что y (?)=1. Противоречие показывает, что предположение о выполнимости множества S — ложное предположение. Следовательно, S невыполнимо. Достаточность доказана.

Докажем необходимость. Доказательство проведем индукцией по следующему параметру: d (S)=сумма числа вхождений литералов в дизъюнкты из S минус число дизъюнктов.

Пусть множество дизъюнктов S невыполнимо. Если пустой дизъюнкт принадлежит S, то он выводим из S (вывод в этом случае состоит из одного пустого дизъюнкта) и необходимость теоремы доказана. Будем считать в силу этого, что? S. При этом предположении каждый дизъюнкт содержит хотя бы один литерал и поэтому dі1.

База индукции: d (S)=1. Если d (S)=1, то все дизъюнкты состоят из одного литерала. Поскольку множество S невыполнимо, то в нем должна найтись пара противоположных литералов X и. В таком случае пустой дизъюнкт выводим из S, соответствующий вывод содержит три дизъюнкта: X, ,.

Шаг индукции: d (S)>1. Предположим, что для любого множества дизъюнктов Т такого, что d (Т).

Пусть.

S={D₁, D₂,…, D_k-1, D_k}.

Так как d (S)>1, то в S существует хотя бы один неодноэлементный дизъюнкт. Будем считать, что это дизъюнкт D_k, т. е. D_k=LD_k?, где L — литерал и D_k?№?. Наряду с множеством дизъюнктов S рассмотрим еще два множества дизъюнктов.

S₁={D₁, D₂,…, D _k-1, L},.

S₂={D₁, D₂,…, D_k-1, D_kґ}.

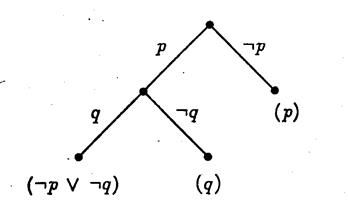
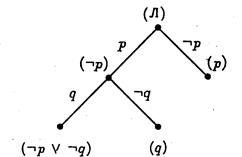
Ясно, что S₁ и S₂ невыполнимы и что d (S₁)₂)₁ и S₂ выводим пустой дизъюнкт.

Пусть A₁, A₂,…, A_i,…, A_l-1, A_l=? — вывод пустого дизъюнкта из S₁ и B₁, B₂,…, B_j,…B_m-1, B_m=? — вывод пустого дизъюнкта из S_2. Если в первом выводе не содержится дизъюнкта L, то эта последовательность дизъюнктов будет выводом из S и необходимость теоремы доказана. Будем считать, что L содержится в первом выводе, пусть A_i=L. Аналогично предполагаем, что B_j=D_k?.

Если дизъюнкт Е получается из дизъюнктов Е₁ и Е₂ по правилу резолюций, то будем говорить, что Е непосредственно зависит от Е₁ (и от Е₂). Транзитивное замыкание отношения непосредственной зависимости назовем отношением зависимости (Другими словами, E зависит от Еґ, если существуют дизъюнкты Е₁,…, Е_2n такие, что E=E₁,…, E_n=Eґ_ и Е₁ непосредственно зависит от Е₂,…, E_n-1 непосредственно зависит от E_n). Преобразуем второй вывод следующим образом: к дизъюнкту B_j и всем дизъюнктам, которые от него зависят, добавим литерал L. Новая последовательность дизъюнктов B₁, B₂,…, B_jґ= D_kґL, Bґ_j+1,…, B_mґ (*) будет выводом из S. Если дизъюнкт B_m не зависит от B_j, то B_mґ =?. Это означает, что из S выводим пустой дизъюнкт, и необходимость теоремы доказана. Предположим, что B_m зависит от B_j. Тогда B_mґ=L. Преобразуем теперь первый вывод: на место дизъюнкта A_i (равного L) в этой последовательности подставили последовательность (*). Получим последовательность.

A₁,…, A_i-1, B_1,…, Bґ, Bґ_j+1,…, B _mґ=L, A _i+1,…, A _l=?.

Эта последовательность является выводом пустого дизъюнкта из множества дизъюнктов S. Следовательно, если множество S невыполнимо, то из S выводим пустой дизъюнкт.

Теорема доказана.

Для доказательства того, что формула G является логическим следствием множества формул F₁,…, F_k метод резолюций применяется следующим образом. Сначала составляется множество формул T={F₁,…, F_k, }. Затем каждая из этих формул приводится к конъюнктивной нормальной форме и в полученных формулах зачеркиваются знаки конъюнкции. Получается множество дизъюнктов S. И, наконец, ищется вывод пустого дизъюнкта из S. Если пустой дизъюнкт выводим из S, то формула G является логическим следствием формул F₁,…, F_k. Если из S нельзя вывести ?, то G не является логическим следствием формул F₁,…, F_k.

Проиллюстрируем сказанное на примере. Покажем, что формула G=Z является логическим следствием формул F₁=, F₂=. Сформируем множество формул T={F₁, F₂, }. Приведем формулы F₁ и F₂ к КНФ (формула сама имеет эту форму). Мы получим, что F₁ равносильна, F₂ равносильна (YZ).

Тогда множество дизъюнктов S равно {X,, YZ, }.

Из множества S легко выводится пустой дизъюнкт:, ,, YZ, Y, ?.

Следовательно, формула G является логическим следствием формул F₁, и F₂.

Общезначимость правила резолюций выражается следующей леммой.

Лемма (1). Пусть s₁ и s₂ — дизъюнкты нормальной формы S, l — литера. Если и, то дизъюнкт является логическим следствием нормальной формы S. (Дизъюнкт r называется резольвентой дизъюнктов s₁ и s₂).

Следствие. Нормальные формы S и S эквивалентны.

Доказательства невыполнимости, основанные на принципе резолюций Доказательства невыполнимости логических формул очень важны в ИИ (Искусственный Интеллект). Способы таких доказательств, основанные на принципе резолюций, выделяются среди прочих тем, что они дают возможность использовать средства автоматического доказательства, применяемые в логическом программировании.

При всей простоте метод резолюций (или, короче, резолюция) достаточен для обнаружения возможной невыполнимости множества приведённых дизъюнктов. Таким образом, можно попробовать доказать невыполнимость конечного множества дизъюнктов из S с помощью следующего алгоритма.

При условии, что? S:

• 1)выбираем l, s₁ и s₂, такие что и ;
• 2) вычисляем резольвенту r;
• 3) заменяем S на S.

В качестве примера проверим невыполнимость множества.

S=.

Дизъюнкты удобно пронумеровать, получится следующий список:

• 1.
• 2.
• 3.
• 4.

Затем вычисляются и добавляются к S резольвенты. В списке, который приводится ниже, каждый дизъюнкт — резольвента некоторых из предшествующих дизъюнктов. Номера их приведены в скобках справа от соответствующей резольвенты.

• 5. (1,3)
• 6. (1,4)
• 7. (2,3)
• 8. (2,4)
• 9. (2,5)
• 10. (3,6)
• 11. (3,8)
• 12. (4,5)
• 13. (4,7)
• 14.? (4,9)

Замечание. Алгоритм проверки невыполнимости — недетерминированный, вообще говоря, возможен не один выбор для l, s₁ и s_2. В приведённом примере мы выбирали дизъюнкты s₁ и s₂ в лексикографическом порядке номеров. Такая стратегия неоптимальна. Некоторые резольвенты оказались ненужными, а также вычислялись в некоторых случаях более одного раза. Для сравнения продемонстрируем теперь применение этого же алгоритма с минимумом резолюций:

• 5. (1,4)
• 6. (2,4)
• 7. (3,6)
• 8.? (5,7)

Ясно, что принятая стратегия может значительно влиять на процесс выполнения алгоритма. Тем не менее упомянем два важных свойства, не зависящих от используемой стратегии.

Прежде всего, если множество S не содержит ни одной пары дизъюнктов, допускающих резольвенту, то оно выполнимо (разумеется, за исключением случая, когда оно содержит пустой дизъюнкт). Интерпретация I получается заданием l (p)=И тогда и только тогда, когда положительная литера p принадлежит одному из дизъюнктов множества S.

Во-вторых, если выполнение этого алгоритма закончилось «нормально» после порождения пустого дизъюнкта, то установлена невыполнимость исходного множества S. Это непосредственное следствие леммы 1.

Может случиться, что выполнение алгоритма не завершится, хотя число различных дизъюнктов, которые могут быть порождены с помощью резолюций, очевидно, конечно. Например, такое явление имеет место для множества. Резольвентный дизъюнкт q будет порождаться неограниченное число раз. Рассмотрим также случай невыполнимого множества. Оптимальная стратегия установит невыполнимость посредством построения резольвент q, а затем ?. Напротив, «неадекватная» стратегия приведёт к зацикливанию, которое только что было отмечено. Таким образом, можно констатировать, что стратегия влияет не только на эффективность алгоритма, но и на его завершаемость.

Представляет интерес свойство завершаемости метода резолюций: конечное множество S невыполнимо тогда и только тогда, когда пустой дизъюнкт может быть выведен из S с помощью резолюций. Из леммы 1 следует достаточность этого условия. Пустой дизъюнкт, будучи невыполнимым, не может быть логическим следствием из выполнимого множества дизъюнктов. Необходимость сформулированного условия приведена в следующей лемме.

Лемма (2). Если множество дизъюнктов S невыполнимо и содержит резольвенты своих элементов, то оно обязательно содержит пустой дизъюнкт.

Число различных дизъюнктов, которые можно составить на основе конечного множества S, конечно. Таким образом, лемма 2 лаёт простое общее средство решения вопроса о выполнимости или невыполнимости конечного множества дизъюнктов.

Проиллюстрируем лемму одним очень простым примером. Рассмотрим множество дизъюнктов S=. Первый этап состоит в построении семантического дерева и помечивании каждого листа дизъюнктом, делающим ложной интерпретацию, соответствующую этому листу. Это возможно тогда и только тогда, когда S невыполнимо. Здесь именно такой случай и подходящее дерево изображено на рисунке 1.

Рис. 1.

Второй этап состоит в том, что каждому узлу N дерева сопоставляется некоторый дизъюнкт с. Этот дизъюнкт будет зависеть од дизъюнктов с₁ и с_2, которые уже сопоставлены двум узлам, следующим за N. Две соответствующие дуги помечены двумя противоположными литерами, скажем и. Если один из дизъюнктов, например с₁ не содержит ни, ни её отрицание, то можно выбрать с= с₁, в противном случае с будет резольвентой для с₁ и с₂ по отношению к. Этот результат, полученный для множества S, иллюстрируется рисунком 2.

Рис. 2.

Заметим, что каждый узел помечен дизъюнктом, при котором ложна частичная интерпретация, соответствующая этому узлу. Таким образом, корень будет помечен пустым дизъюнктом. Наконец, по построению каждый дизъюнкт является элементом S или получен из S с помощью резолюции. Число резольвент, которые надо вычислить для установления невыполнимости множества дизъюнктов S, не больше числа невисячих узлов семантического дерева. Максимальное значение этой величины равно, где n-число различных высказываний, входящих в S. Тем самым показано, что резолюция неэффективна, если применяется только что описанная простая стратегия. Отметим, что некоторые стратегии выбора приводят к лучшим реализациям.

Лемма 2 остаётся справедливой для бесконечного S. Отсюда следует, что бесконечное множество дизъюнктов невыполнимо тогда и только тогда, когда в нём найдётся конечное невыполнимое подмножество. Приведём непосредственное следствие, отражающее свойство завершаемости принципа резолюции.

Следствие. Если множество S формул невыполнимо, то этот факт всегда можно установить методом резолюций.