Теоремы сравнения для положительных рядов

Теорема (признак сравнения). Пусть даны два ряда с неотрицательными членами.

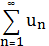
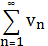
(3) (4).

И пусть существует номер такой, что для любого n выполняются неравенства, тогда из сходимости ряда (4) следует сходимость ряда (3), а из расходимости ряда (3) следует расходимость ряда (3).

Пусть даны два знакоположительных ряда:

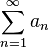
и.

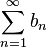
Тогда, если, начиная с некоторого места (), выполняется неравенство:

.

то из сходимости ряда следует сходимость .

Или же, если ряд расходится, то расходится и .

Доказательство Обозначим частные суммы ряда. Из неравенств следует, что Поэтому из ограниченности вытекает ограниченность, а из неограниченности следует неограниченность Справедливость признака вытекает из критерия сходимости для.

Признак сравнения отношений Также признак сравнения можно сформулировать в более удобной форме — в виде отношений.

Формулировка Если для членов строго положительных рядов и, начиная с некоторого места (), выполняется неравенство:

.

то из сходимости ряда следует сходимость, а из расходимости следует расходимость .

Доказательство Перемножая неравенства, составленные для, получаем.

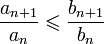
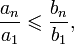
или.

Дальше достаточно применить признак сравнения для положительных рядов и.

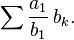
Предельный признак сравнения Поскольку достоверно установить справедливость этого неравенства при любых n — довольно сложная задача, то на практике признак сравнения обычно используется в предельной форме.

Формулировка Если и есть строго положительные ряды и.

.

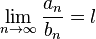
то при из сходимости следует сходимость, а при из расходимости следует расходимость .

Доказательство Если то для достаточно больших.

Из ограниченности частных сумм следует ограниченность частных сумм Соотношения обеспечивают на основании признака сравнения сходимость и вместе с тем сходимость Если же то и не может сходиться при расходящемся.

Признак Даламбера.

Примзнак д’Аламбемра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.

Если для числового ряда.

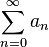
существует такое число, , что начиная с некоторого номера выполняется неравенство.

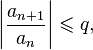
то данный ряд абсолютно сходится; если же, начиная с некоторого номера.

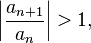
то ряд расходится.

Признак сходимости д’Аламбера в предельной форме Если существует предел.

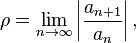
то рассматриваемый ряд абсолютно сходится если, а если — расходится.

Замечание. Если, то признак д? Аламбера не даёт ответа на вопрос о сходимости ряда.

Доказательство.

тогда существует, существует, для любого .

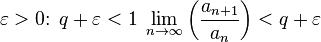
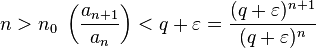
Ряд из сходится (как геометрическая прогрессия). Значит, ряд из сходится (по признаку сравнения).

1., тогда существует .

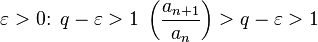
2. для любого. Тогда не стремится к нулю и ряд расходится.

Радикальный признак Коши.

Радикальный признак Коши — признак сходимости числового ряда:

Если для числового ряда с неотрицательными членами существует такое число, , что, начиная с некоторого номера, выполняется неравенство, то данный ряд сходится.

Предельная форма Условие радикального признака равносильно следующему:

То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:

Если для ряда.

то.

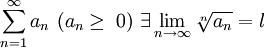
если ряд сходится, если ряд расходится, если вопрос о сходимости ряда остается открытым.

Доказательство.

1. Пусть. Очевидно, что существует такое, что. Поскольку существует предел, то, подставив в определение предела выбранное, получим:

Раскрыв модуль, получаем:

Поскольку, то ряд сходится. Следовательно, по признаку сравнения ряд тоже сходится.

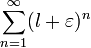
2. Пусть. Очевидно, что существует такое, что. Поскольку существует предел, то, подставив в определение предела выбранное, получим:

Раскрыв модуль, получаем:

Поскольку, то ряд расходится. Следовательно, по признаку сравнения ряд тоже расходится.

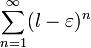
Интегральный признак Коши.

Формулировка теоремы Пусть для функции f (x) выполняется:

• 1. (функция принимает неотрицательные значения)
• 2. (функция монотонно убывает)
• 3. (соответствие функции ряду)

Тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

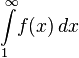
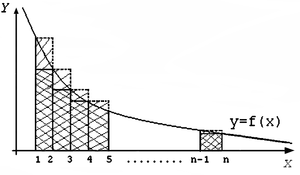
Рис. 1 Набросок доказательства

• 1. Построим на графике f (x) ступенчатые фигуры как показано на рисунке
• 2. Площадь большей фигуры равна
• 3. Площадь меньшей фигуры равна
• 4. Площадь криволинейной трапеции под графиком функции равна

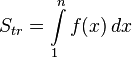
5. Получаем.

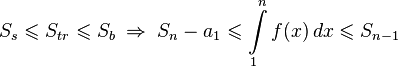
6. Далее доказывается с помощью критерия сходимости знакоположительных рядов.