Теоретическая часть. 
Производственная функция как модель процесса производства

Понятие производственной функции

Производственная функция — это функция, независимая переменная которой принимает значения объёмов затрачиваемого или используемого ресурса (фактора производства), а зависимая переменная — значения объёмов выпускаемой продукции.

(1).

В формуле (1) и — числовые величины, т. е. есть функция одной переменной. В связи с этим ПФ называется одно ресурсной или однофакторной ПФ, её область определения — множество неотрицательных действительных чисел (т. е.). Запись означает, что если ресурс затрачивается или используется в количестве единиц, то продукция выпускается в количестве единиц. Символ — знак функции — является характеристикой производственной системы, преобразующей ресурс в выпуск. Символ связывает между собой независимую переменную с зависимой переменной. В макроэкономической теории принято считать, что — это максимально возможный объём выпуска продукции, если ресурс затрачивается или используется в количестве единиц. В макроэкономике такое понимание не совсем корректно: возможно, при другом распределении ресурсов между структурными единицами экономики выпуск мог бы быть и большим. В этом случае ПФ — это статистически устойчивая связь между затратами ресурса и выпуском. Более правильной является символика, где — вектор параметров ПФ.

ПФ могут иметь различные области использования. Принцип «затраты — выпуск» может быть реализован как на микро — так и на макроэкономическом уровне. Сначала остановимся на микроэкономическом уровне. ПФ может быть использована для описания взаимосвязи между величиной затрачиваемого или используемого ресурса в течение года на отдельном предприятии и годовым выпуском продукции этого предприятия. На микроэкономическом уровне в роли производственной системы может выступать также отрасль, межотраслевой производственный комплекс. МИПФ строятся и используются в основном для решения задач анализа и планирования, а также задач прогнозирования.

ПФ может быть использована для описания взаимосвязи между годовыми затратами труда в масштабе региона или страны в целом и годовым конечным выпуском продукции (или доходом) этого региона или страны в целом. Здесь в роли производственной системы выступает регион или страна в целом (точнее хозяйственная система региона или страны) — имеем макроэкономический уровень и макроэкономическую ПФ (МАПФ). МАПФ строятся и активно используются для решения всех трёх типов задач (анализа, планирования и прогнозирования).

Точное толкование понятий затрачиваемого (или используемого) ресурса и выпускаемой продукции, а также выбор единиц их измерения зависят от характера и масштаба производственной системы, особенностей решаемых (с помощью ПФ) задач (аналитических, плановых, прогнозных), наличия исходных данных. На микроэкономическом уровне затраты и выпуск могут измеряться как в натуральных, так и в стоимостных единицах (показателях). Годовые затраты труда могут быть измерены в человеко-часах (объём человеко-часов — натуральный показатель) или в рублях выплаченной заработной платы (её величина — стоимостной показатель). Выпуск продукции может быть представлен в штуках или в других натуральных единицах (тоннах, метрах и т. п.) или в виде своей стоимости.

На макроэкономическом уровне затраты и выпуск измеряются, как правило, в стоимостных показателях и представляют собой стоимостные (ценностные) агрегаты, т. е. суммарные величины произведений объёмов затрачиваемых (или используемых) ресурсов и выпускаемых продуктов на их цены. Производственная функция (ПФ) — это модель, которая выражает технологическую зависимость между результатами деятельности технического объекта и затратами факторов производства. Входными параметрами являются ресурсы R₁, …, R_n, а выходными — результат в виде годовых объемов производства различных видов продукции Y₁, …, Y_m .

В качестве ресурсов (факторов производства) наиболее часто рассматриваются величины затрат живого труда, предметов и средств труда, используемых в процессе производства: накопленный труд в форме производственных фондов (капитал) К и настоящий (живой) труд. В качестве результата рассматривается валовой выпуск (либо валовой внутренний продукт, либо национальный доход).

Простейшей моделью производственной функции является:

Y — выход;

K — капитал;

L — трудовые ресурсы.

Таким образом, экономика замещается своей моделью в форме ПФ.

Y= F (K, L),.

т.е. выпуск (продукции) есть функция от затрат ресурсов (капитала и труда). производственный предельный модель Если модель учитывает время t затрат на производство, то производственная функция записывается в виде:

Y = F (K, L, t).

Производственная функция должна удовлетворять следующим условиям, поддающимся естественной экономической интерпретации:

• 1) F (K, L) — непрерывная дважды дифференцируемая функция в области K>0;
• 2) ,

с ростом ресурсов выпуск растет;

3) ,.

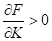
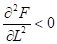
с увеличением ресурсов скорость роста выпуска замедляется;

Темпы прироста часто убывают при увеличении какого-либо фактора, особенно, если производство ведется по какой-либо неизменной технологии. Убывание темпов роста при увеличении масштабов производства часто связано с вынужденным использованием более дорогих или менее качественных ресурсов. При этом при достижении определенного уровня инвестиций в производство какого-нибудь отдельного фактора рост производства прекращается полностью, несмотря на увеличение рассматриваемого фактора.

• 4) F (K, L) = F (K, L)
• — гипотеза однородности
• 5) F (0, L) = F (K, 0) = 0
• — при отсутствии одного из ресурсов производство невозможно;

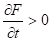
6) для F (K, L, t).

Виды производственных функций Рассмотрим 4 производственные функции:

1. Линейная модель (функция с взаимозамещением ресурсов), задается уравнением:

Y = a₀ + b₁K + c₁L,.

где b₁, c₁ >0 — частные эффективности ресурсов (предельный физический продукт затрат).

2. Квадратичная модель, задается уравнением:

Y = a₀ + b₁K + c₁L + b₂K² + c₂L²

3. Модель Кобба-Дугласа, задается уравнением:

Y = AKL,.

где, А — коэффициент нейтрального технического прогресса; а₁, a₂ -коэффициенты эластичности по труду и капиталу.

4. Модель с учетом НТП, задается уравнением:

Y = AKLe^0t,.

где — специальный множитель технического процесса, 0 — параметр нейтрального НТП (0 >0).

Параметры функции могут быть определены по методу наименьших квадратов.

1. Для линейной модели:

Функция неувязок:

G = = min по а₀, b₁, c₁

Производные по коэффициентам:

где i = 1… n.

приравниваем нулю.

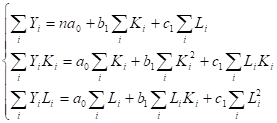
2. Для квадратичной модели:

Функция неувязок:

G = = min по а0, b1, c1, b2, c2.

Производные по коэффициентам:

где i = 1… n.

приравниваем нулю.

(2).

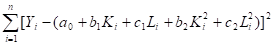
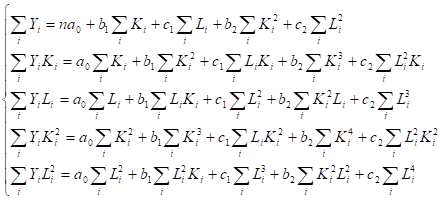
3. Для модели Кобба-Дугласа:

Прологарифмируем функцию:

lnY = lnA + lnK + lnL.

Функция неувязок:

G = = min по A, ,.

Частные производные по коэффициентам:

где i = 1… n.

приравниваем нулю.

(3).

4. Для модели с учетом НТП:

Прологарифмируем функцию:

lnY = lnA + lnK + lnL + 0t.

Функция неувязок:

G = = min по A,, , 0.

Частные производные по коэффициентам:

где i = 1… n.

приравниваем нулю.

(4).

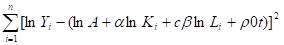
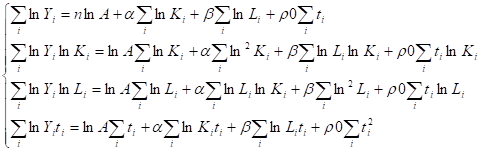
Далее из полученных уравнений находим неизвестные коэффициенты.