Введение. 
Фиктивные переменные

До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.

Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид:

y=a+bx+e,.

где y — количество потребляемого кофе; xцена.

Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: y1=a1+b1x1+e1 и женского пола: y2=a2+b2x2+e2.

Различия в потреблении кофе проявятся в различии средних и. Вместе с тем сила влияния x на x может быть одинаковой, т. е. b"b1"b2. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения y1 и y2 и, вводя фиктивные переменные, можно прийти к следующему выражению:

y=a1z1+a2z2+bx+e,.

где z1и z2 — фиктивные переменные, принимающие значения:

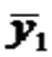
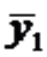
В общем уравнении регрессии зависимая переменная y рассматривается как функция не только цены yx, но и пола (z1,z2). Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда z1=1, то z2=0, и наоборот.

Для лиц мужского пола, когда z1=1 и z2=0, объединенное уравнение регрессии составит:, а для лиц женского пола, когда z1=0 и z2=1:. Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: a1№a2. Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин.

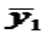
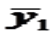
Однако при введении двух фиктивных переменных z1 и z2 в модель y=a1z1+a2z2+bx+e применение МНК для оценивания параметров a1 и a2 приведет к вырожденной матрице исходных данных, а следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т. е. уравнение примет вид.

y=A+a1z1+a2z2+bx+e.

Предполагая при параметре A независимую переменную, равную 1, имеем следующую матрицу исходных данных: .

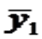
В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям.

y=A+A1z1+bx+e или y=A+A2z2+bx+e,.

т.е. каждое уравнение включает только одну фиктивную переменную z1 или z2.

Предположим, что определено уравнение.

y=A+A1z1+bx+e,.

где z1 принимает значения 1 для мужчин и 0 для женщин.

Теоретические значения размера потребления кофе для мужчин будут получены из уравнения .

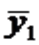
Для женщин соответствующие значения получим из уравнения .

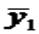
Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: Aдля женщин и A+A1 — для мужчин.

Теперь качественный фактор принимает только два состояния, которым соответствуют значения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.

Мы рассмотрели модели с фиктивными переменными, в которых последние выступают факторами. Может возникнуть необходимость построить модель, в которой дихотомический признак, т. е. признак, который может принимать только два значения, играет роль результата. Подобного вида модели применяются, например, при обработке данных социологических опросов. В качестве зависимой переменной y рассматриваются ответы на вопросы, данные в альтернативной форме: «да» или «нет». Поэтому зависимая переменная имеет два значения: 1, когда имеет место ответ «да», и 0 — во всех остальных случаях. Модель такой зависимой переменной имеет вид:

y=a=b1x1+…+bmxm+e.

Модель является вероятностной линейной моделью. В ней y принимает значения 1 и 0, которым соответствуют вероятности p и 1-p. Поэтому при решении модели находят оценку условной вероятности события y при фиксированных значениях x. Для оценки параметров линейно-вероятностной модели применяются методы Logit-, Probitи Tobit-анализа. Такого рода модели используют при работе с неколичественными переменными. Как правило, это модели выбора из заданного набора альтернатив. Зависимая переменная y представлена дискретными значениями (набор альтернатив), объясняющие переменные xi — характеристики альтернатив (время, цена), zj — характеристики индивидов (возраст, доход, уровень образования). Модель такого рода позволяет предсказать долю индивидов в генеральной совокупности, которые выбирают данную альтернативу.

Среди моделей с фиктивными переменными наибольшими прогностическими возможностями обладают модели, в которых зависимая переменная y рассматривается как функция ряда экономических факторов xi и фиктивных переменных zj. Последние обычно отражают различия в формировании результативного признака по отдельным группам единиц совокупности, т. е. в результате неоднородной структуры пространственного или временного характера.