Разработка курса по выбору «Паркеты» для старшеклассников

Многогранники в 1700—2000 годах В данный период главным стимулом интереса к многогранникам стало не искусство, а математика. Так Леонардом Эйлером (1707−1783) была открыта его знаменитая формула Г +В = Р + 2 (сумма числа граней и вершин равна числу ребер, увеличенному на 2), Шарль Каталан исследовал многогранники, двойственные архимедовым телам. В 1812 году Ронделе опубликовал развертки… Читать ещё >
Разработка курса по выбору «Паркеты» для старшеклассников (реферат, курсовая, диплом, контрольная)
Пояснительная записка курса по выбору Актуальность программы обоснована необходимостью расширения знаний обучающихся по предмету «Математика», развитием общего кругозора школьников, так как в курс входят занятия по истории математики. Данный курс по выбору, представленный в предлагаемой работе, рассчитан на старших школьников. Вместе с тем, часть собранного учебного материала с успехом можно предложить и учащимся 9 класса на курсе по выбору в условиях предпрофильной подготовки. Задача курса по выбору — развитие интереса к математике и ее истории, развитие навыков творческой и исследовательской работы. Отбор содержания курса проводился с учетом возрастных особенностей обучающихся и с учетом разнообразия форм деятельности школьников.
Занятие 1. История возникновения и развития темы «Паркеты».
С древних времен паркеты были незаменимой частью жизни человека. Так паркет встречался в архитектуре (например, примитивное замощение пола деревянными дощечками), живописи. Примером последнего может служить картина «Рыбы и лягушки» Мариуса Эшера (рис. 1).

Рис. 1.
Само слово «паркет» пришло к нам из Франции. В средние века во Франции им обозначали небольшой парк, немного спустя — предназначенную для аудиенций часть зала, покрытую ковром. Ковры постепенно исчезли, а название закрепилось за настилами из деревянных планок и распространилось за пределами Франции.
В России выкладывать паркет впервые начали в начале XVIII века. Это было нововведением Петра I, который привез целый цех краснодеревщиков с Запада, в частности, из Германии. Он делался из дубовых клепок и ложился в рисунок, который в народе прозвали «елочка», а сам он носил называние «косящатый» (рис. 2).
Примеры наиболее распространенных современных паркетов представлены на рисунке 3: а) двойная плетенка; б) шереметьевка;
- в) наборный.
- а)

- б)
- в)


Рис. 3.
Занятие 2. Паркеты: основные понятия Что такое паркет?
В различных источниках встречаются немного отличающиеся друг от друга определения, однако чаще всего дается следующее:
Паркетом из многоугольников будем называть замощение плоскости многоугольниками, при котором вся плоскость оказывается покрытой ими, и любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо вообще не имеют общих точек.
Разновидности.
Правильным называют паркет, если он составлен из равных правильных многоугольников и вокруг каждой вершины правильные многоугольники расположены одним и тем же способом. На рисунке 4 представлены правильные паркеты из:
- а) квадрата; б) правильного треугольника; в) правильного шестиугольника.
- а)

- б)
- в)
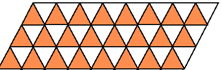

Рис. 4.
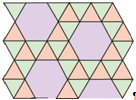
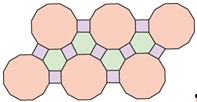
Полуправильным называют паркет, если он состоит из правильных многоугольников (возможно с разным числом сторон), одинаково расположенных вокруг каждой вершины (рис. 5).



Теперь представим названные паркеты подробнее. Начнем с правильных паркетов. Почему только эти три фигуры могут составлять правильный паркет? Докажем, что другими равными правильными многоугольниками заполнить плоскость нельзя. Известно, что углы правильного n-угольника равны 180о (n-2)/n. Если в одной вершине паркета сходится m правильных n-угольников, то должно выполняться равенство m*180o (n-2)/n=360o, откуда с помощью преобразований получаем m=2n/(n-2). Давайте попробуем решить полученное уравнение для n=2, n=3, n=4, n=5, n=6. Получим, что возможными допустимыми значениями для n при решении данного уравнения в целых числах являются 3, 4, 6.
Упражнения Можно ли составить паркет из правильных пятиугольников, семиугольников?
Решение. Нельзя, так как при решении уравнения m=2n/(n-2) для n=5 и для n=7 получаем дробные значения m, что противоречит условию о целых значениях переменной.
Существует ли такой пятиугольник, из которого можно составить паркет, заполняющий плоскость?
Решение. Несколько примеров решения приведены на рисунке 6.
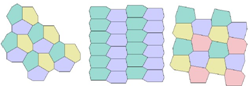
Рис. 6.
Придумайте паркет, составленный из равных фигур.
Решение. Решением этой задачи может служить большое число различных паркетов. В качестве примера решения можно взять паркеты, изображенные на рисунке 7.

Рис. 7.
Домашнее задание Творческая задача. Придумайте паркет, составленный из равных фигур, ограниченных кривыми линиями.
Решение. Пример решения задачи на рисунке 8.

Рис. 8.
Занятие 3. Полуправильные паркеты Полуправильным называют паркет, если он состоит из правильных многоугольников (возможно, с разным числом сторон), одинаково расположенных вокруг каждой вершины.
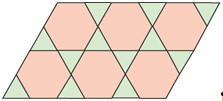
Рассмотрим, какие можно составить паркеты, удовлетворяющие этому условию. Для этого рассмотрим суммы углов различных правильных многоугольников, расположенных вокруг одной точки. Например, мы можем расположить вокруг одной точки 2 квадрата и 3 правильных треугольника, как показано на рисунке 9, так как сумма углов будет равняться 360о (90о+90о+60о+60о+60о=360о).

Рис. 9.
Продолжая рассматривать различные суммы углов, получим, что еще в одной вершине могут сходиться 4 правильных треугольника и правильный шестиугольник, как на рисунке 10.
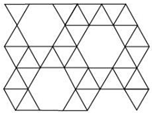
Рис. 10.
На рисунке 11 представлен паркет, в котором вокруг одной точки расположены 2 правильных шестиугольников и 2 правильных треугольников.

Рис. 11.
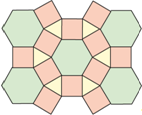
Так же можно построить паркет, состоящий из квадратов и правильных восьмиугольников (рис. 12).
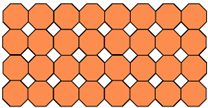
Рис. 12.
На рисунке 13 показан паркет из правильных треугольников и двенадцатиугольников (рис. 13).

Рис. 13.
Если рассмотреть составление паркета из трех различных видов фигур, то получим, что можно составить паркет из правильного треугольника, двух квадратов и правильного шестиугольника (рис. 14).
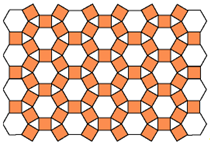
Рис. 14.
На рисунке 15 представлен паркет, составленный из правильных шестиугольника и двенадцатиугольника и квадрата.
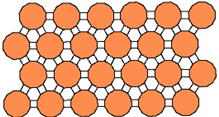
Рис. 15.
Итак. Получили, что полуправильных паркетов всего восемь. Докажем это. Обозначим через б1, б 2, … углы правильных многоугольников, имеющих общую вершину. Расположим их в порядке возрастания б 1? б 2? …. Составим таблицу, содержащую возможные наборы углов, и укажем соответствующие паркеты.
Рассмотрим таблицу 1, содержащую все возможные наборы углов.
Таблица 1.
б 1. | б 2. | б 3. | б 4. | б 5. | б 6. | б 1+ б 2+…=360о. | |
60о. | 60о. | 60о. | 60о. | 60о. | 60о. | Правильный паркет из 3-ов (рис. 4, б). | |
60о. | 60о. | 60о. | 60о. | 120о. | Паркет из 3-ов и 6-ов (рис. 10). | ||
60о. | 60о. | 60о. | Два паркета из 3-ов и 4-ов (рис. 9). | ||||
60о. | 60о. | 150о. | Нет паркета. | ||||
60о. | 60о. | 120о. | 120о. | Паркет из 3-ов и 6-ов (рис. 11). | |||
60о. | 120о. | Паркет из 3-ов, 4-ов, 6-ов (рис. 14). | |||||
60о. | 150о. | 150о. | Паркет из 3-ов и 12-ов (рис. 13). | ||||
Правильный паркет из квадратов (рис. 4, а). | |||||||
120о. | 150о. | Паркет из 4-ов, 6-ов, 12-ов (рис. 15). | |||||
135о. | 135о. | Паркет из 4-ов и 8-ов (рис. 12). | |||||
120о. | 120о. | 120о. | Правильный паркет из 6-ов (рис. 4, в). | ||||
Таким образом, мы получили 11 паркетов, из которых три правильных и 8 полуправильных.
Упражнения Задача. Докажите, что для любого четырехугольника существует паркет, состоящий из четырёхугольников, равных данному.
Решение. Пусть дан четырёхугольник АВСD (рис. 16). Рассмотрим центрально-симметричный ему четырёхугольник относительно середины стороны АВ. Исходный четырёхугольник АВСD обозначим цифрой 1, а симметричный — цифрой 2. Теперь четырёхугольник 2 отразим симметрично относительно середины его стороны ВС. Полученный четырёхугольник обозначим цифрой 3 и отразим его симметрично относительно середины его стороны CD. Полученный четырёхугольник обозначим цифрой 4. Четырёхугольники 1, 2, 3 и 4 примыкают к общей вершине, А углами А, В, С и D. Поскольку сумма углов четырехугольника равна 360 ??, то эти четырёхугольники заполнят часть плоскости вокруг общей вершины. Такое же построение можно провести вокруг каждой новой вершины, что и даст искомое заполнение плоскости.
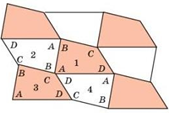
Рис. 16.
Самостоятельная работа. Постройте паркет из невыпуклого четырехугольника.
Домашнее задание Задача 1. Можно ли составить паркет из равных треугольников произвольной формы?
Решение. Да (рис. 17).
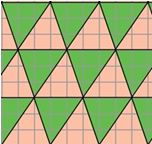
Рис. 17.
Занятие 4. Задачи на разрезание Тема «Паркеты» тесно связана с задачами на разрезания. Часто приемы построения паркета помогают в решении таких задач, и наоборот. На этом уроке мы рассмотрим некоторые задачи на разрезание.
Задача 1. Разрежьте параллелограмм на две части, из которых можно сложить прямоугольник (рис. 18).

Рис. 18.
Решение показано на рисунке 19.
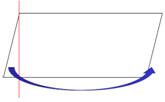
Рис. 19.
Задача 2. Разрежьте треугольник (рис. 20) на три части, из которых можно сложить прямоугольник.
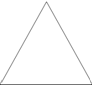
Рис. 20.
Решение представлено на рисунке 21 (для решения проводим среднюю линию треугольника).

Рис. 21.
Задача 3. Разрежьте трапецию (рис. 22) на две части, из которых можно сложить треугольник.

Рис. 22 Решение показано на рисунке 23.
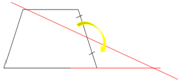
Рис. 23.
Задача 4. Разрежьте фигуру (рис. 24), составленную из трех равных квадратов, на четыре равные части.
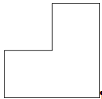
Рис. 24.
Решение представлено на рисунке 25.
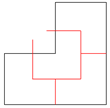
Рис. 25.
Задача 5. Прямоугольник со сторонами 4 и 9 (рис. 26) разрежьте на две равные части, из которых можно сложить квадрат.

Рис 26.
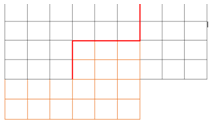
Рис. 27.
Занятие 5. Задачи на краски Задача 1. Какое наименьшее число красок потребуется для раскраски паркетов на рисунке 28 так, чтобы соседние многоугольники были окрашены в разные цвета (такая раскраска называется правильной)?
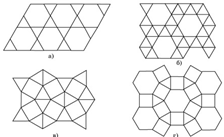
Рис. 28.
Решение. а) 2; б) 3; в) 3; г) 2 (рис. 29).
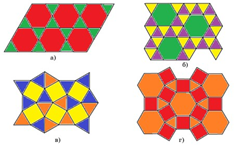
Рис. 29.
Задача 2. Составьте паркет из греческих крестов (рис. 30).
Раскрасьте получившийся паркет двумя красками.

Рис. 30 Решение указано на рисунке 31.

Рис. 31.
Занятие 6. Многогранники Многогранники — один из немногих видов геометрических фигур, которые окружают нас. В разные времена в разных странах многогранники привлекали внимание не только математиков, но и архитекторов, биологов, скульпторов. Эти фигуры завораживают по сей день своей красотой своих форм и порой их сложностью. История многогранников начинается в далекие времена. Многогранники бывают выпуклые и невыпуклые (рис. 32).

Рис. 32.
Выпуклым называется многогранник, который является выпуклой фигурой, т. е. вместе с любыми двумя своими точками целиком содержит соединяющий их отрезок.
Среди многогранников особенно выделяются правильные многогранники. Правильный многогранник — это выпуклый многогранник, у которого все грани являются равными правильными многоугольниками, и в каждой вершине сходится одинаковое число ребер.
Существует только 5 типов правильных многогранников (рис. 33).
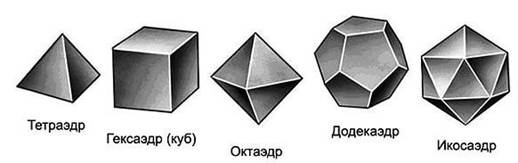
Рис. 33.
Существует еще один привлекательный и содержательный тип многогранников, это дельтоэдры. Дельтоэдр — это выпуклый многогранник, гранями которого являются равные между собой равносторонние треугольники (рис. 34).
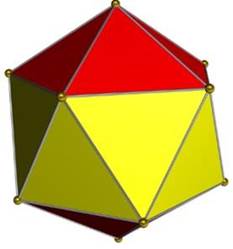
Рис. 34.
Среди них есть правильные многогранники, такие, как тетраэдр, октаэдр, икосаэдр (рис. 34).
Остановимся еще на звездчатых многогранниках. Звездчатыми многогранниками занимались многие ученые математики. Первым их изучил Томас Брадвардин (1290−1349). Чуть позже ими занимался Иоганн Кеплер (1571−1630), который попытался описать эти многогранники. Он использовал два способа построения правильных звездчатых многогранников: путем продолжения ребер и граней правильных исходных многогранников. Так им была получена первая пара звездчатых многогранников: малый звездчатый додекаэдр и большой додекаэдр. Еще через несколько лет была открыта вторая пара таких многогранников французским математиком и физиком Луи Пуансо (1777−1859): большой звездчатый додекаэдр и большой икосаэдр. Постепенно открытие различных форм звездчатых многогранников привело к тому, что на данный момент насчитывают 59 звездчатых форм икосаэдра. Некоторые из них показаны на рисунке 35.

Рис. 35.
Домашнее задание Изготовьте модель многогранника (по усмотрению учителя).
Найдите пример невыпуклого многогранника, у которого все грани являются выпуклыми многоугольниками.
Ответ. Примером такого многогранника может служить пространственный крест (рис. 36).
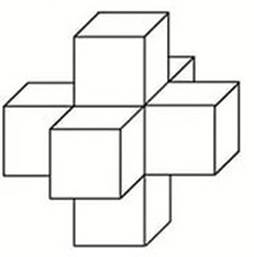
Рис. 36.
Существуют ли отличные от куба многогранники, все грани которых являются равными между собой квадратами?
Ответ. Да, существуют. Например, многогранник, изображенный на рисунке 36.
Занятие 7. История многогранников (к данному уроку была представлена презентация, данная в приложениях) Доисторический период Благодаря археологическим раскопкам, мы можем судить о том, насколько велика история многогранников. Возраст находок (множество сфер, высеченных из камня), сделанных учеными в Шотландии оцениваются в 4 тысячи лет. Ювелирные украшения в форме многогранников, возраст которых насчитывает несколько тысяч лет, были найдены в Африке, Египте. Некоторые источники утверждают, что тетраэдр, октаэдр и куб были известны еще в Древнем Вавилоне (3000 лет до н. э.). Издавна многогранники использовались при изготовлении игральных костей. Самой старинной игральной костью считается кость в форме додекаэдра, датируемая 1000 годом до н. э.



Рис. 37.
Многогранники в Древней Греции и Древнем Риме Пифагор Самосский (582−507 гг. до н. э.) создал космологическое учение, связавшие правильные многогранники с устройством Вселенной. По его философии родился мистицизм, связанный с соотнесением многогранников с четырьмя основными элементами природы: тетраэдр — огонь, куб — земля, октаэдр — воздух, икосаэдр — вода, а додекаэдр отождествляли с небесной сферой.
Первая теория о пяти правильных телах принадлежит великому греческому математику Теэтету Афинскому (415−369 гг. до н. э.). Однако правильные многогранники обрели популярность благодаря Платону. Именно поэтому правильные многогранники в науке часто называют.
«Платоновы тела».
Следующим важным событием в истории многогранников было появление Великого труда Евклида.
Его «Начала» представляют собой собрание из тринадцати книг, в котором представлены все существующие на тот момент знания о геометрии. Каждая из книг начинается с общих утверждений, или аксиом. Затем следуют 15 постулатов геометрии, задающих правила игры, и на их основе последовательно доказываются в общей сложности 465 предложений или теорем. Так в книге XI описаны факты, касающиеся размеров многогранников, книга XII посвящена объемам призм и пирамид, книга XIII — правильным многогранникам. Благодаря Евклиду интерес греческих математиков к правильным многогранникам заметно возрос.
Эпоха Возрождения В это время изучением многогранников так или иначе занимались живописцы и архитекторы. Перед ними стоял вопрос: «Как изобразить трехмерное пространство?» Создателем новой теории перспективы считается архитектор и художник Филиппо Брунеллески (1377−1446), однако картины с перспективой можно увидеть и у других мастеров, живших раннее.
Способы изображения многогранников, кубооктаэдров и звездчатых многогранников изучал Лука Пачоли (1445−1517). Свои рассуждения и результаты он описал в книге «О божественной пропорции», иллюстрации к которой выполнил его друг — Великий Леонардо да Винчи (1452−1519). Одна из иллюстраций представлена на рисунке 38.
В 1567 году была опубликована книга Лоренца Стоера Geometria et Perspectiva, в которой он применил методы перспективы при изображении многогранников.
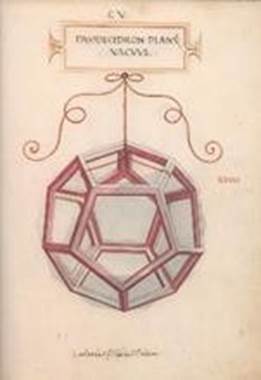
Рис. 38.
Многогранники в 1700—2000 годах В данный период главным стимулом интереса к многогранникам стало не искусство, а математика. Так Леонардом Эйлером (1707−1783) была открыта его знаменитая формула Г +В = Р + 2 (сумма числа граней и вершин равна числу ребер, увеличенному на 2), Шарль Каталан исследовал многогранники, двойственные архимедовым телам. В 1812 году Ронделе опубликовал развертки правильных многогранников на плоскости. Чуть позднее Макс Брюкнер создал коллекцию из 146 бумажных многогранников. В 1900 году Давид Гильберт в своем знаменитом выступлении в Париже в числе 23 математических проблем упомянул задачи о многогранниках. Он поставил такую задачу: можно ли разрезать многогранники равного объема на конечное число равных частеймногогранников? Несколькими годами после Макс Ден доказал, что нельзя. Полный и окончательный список 92 неоднородных многогранников с правильными гранями составил в 1966 году Норман Джонсон. Благодаря этим и многим другим открытиям, связанным с многогранниками, интерес к ним сохранялся на протяжении всего столетия.
Многогранники в наши дни На протяжении многих лет и по сей день многогранники включены в школьный курс геометрии и изобразительного искусства. Так же по сей день не прекращается изучение многогранников. В этом значительно помогают компьютерные технологии, в частности, компьютерная графика. Существует много различных программ, позволяющих не только изобретать многогранники (Рис. 39), но и перемещать, крутить и проводить много других манипуляций с ними, что сильно облегчает процесс обучения геометрии.

Рис. 39.
Домашнее задание Индивидуальные задания. Сообщение на следующие темы.
Пифагор Самосский. Биография и главные открытия.
Иоганн Кеплер. Биография и главные открытия.
Леонард Эйлер. Биография и главные открытия.
Давид Гильберт. Биография. Проблемы Гильберта.
Леонардо да Винчи. Биография и работы.
Великий труд Евклида.
Платоновы тела.
Занятие 8. Задачи с многогранниками Аналогично тому, как плоскость можно покрыть многоугольниками, так и пространство можно заполнить некоторыми многогранниками. Чтобы узнать, какими именно, рассмотрим следующую задачу.
Задача. Какими равными одноименными правильными многогранниками можно заполнить пространство?
Мы ответим на этот вопрос с помощью эксперимента. Возьмем набор моделей одинакового размера правильных многогранников и, прикладывая их одну к другой, увидим, какие их них вплотную прилегают друг к другу, а какие нет.
Если решать задачу теоретически, получим такое решение. Пусть б — внутренний угол правильного многоугольника (грани правильного многогранника), число правильных многоугольников, сходящихся в одной вершине, n. Ясно, что равенство n*б=360o может выполняться только для одного правильного многогранника — куба, у которого б=90о.
Вывод. Из правильных многогранников только кубами можно заполнить все пространство.
Рассмотрим теперь неправильные многогранники. Из представленного заполнения кубами можно получить новое заполнение пространства равными двенадцатигранниками, у которых все грани — равные ромбы. Такой двенадцатигранник называется ромбододекаэдром.
Для построения ромбододекаэдра берут кубы двух цветов и располагают их в пространстве в шахматном порядке (пространственный аналог плоской бесконечной шахматной доски). Затем кубы одного цвета убирают. Образовавшуюся пустоту заполняют шестью равными пирамидами с общей вершиной в центре выброшенного куба. После присоединения к оставшемуся кубу другого цвета всех прилегающих пирамид, у которых основаниями являются грани выброшенного куба, получим ромбододекаэдр. Полученное заполнение представлено на рисунке 40.
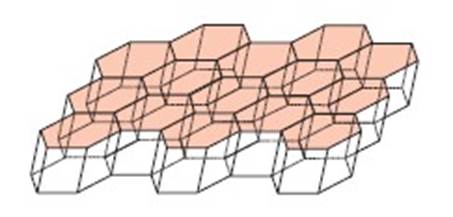
Рис. 40.
Также пространство можно заполнить и равными полуправильными многогранниками — усеченными октаэдрами (ис. 41).

Рис. 41.
Упражнение Найдите самый короткий путь по поверхности куба A… D1 из вершины A в вершину C1.
Ответ. Путь, состоящий из двух отрезков, соединяющих данные точки с серединой ребра BB1.
Может ли в пирамиде быть 21 ребро?
Ответ. Нет. В пирамиде четное число ребер.
Докажите, что у любого многогранника число граней с нечетным числом ребер четно.
Решение. Предположим, что число граней с нечетным числом сторон нечетно. Тогда общее число сторон в этих гранях будет нечетным. Общее число сторон в гранях с четным числом сторон четно. Поэтому общее число сторон всех граней будет нечетно. Однако каждая сторона граней входит ровно в две грани, и при подсчете общего числа сторон, входящих в грани, мы считаем каждую сторону дважды. Таким образом, число сторон в гранях многогранника равно удвоенному числу его ребер, т. е является четным числом. Получили противоречие. Значит, число граней с нечетным числом сторон должно быть четным.