Технология агроклиматического районирования почв предгорных агроландшафтов при закладке садов в Кабардино-Балкарии

ТЕХНОЛОГИЯ АГРОКЛИМАТИЧЕСКОГО РАЙОНИРОВАНИЯ ПОЧВ ПРЕДГОРНЫХ АГРОЛАНДШАФТОВ ПРИ ЗАКЛАДКЕ САДОВ В КАБАРДИНО-БАЛКАРИИ

Интенсивное развитие садоводства в Северо-Кавказском федеральном округе и в частности в Кабардино-Балкарии требует освоения предгорной зоны, а значит выбора территорий наиболее пригодных для садоводства. Критериями для принятия решений наряду с агроэкологическими особенностями, являются также метеорологические условия, существенно влияющие на урожайность.

Методология проведения работ. Для эффективного решения такого рода задач и принятия решений, необходимо иметь методы количественного прогноза влияния местоположения склона, его крутизны, а также характеристик мелиоративных приемов на микроклимат почвы.

В предлагаемой статье рассматривается модель тепломассопереноса в почве, позволяющая прогнозировать изменения теплового и водного режимов почвы под влиянием указанных факторов.

Основная часть

Материал содержащийся в опубликованных работах посвященных изучению различных аспектов теплои массообмена [1, 2, 3, 4, 5, 6, 7, 9, 10] позволяет наметить основные концептуальные подходы к построению такого рода модели.

В условиях пересеченного рельефа местности, поля температуры и влажности почвы трехмерны, особенно возле вершин и оснований склонов. Для нахождения температурного поля в почве требуется иметь двухили трехмерные решения уравнения теплопроводности. Отыскание таких решений связано с большими математическими трудностями. В отдельных случаях, как свидетельствует экспериментальный материал, возможна одномерная постановка задачи тепловлагопереноса, если участок склона ровный и достаточно удален от области с явно выраженной неоднородностью тепломассопереноса, то поля температуры и влажности почвы, одномерны. Целесообразность одномерной постановки задачи связана с необходимостью создания простого алгоритма для прикладных целей.

С учетом изложенных соображений математическая модель теплопереноса в почве на склоне строится по тому же алгоритму, что и для ровной поверхности [6] краевая задача формулируется следующим образом:

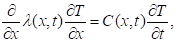
(1).

где:

л — тепловодность почвы;

Т — температура почвы;

С — объемная теплоемкость; t — время;

x — пространственная координата направленная перпендикулярно поверхности;

h — нижняя граница почвенного массива.

Краевые условия к уравнению теплопроводности записываются в виде:

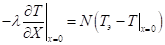
• (2)
• (3)

где:

T_э — эквивалентная температура окружающей среды;

N — эффективный коэффициент теплообмена;

F (t) — функция описывающая временные изменения температуры на глубине h;

F₀(х) — начальное распределение температур.

Сформулированная краевая задача применима без изменений только для тех случаев, когда почвенный массив однороден, либо состоит из слоев параллельных поверхности склона.

В горных условиях эти случаи встречаются нечасто, наиболее характерным является произвольное расположение слоев, при этом функции (x, t) и C (x, t) будут двухили трехмерны, и применение одномерной модели становится невозможным.

Рассмотрим способ преодоления такого рода затруднений, для этого выделим в пределах расчетного участка области с характерным распределением теплофизических свойств. Обозначим площадь каждой такой области через F_i. Опишем эти распределения слоистыми структурами параллельными поверхности склона:

урожайность мелиоративный почва микроклимат.

Воспользуемся известными зависимостями теории теплопереноса, преобразуем толщину каждогого слоя iтой области h _iм с коэффициентами теплопереноса _iм, C_iм, м=1,2,3,…m таким образом, чтобы их термические сопротивления оставались неизменными.

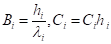
(4).

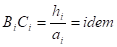
(5).

где:

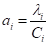
Преобразованную (эквивалентную) толщину слоя Можно определить по формуле:

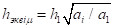
.(6).

Эквивалентное значение расчетной глубины в пределах области i равно.

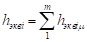
(7).

Эквивалентное значение расчетной глубины в пределах области i.

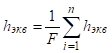
(8).

Эквивалентное значение расчетной глубины для всего участка склона находится по формуле.

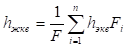
(9).

где: F — площадь расчетного участка.

Таким образом почвенный массив толщиной h и состоящий из m области с различными теплофизическими свойствами преобразован в однородный многослойный объект толщиной h_экв с коэффициентами переноса _1 м, С_1 м. Термические сопротивления исходного и преобразованного объектов равны, а значит и усредненные по площади температуры должны быть близки друг другу, область i =1, при h= h_экв можно трактовать как информативную, а величины ₁, С₁, h_экв как входные параметры при расчетах по одномерной модели.

Алгоритм теоретического описания влажностного режима почвы на склоне, также можно построить в одномерной постановке, однако с ограничением однородности структуры почвенного массива вдоль поверхности склона, необходимо учитывать особенность гравитационной составляющей. В одномерной постановке уравнение влагопереноса для равнинных условий формулируется в виде.

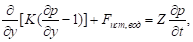
(10).

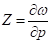
(11).

где: у — пространственная координата, направленная строго по вертикали вглубь почвы;

K — коэффициент влагопроводности;

Р — капиллярный потенциал;

F_{ист.вод} — функция источника;

щ — влажность почвы.

Краевые условия к этому уравнению формулируются:

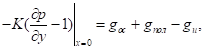
(12).

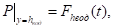
• (13)
• (14)

где: g_ос — интенсивность осадков;

g_пол — интенсивность расхода воды на полив;

F_hвод(t) — функция описывающая временные изменения Р на глубине h_вод;

F_начвод(y) — начальное распределение капиллярного потенциала Для случая расположения поверхности склона под некоторым углом к горизонту б, влияние гравитационной составляющей можно учесть из соотношения между координатами:

Х = ycosб (15).

где: б — угол наклона поверхности склона к горизонту.

Подставим это соотношение в 10−14 и после преобразований получим.

Подставляя это соотношение в уравнение влагопереноса и краевые условия к нему, получим:

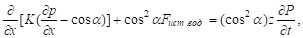
(16).

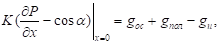
(17).

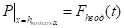
(18).

. (19).

Нижние границы моделируемой области почвенного массива при раздельном решении задач теплои влагопереноса могут не совпадать h?.

Идентификация параметров входящих в формулы (1)-(3) и (16)-(19) и учитывающих взаимодействие между метеорологическим режимом, растительным покровом и почвой на склоне осуществляется по методике, аналогичной горизонтальной поверхностями [4, 8]. Алгоритм расчета остается без изменений, изменения вносятся лишь в отдельные операции, в частности поток прямой солнечной радиации, поступающий на поверхность склона можно оценить из соотношения соответственно азимуты солнца и проекции нормали к склону на горизонтальную плоскость, отсчитываемы от плоскости меридиана по часовой стрелке; б — угол наклона склона; индексами обозначены С, Г и — соответственно склон, горизонтальная и перпендикулярная поверхности.

(20).

(21).

Решая совместно (20) и (21), можно получить:

(22).

где:

б и — являются характеристиками склона;

h₀ и Ш₀ — входными климатологическими параметрами.

Поток рассеянной изотропной атмосферной радиации приходящийся на поверхность склона, согласно [7, 9]:

(23).

(24).

где:

С — константа.

Из совместного решения (23) и (24), получаем.

(25).

Соотношения (22) и (25), дают для потока суммарной радиации.

(26).

Величины S_Г и D_Г являются входными параметрами, информация о них содержится в гидрометфондах.

Для случая расчета средних суточных значений теплового и водного режимов почвы используют средние суточные метеопараметры.

Средняя суточная сумма солнечной радиации: как известно равна:

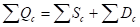
(27).

В работе [9] предложена формула для приближенного расчета суточных сумм радиации для склонов крутизной б не более 30 градусов для условий безоблачного неба в летний период.

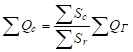
(28).

Формулу (28), можно записать в форме наиболее удобной с точки зрения информационного обеспечения:

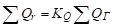
(29).

Значения находятся по данным [9], в зависимости от широты местности и угла наклона склона б. Переход от сумм к потокам Можно осуществить по формуле.

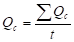
(30).

где: t — продолжительность интервала осреднения.

Лучистый теплообмен в инфракрасной области спектра по данным [7, 9].

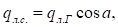
(31).

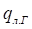
где: — поток теплового излучения горизонтальной поверхности.

Идентификация конвективных и эвапотранспирационных потоков тепла связана со значительными трудностями. В условиях пересеченного рельефа местности, неоднородного растительного покрова, направленных воздушных течений и интенсивной турбулентности приводит к искажению локальных значений метеорологических величин в приземном слое воздуха [6, 7].

В настоящее время отсутствуют надежные алгоритмы, и теоретическое описание расчета конвективного переноса тепла и влаги в приземном слое воздуха. Поэтому определения параметров, позволяющих идентифицировать эти потоки, возможно лишь для отдельных частых случаев, характерным для горизонтальных поверхностей, достойного удаленных от вершин и оснований склонов. Тогда для определения параметров позволяющих идентифицировать эти потоки можно использовать расчетные схемы изложенные в [4, 8].

Экспериментальная база. Обеспечение расчетов составляющих уравнения теплового баланса деятельной поверхности входной метеоинформацией, связано с некоторыми трудностями, т.к. метеостанции обычно располагаются на равнинных территориях. Используя эмпирические зависимости, связывающие значения метеопараметров на склоне с их значениями на ровных участках, можно преодолеть эти затруднения, обоснование и количественный анализ которых дается в работах [5, 6, 7]. Эти соотношения имеют приближенный характер, тем не менее их можно использовать для формирования исходных данных.

Значение i-го метеопараметра на склоне можно определить по формуле.

.

где: — значение i-го метеопараметра на ровной поверхности;

— эмпирические коэффициенты.

Для идентификации коэффициентов используются данные [6] где содержатся сведения о разностях температур на склоне и ровным участком.

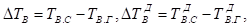
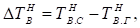
где:

— температура воздуха; индексами Д и Н обозначены день и ночь.

Используя эти разности можно полагать, что .

Влияние пересеченного рельефа местности на скорость ветра можно учесть по данным [5, 6, 7], из которых следует, что В_u.1 изменяется в диапазоне от 1,5 до 0,6, а В_u.o=0.

Пересеченный рельеф местности оказывает воздействие на формирование облачности и влажности воздуха в нижней части приземного слоя [5,6,7]. Ввиду отсутствия количественной информации об этом влиянии, в первом приближении можно принять для облачности, а влажности воздуха, … .

Характеристики склона, ориентация и крутизна влияют на перераспределение осадков. По данным работы [6, 7], можно идентифицировать коэффициенты варьирует в зависимости от зоны увлажнения при северной ориентации от 0,84 до 1, а при южной — от 0,92 до 1.

Результаты исследования Для численного решения сформулированной тепловлагообменной задачи разработан алгоритм и написана программа, за основу приняты алгоритм и программа созданные в работе [8].

Программа ориентирована на использование стандартной метеоинформации и предусматривает расчет среднесуточных значений составляющих уравнений теплового и водного балансов поверхности почвы, а также параметров входящих в граничное условие. В программе реализована возможность автоматизированного сравнения вариантов расчета и определения разностей.

где индексами i и j обозначены сравниваемые варианты.

Область применения: районирование территории предгорных агроландшафтов.

Выводы

Разработанная модель и реализующая её программа формирования теплового режима почвы позволяет прогнозировать термические эффекты в почве в зависимости от ориентации склона его крутизны, мелиоративных приемов.

• 1. Архипова Е. П., Глебова М. Я., Романова Е. Н. Особенности микроклимата пахотных склонов. Труды 220, 1960. Вып. 91. С. 3−15.
• 2. Берсиров Т. Г. Эффективность применения пленочной мульчи в условиях склонов предгорной зоны Кабардино-Балкарии // Сб. трудов по агрономической физике. Л.: Гидрометеоиздат, 1973. Вып. 31. С. 160−163.
• 3. Берсиров Т. Г. Изучение термической эффективности террасирования склонов в предгорной зоне Кабардино-Балкарии // Сб. трудов по агрономической физике. Л.: Гидрометеоиздат, 1973. Вып. 31. С. 157−159.
• 4. Куртенер Д. А., Усков И. Б. Климатические факторы и тепловой режим в открытом и защищенном грунте. Л.: Гидрометеоиздат, 1982. 231 с.
• 5. Романова Е. Н., Мосолова Г. И., Береснева И. А. Микроклиматология и ее значение для сельского хозяйства. Л.: Гидрометеоиздат, 1983. 245 с.
• 6. Романова Е. Н. Микроклиматическая изменчивость основных элементов климата. Л.: Гидрометеоиздат, 1977. 279 с.
• 7. Роджер Г. Барри. Погода и климат в горах. Л.: Гидрометеоиздат, 1984. 310 с.
• 1. Arkhipova E.P., Glebova M.Ya., Romanova E.N. Osobennosti mikroklimata pakhotnykh sklonov. Trudy 220, 1960. Vyp 91. S. 3−15.
• 2. Bersirov T.G. Effektivnost primeneniya plenochnoj mulchi v usloviyakh sklonov predgornoj zony Kabardino-Balkarii // Sb. trudov po agronomicheskoj fizike. L.: Gidrometeoizdat, 1973. Vyp. 31. S.160−163.
• 3. Bersirov T.G. Izuchenie termicheskoj effektivnosti terrasirovaniya sklonov v predgornoj zone Kabardino-Balkarii // Sb. trudov po agronomicheskoj fizike. L.: Gidrometeoizdat, 1973. Vyp. 31. S.157−159.
• 4. Kurtener D.A., Uskov I.B. Klimaticheskie faktory i teplovoj rezhim v otkrytom i zaschischennom grunte. L.: Gidrometeoizdat, 1982. 231 s.
• 5. Romanova E.N., Mosolova G.I., Beresneva I.A. Mikroklimatologiya i ee znachenie dlya selskogo khozyajstva. L.: Gidrometeoizdat, 1983. 245 s.
• 6. Romanova E.N. Mikroklimaticheskaya izmenchivost osnovnykh elementov klimata. L.: Gidrometeoizdat, 1977. 279 s.
• 7. Rodzher G. Barri. Pogoda i klimat v gorakh. L.: Gidrometeoizdat. 1984. 310 s.