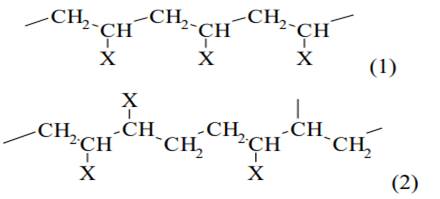По регулярности строения цепи

Регулярные Нерегулярные Если в цепи полимера наблюдается монотонное чередование звеньев, то есть соблюдается дальний порядок звеньев по цепи, то полимер называют регулярным. Если нарушается монотонное чередование звенев в цепи, то полимер нерегулярен.

Нерегулярность цепи обуславливается разными причинами. Одна из таких причин это различный способ присоединения друг к другу мономерных звеньев. При реакции полимеризации звенья могут присоединяться по схеме (1) или по схеме (2).

По первой схеме присоединение называется «голова к хвосту», по второй — «голова к голове». 17 При полимеризации мономеры большей частью присоединяются по типу «гoлoвa к xвоcтy», однако отдельные мономеры в некоторых участках цепи могут соединятся по второму типу, что нарушает регулярность цепи. Нерегулярность цепи может обуславливаться так же разной степенью разветвленности, так как места присоединения боковой цепи, число ответвлений и их длина могут быт различны.

Так же нерегулярность цепи может быть следствием беспорядочного чередования мономеров различного химического состава. Этот вид нерегулярности в большинстве случаев у сополимеров, так как при совместной полимеризации остатки мономеров могут соединяться хаотически.

По развитию деформации при комнатных температурах

Полимеры делятся на пластомеры и эластомеры. Полимеры, которые легко деформируются при комнатной температуре, называют эластомерами, трудно деформируемые — пластомерами (пластиками).

По полярности

Полимеры делят на полярные и неполярные. Степень полярности оценивают величиной дипольного момента (мо), равной произведению заряда на расстояние между зарядами (Кл · м). Дипольный момент макромолекулы равен векторной сумме дипольных моментов полярных групп, распределенных вдоль цепи. Если полярные группы в цепях расположены симметрично, то их электрические поля взаимно компенсируются и дипольные моменты таких полимеров равны нулю (политетрафторэтилен, полиизобутилен).