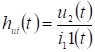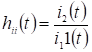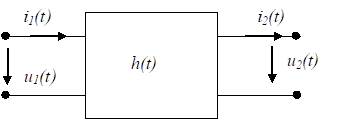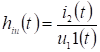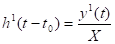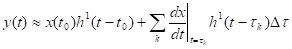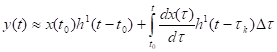Переходные процессы в линейных электрических цепях

Переходные характеристики ЛЭЦ с сосредоточенными элементами

Отношение реакции электрической цепи на ступенчатое воздействие к величине воздействия при нулевых начальных условиях называют переходной характеристикой цепи.

Переходные характеристики электрических цепей относятся к числу нормированных временных характеристик устойчивых линейных электрических цепей. При этом с неограниченным ростом времени значения переходной характеристики асимптотически приближаются к некоторой конечной величине, характеризующей относительную величину реакции электрической цепи в режиме постоянного тока. В частных случаях значение этого предела может быть равно нулю.

В зависимости от типа реакции и типа воздействия (ток или напряжение) различают четыре вида переходных характеристик (рис. 1.1):

переходная характеристика по напряжению.

переходная характеристика по току.

переходная проводимость.

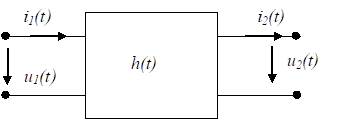
Рис. 1.1

Рассмотрим линейную электрическую цепь, не содержащую независимых источников тока и напряжения. Пусть внешнее воздействие на цепь представляет собой неединичный скачок x (t)=x¹(t)=X*1 (t-t₀), а реакция цепи на это воздействие при нулевых начальных условиях y (t)=y¹(t).

Тогда переходная характеристика цепи.

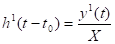
(1.2).

Из выражения (1.1) видим, что h¹(t-t₀)=y¹(t), если Х=1, следовательно, переходная характеристика цепи численно равна реакции цепи на воздействие единичного скачка тока или напряжения.

Пусть внешнее воздействие на цепь задается в виде произвольной функции х=х (t), равной нулю при t 0 и непрерывной при всех t, за исключением точки t=t₀. Эту функцию можно приближенно представить в виде суммы неединичных скачков. Тогда, в соответствии с определением переходной характеристики (1.2), реакция цепи на воздействие неединичного скачка, приложенного в момент времени t равна произведению высоты скачка на переходную характеристику цепи. Следовательно, реакция цепи на воздействие, представляемое суммой неединичных скачков, равна сумме произведений высот скачков на соответствующие переходные характеристики:

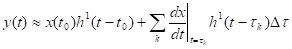
(1.3).

Точность представления входного воздействия в виде суммы неединичных скачков, как и точность представления реакции цепи в виде (1.3), возрастает с уменьшением шага разбиения по времени? ф. При? ф >0 суммирование заменяется интегрированием:

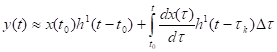
(1.4).

Используя это выражение, которое известно под названием интеграл Дюамеля, можно найти точное значение реакции цепи на заданное воздействие х=х (t) в любой момент времени t после коммутации.