Случай идеального газа

Идеальным газом называется газ, для которого справедливо уравнение состояния.

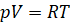
(26).

где p — давление, V—объем одного моля, R—универсальная газовая постоянная, T—температура, измеренная по термодинамической шкале («абсолютная температура»), или.

.

где М— масса 1 моля, с= M/V— плотность.

Воздух, кислород, азот, водород и многие другие газы при комнатной температуре и давлении порядка атмосферного можно рассматривать с достаточным для акустики приближением как идеальные газы.

Как учит термодинамика, в случае идеального газа соотношение (2.17) имеет вид:

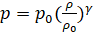
(27).

Где.

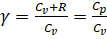
постоянная величина (и — теплоемкости газа соответственно при постоянном давлении и постоянном объеме). Следовательно, здесь.

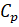
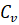
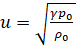
(28).

Еще задолго до Пуассона вопросом о скорости звука в воздухе занимался Ньютон. Он считал, что.

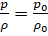
(27а) т. е. не учитывал изменения температуры воздуха при распространении в нем звуковой волны, вследствие чего получил для скорости звука соотношение.

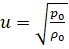
(28а) Это соотношение можно получить из уравнения (25), подставляя в него (27а) вместо (27).

Количественно-качественное сравнение теорий Ньютона и Пуассона

Произведем сравнение результатов, полученных путем применения формул (28) и (28а) — уравнений Ньютона и Пуассона.

Подсчитаем для воздуха: =1,4; с = 1,29 при комнатной температуре (20° С, Т =293 К) формула Ньютона дает u =290 м/сек, формула Пуассона u=331 м/сек. Формула Пуассона хорошо подтверждается на опыте и для других газов (но крайней мере при не очень высоких частотах):

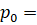
1)для гелия =1,7; с =0,179 при температуре 0 °C, Т=273 К, давление 101 325 Па формула Ньютона: u = 752 м/сек формула Пуассона: u=980 м/сек.

2)для аммиака.

=1,3; с =0,77 при температуре 0 °C, Т=273 К, давление 101 325 Па формула Ньютона: u = 362 м/сек формула Пуассона: u=413 м/сек.

3)для углекислого газа.

=1,2; с =1,98 при температуре 0 °C, Т=273 К, давление 101 325 Па формула Ньютона: u = 226 м/сек формула Пуассона: u=250 м/сек Этим оправдывается предположение о том, что сжатие и разрежение газа в звуковой волне являются практически адиабатическими процессами.

Как видно из результатов, полученные значения скорости звука из разных формул в одном случае небольшая (для углекислого газа всего 24 м/с), а в другом случае довольно значительная (для гелия она составляет 228 м/с).

Это происходит потому, что количество степеней свободы этих газов различно.

Так как, где i-количество степеней свободы молекул газа Для одноатомного идеального газа (гелий) i=3, т. е.

.

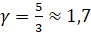
Отсюда и большая разница в расчетах при использовании двух разных формул, чем, например, для кислорода двухатомного газа (i=5):

.

То есть квадратный корень из 1,7 будет больше, чем из 1,4. Соответственно, чем большим количеством степеней свободы обладает газ, тем меньше разница, полученная при расчетах по разным формулам.