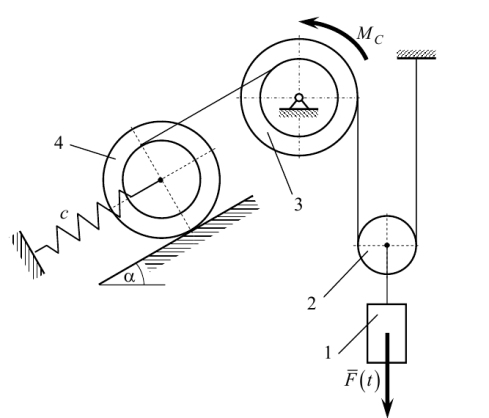
Исследование колебаний механической системы с одной степенью свободы

II. Определение закона движения системы Проинтегрируем дифференциальное уравнение (1.20).

Общее решение S неоднородного дифференциального уравнения (1.20) складывается из общего решения однородного уравнения S_OD и частного решения S_Ч неоднородного: S = S_OD + S_Ч.

Однородное дифференциальное уравнение, соответствующее данному неоднородному (1.20), имеет вид:

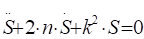
(2.2).

Решение этого уравнения ищем в виде функции.

S = Ae^Lt, (2.3).

где, А и L неопределенные постоянные величины.

Подставляя (2.3) в (2.2), получаем:

(L² + 2nL + k²) Ae^Lt = 0.

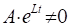
Так как мы ищем нетривиальное решение, то. Следовательно, должно выполняться условие.

L² + 2nL + k² = 0. (2.4).

Уравнение (2.4) называется характеристическим уравнением дифференциального уравнения (2.2). Эти уравнение имеет два корня:

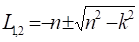
(2.5).

n < к, поэтому общее решение уравнения (2.2) имеет вид:

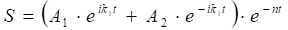
(2.6).

где А₁, А₂ постоянные интегрирования,.

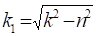
(2.7).

k₁ = 3,06 c^-1

Решение (2.6), используя известные формулы Эйлера.

.

нетрудно представить в виде:

S_{OD =} (2.8).

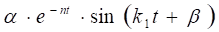
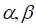
где постоянные интегрирования.

Определим частное решение неоднородного дифференциального уравнения.

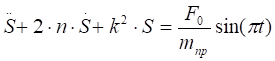
(2.9).

Частное решение ищем в виде правой части.

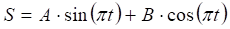
(2.10).

Подставляя (2.10) в (2.9), после несложных преобразований получаем:

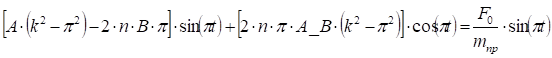
Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных, А и В:

.

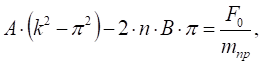
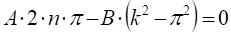
Решая эту систему, получаем следующие выражения для коэффициентов, А и В:

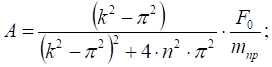
(2.11).

.

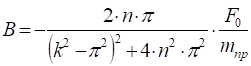
F₀ = 20 H, m_пр = 3.68 кг, k = 3.06 c^-1, n = 0.14 c^-1, .

A = -2,64 м.

B = 4,68 м Таким образом, решение (2.10) определено. Складывая (2.8) и (2.10), получаем общее решение неоднородного уравнения (2.9).

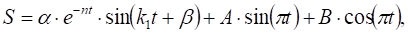
(2.12).

Константы определяются из начальных условий (1.21). Для этого найдем производную по времени от (2.12).

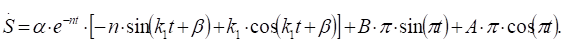
(2.13).

Подчинив (2.12) и (2.13) начальным условиям, получим систему уравнений относительно искомых констант.

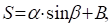
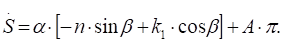
Решая эту систему, получаем:

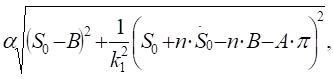
. (2.14).

б = 5,54.

tg в = 1,6.

в = arctg (1,6) = 58.

Подставляя (2.14) в (2.12), получаем закон движения механизма.

S = 5,54 е^-0,14t sin (0,36t+1,6) -2,64 sin (рt)+ 4,68cos (рt).

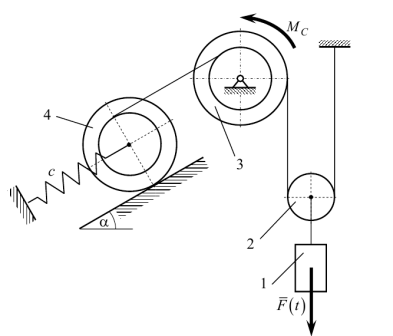
III. Определение реакций внешних и внутренних связей Для решения этой задачи расчленяем механизм на отдельные части и изображаем расчетные схемы отдельно для каждого тела (рис.3).

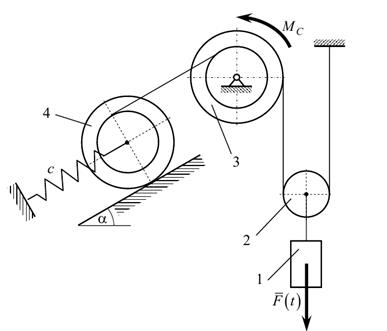
Рис. 3. Расчетные схемы каждого тела механизма

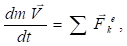
Определение реакций связей проведем с помощью теоремы об изменении количества движения и теоремы об изменении кинетического момента относительно центра масс.

(3.1).

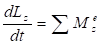
(3.2).

В соответствии с расчетными схемами (рис.2) записываем уравнения (3.1) и (3.2) в проекциях на оси координат.

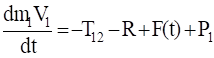
тело 1:, (3.3).

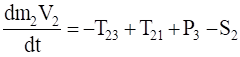
тело 2:, (3.4).

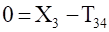
3, (3.5).

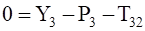
(3.6).

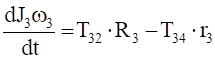
(3.7).

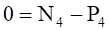
(3.8).

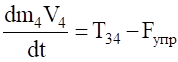
. (3.9).

С учетом кинематических соотношений (1.7) систему уравнений (3.3) (3.9) преобразуем к виду:

.

.

.

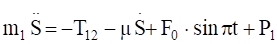
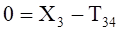
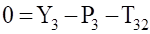
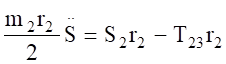
(3.10).

.

.

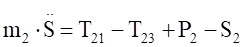
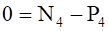
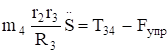
Уравнения (3.10) составляют систему алгебраических уравнений относительно функций: N₄, T₃₄, T₁₂, T_23, X₃, Y₃.

Решая эту систему, получаем и дифференциальное уравнение движения системы, и выражения для определения реакций.

.

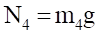
X₃=,.

.

.

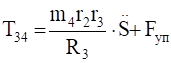
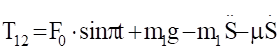
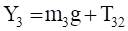
T₃₂₌

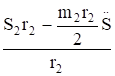
IV. Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа Общее уравнение динамики системы есть математическое выражение принципа Даламбера-Лагранжа.

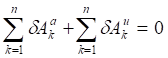
. (4.1).

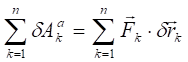
Здесь сумма элементарных работ всех активных сил на возможном перемещении системы;

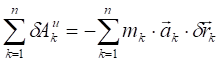
сумма элементарных работ всех сил инерции на возможном перемещении системы.

Изобразим на рисунке активные силы и силы инерции (рис.4).

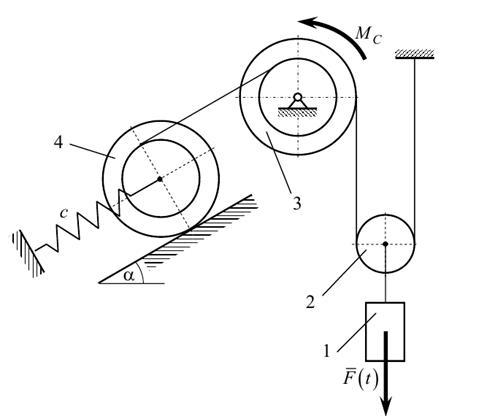
Рис. 4. Расчетная схема

Идеальные связи не учитывают и не отображают на расчетной схеме, поскольку по определению работа их реакций ва любом возможном перемещении системы равна нулю. Пружина является неидеальной связью. Введем реакцию этой связи в число активных сил.

Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:

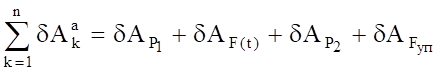
(4.2).

Вычисляя последовательно элементарные работы активных сил и суммируя их, получаем после несложных преобразований.

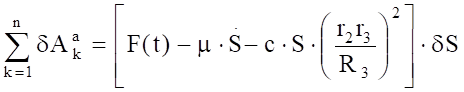
(4.3).

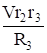
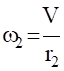
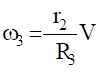
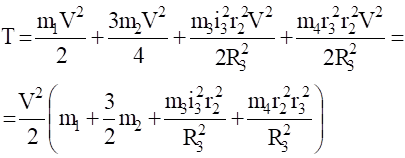
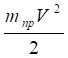
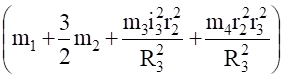
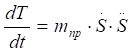
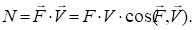
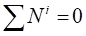
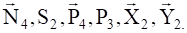
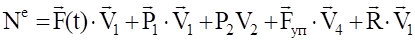
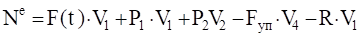
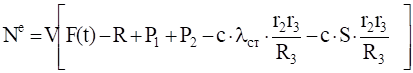
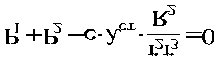
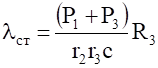
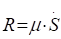
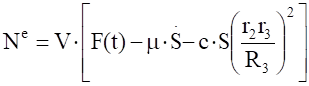
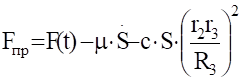
Аналогичное выражение для приведенной силы F_пр получено ранее [см. (1.18)].

Найдем возможную работу сил инерции:

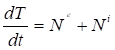
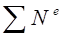
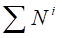
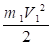
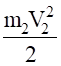
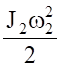
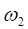
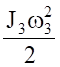
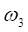
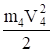
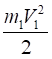
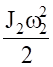
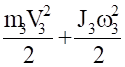
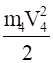
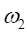
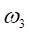
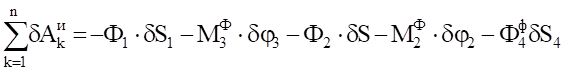
(4.4).

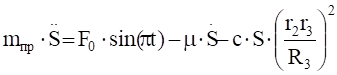
Для величин главных векторов и главных моментов сил инерции имеем следующие выражения:

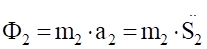
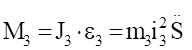
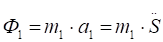
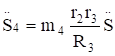
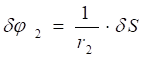
Ф₄=m₄ (4.5).

Используя кинематические соотношения (1.7), можно записать.

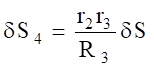
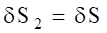
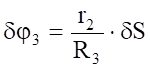
(4.6).

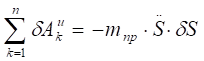
Тогда возможную работу сил инерции можно преобразовать к виду.

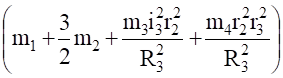
(4.7).

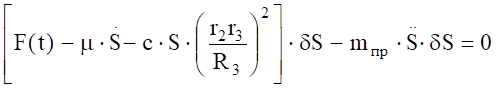
m_пр=, (4.8).

Аналогичное выражение для приведенной массы системы было получено ранее [см.(1.10)]. Подставляя выражения (4.3) и (4.8) в общее уравнение динамики (4.1), получаем.

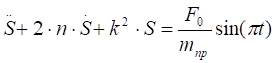
(4.9).

Поделив (3.10) на, получим дифференциальное уравнение вынужденных колебаний системы:

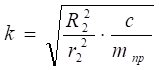
(4.10).

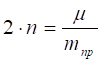
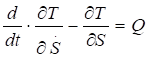
(4.11).

Дифференциальное уравнение (4.10) полностью совпадает с полученным ранее уравнением (1.20).

V. Составление дифференциального уравнения движения механизма с помощью уравнений Лагранжа 2-го рода.

Составим теперь уравнения Лагранжа 2-го рода. Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид:

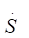
(5.1).

где Т кинетическая энергия системы;

Q обобщенная сила;

S обобщенная координата;

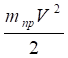
обобщенная скорость. Выражение для кинетической энергии системы было найдено ранее (1.9):

T=,.

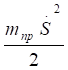
m_пр=,.

Учитывая, что V =, получаем.

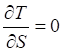
T=, (5.2).

Производные от кинетической энергии.

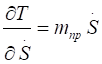
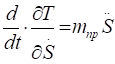
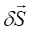
;;. (5.3).

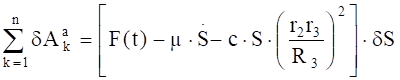
Для определения обобщенной силы Q сообщим системе возможное перемещение (рис. 3) и вычислим сумму элементарных работ всех активных сил на возможных перемещениях точек их приложения [см. (3.3)]:

.

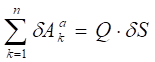
С другой стороны для системы с одной степенью свободы.

(5.4).

Сравнивая два последних соотношения, получаем.

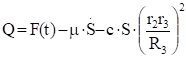
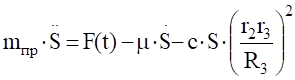
(5.5).

Подставляя производные от кинетической энергии (5.3) и обобщенную силу (3.16) в уравнение Лагранжа, получаем.

(5.6).

VI. Результаты вычислений Студентка: Пашута А. А. Группа: Б360 811.

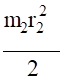
Вариант: 1.

с = 2000 Н/м m₁ = 2 кг m₂ = 1 кг m₃ = 3 кг m₄ = 4 кг.

f_ст = F'_сц =.

m_пр = 3,68 кг k = 3,06 c^-1 n = 0,14 c^-1 k₁ = 3,1 c^-1

A₀ = -2,64 м б₀ = 5,54.

B₀ = 4,68 м в₀ = 58.

Приложение.

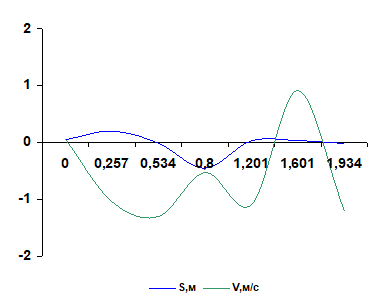
График зависимости S (t), V (t).

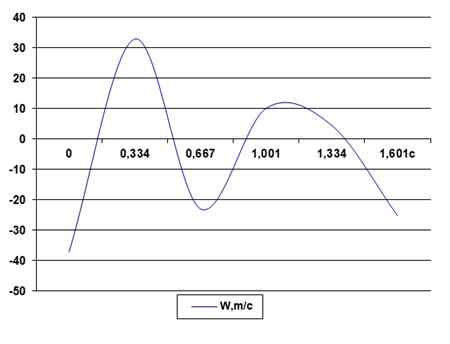
График зависимости W (t).

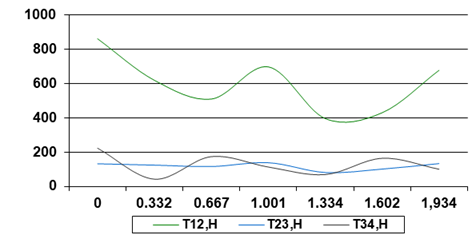
График зависимости T₁₂(t), T₂₃(t), T₃₄(t).