Электромагнитные волны. 
Электромагнитные волны

Плоская электромагнитная волна и ее параметры

Электромагнитную волну называют плоской, если и электрическое, и магнитное поле не изменяется в плоскости перпендикулярной направлению распространения. Выражение для плоской волны удобно искать в прямоугольной системе координат (х, у, z). Пусть плоская волна распространяется вдоль оси z, то есть вектор Пойнтинга имеет единственную проекцию П_z, которую можно найти, спроектировав выражение (2.23).

на ось z. Запишем это равенство в проекциях на координатные оси. Известно, что векторное произведение двух векторов можно представить в виде определителя квадратной матрицы (см. приложение).

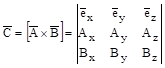
(3.1).

Воспользуемся этим равенством для того, чтобы переписать правую часть (2.23) в виде квадратной матрицы.

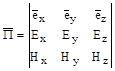
Разложим определитель на миноры по первой строке.

(3.2).

Отлично от нуля только третье слагаемое (проекция вектора Пойнтинга на ось z), которое содержит только поперечные составляющие полей. Поэтому в плоской волне нет ни электрического, ни магнитного поля в направлении распространения волны — электромагнитная волна поперечная. Чтобы упростить анализ направим ось х вдоль направления вектора. Тогда электрическое поле будет иметь единственную проекцию E_х. Воспользуемся уравнением Гельмгольца для электрического поля (см. 2.2.1).

.

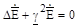
Спроектируем это уравнение на ось х.

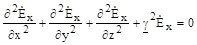
. (3.3).

Электрическое поле в плоской волне не зависит от поперечных координат х и у, поэтому первое и второе слагаемые равны нулю. Тогда вместо (3.3) можно записать:

Это обыкновенное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение хорошо известно. Его можно представить тремя способами: в виде суммы двух мнимых экспонент, суммы синуса и косинуса с различными амплитудами и в виде Asin (z+), где, А и — произвольные постоянные. Для плоских волн решение представляют в виде суммы двух мнимых экспонент.

(3.4).

Теперь рассчитаем магнитное поле. Можно воспользоваться уравнением Гельмгольца для магнитного поля, но тогда появится еще две произвольные постоянные и их нужно будет определять. Поэтому более рационально использовать уравнение Максвелла для ротора электрического поля и определить магнитное поле через электрическое, для которого решение уже получено. Распишем первое уравнение (2.1.4) с нулевой плотностью магнитного тока.

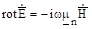
в координатах. Для этого представим rot в виде векторного произведения вектора на и, воспользовавшись (3.2), получим.

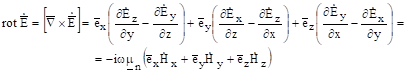
Учтем, что вектор имеет единственную проекцию на ось х и эта проекция не зависит от поперечных координат. Тогда в уравнении останется единственное слагаемое, проекция на ось у, и последнее равенство можно переписать в виде.

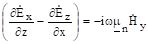
Подставим Ё_х из выражения (3.4) и получим единственную проекцию магнитного поля:

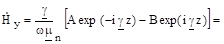
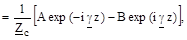
(3.5).

где Z_с = / - волновое сопротивление среды. Воспользуемся выражением для постоянной распространения (см. 2.12) и упростим выражение для волнового сопротивления.

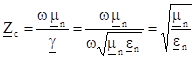
(3.6).

Итак, рассчитано электрическое и магнитное поле в плоской волне. Оба поля имеют по одной проекции в плоскости, перпендикулярной направлению распространения. У обоих полей в показатель экспоненты входит сомножитель, который называют постоянной распространения. Электрическое и магнитное поле связаны между собой через волновое сопротивление. Представим комплексную постоянную распространения в алгебраическом виде, но, следуя общепринятым обозначениям, знак перед мнимой частью выберем отрицательный.

(3.7).

и запишем выражения для и с учетом этого обозначения.

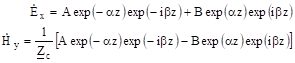
(3.8).

Перейдем от символического изображения, которое было использовано для упрощения расчетов, к выражениям для полей, как функций времени. Для этого воспользуемся стандартной методикой преобразования, которая состоит в следующем.

Сначала комплексная амплитуда преобразовывается в мгновенный комплекс, для чего ее умножают на exp (it). Затем от мгновенного комплекса берется действительная часть. Это и будет выражение для электрического или магнитного поля как функции времени. Проделаем эту процедуру для поля в плоской волне (3.8).

Проведя аналогичные расчеты для магнитного поля, получим:

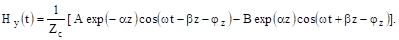
У обоих полей с ростом z амплитуда первого слагаемого падает, а второго растет. Первое слагаемое можно считать электромагнитной волной, распространяющейся вдоль положительного направления оси z. Амплитуда этой волны экспоненциально уменьшается по мере распространения. Второе слагаемое — это волна, распространяющаяся в обратном направлении, то есть вдольz, из бесконечности в начало координат. Действительно, если не обращать внимания на постоянный коэффициент, то второе слагаемое можно получить из первого, заменив z наz. Первому слагаемому соответствует прямая волна. Если на пути распространения волна встретит какую-либо преграду, то от нее она полностью или частично отразится и возникнет отраженная волна, описываемая вторым слагаемым.

Для прямой волны.

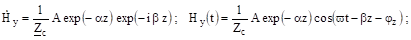
(3.9).

Для обратной волны:

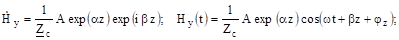
(3.10).

Если систему координат выбрать так, что электрическое поле направлено по оси у (=), то магнитное будет направлено по оси х и связь _y и _x останется прежней с точностью до знака.

Рассмотрим параметры, которые входят в выражения для полей плоской волны, как функций времени. Выражение для E_x(t) и H_y(t) можно разделить на две части. Ту часть, которая стоит перед косинусом, называют амплитудой электрического или магнитного поля. Амплитуда экспоненциально уменьшается с ростом координаты z. Коэффициент, стоящий в показателе экспоненты перед z, называют постоянной затухания. Аргумент косинуса называют фазой плоской волны. Для прямой волны.

(3.11).

Фаза — функция двух переменных: координаты и времени. Поверхность, для которой фаза постоянна, называется волновым фронтом. Как и следовало ожидать, у плоской волны волновой фронт — плоскость перпендикулярная оси z, вдоль которой волна распространяется. Скорость, с которой распространяется фронт волны, называется фазовой скоростью.

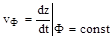
Чтобы определить фазовую скорость, зафиксируем фазу Ф =?t-z?=?const, и продифференцируем это равенство по времени.

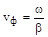
. (3.12).

Теперь определим параметры периодичности колебаний в плоской волне. Поскольку фаза зависит от двух переменных, то периодичность наблюдается и по времени и по координате. Период по времени так и называется периодом колебаний, а период по координате — длинной волны.

Определим период колебаний для плоской волны. Временная зависимость в плоской волне описывается косинусоидальной функцией, период которой составляет 2. Найдем разность фаз в моменты t и t +T в точке с координатой z ₀ и прировняем ее 2.

(3.13).

Теперь определим длину волны. Зафиксируем время и найдем такое приращение пространственной координаты, при котором фаза изменится на 2.

(3.14).

Величина показывает, сколько длин волн укладывается в 2 метрах и называется волновым числом. Если в (3.14) подставить волновое число из (3.12), то получим выражение, связывающее длину волны и период Длина волны, это то расстояние, которое электромагнитная волна проходит за период.

До сих пор мы рассматривали плоскую волну, распространяющуюся вдоль оси z. Рассмотрим общий случай, когда плоская волна распространяется вдоль произвольной оси, не совпадающей с осью z координатной системы. Повернем систему координат (x, y, z) так, чтобы в новой системе координат (х, у, z) волна распространялась вдоль оси z. Тогда для плоской волны можно записать.

.

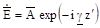
Здесь вектор расположен в плоскости, перпендикулярной направлению распространения. Волновые фронты в данном случае имеют вид бесконечные плоскостей, удовлетворяющих уравнению вида z = const. Требуется выразить величину z' через исходные координата х. у, z. Для этого заметим, что z является проекцией на ось распространения любого радиуса-вектора, который проведен из начала координат, а его конец расположен на волновом фронте.

z = ,.

где можно записать через координаты:

= x+y+z,.

а единичный вектор по направлению z через направляющие косинусы.

=cos + cos + cos,.

где, и — углы образуемые осью z с координатными осями х, у и z соответственно.

Запишем новую координату z через старые.

z= x? cos + y? cos + z? cos.

и подставим ее значение в выражение для плоской волны.

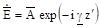
= (x?cos + y? cos + z? cos)}=.

=. (3.15).

В выражении (3.15) для сокращения записи введен волновой вектор

.