Несимметричные короткие замыкания

Основные уравнения

В расчетах несимметричных режимов используется метод симметричных составляющих. Для расчетных схем, содержащих синхронные машины, этот метод можно использовать при следующих условиях:

• — учитывается только основная гармоника токов и напряжений;
• — ЭДС, создаваемые протекающими в обмотках статора токами прямой, обратной и нулевой последовательностей, учитываются в виде падений напряжения с обратным знаком в соответствующих реактивностей СМ;
• — устройства АРВ реагируют только на отклонения напряжения прямой последовательности.

При этих условиях уравнения Кирхгофа для отдельных последовательностей:

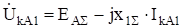
Эти уравнения записываются и решаются для особой фазы. За особую фазу принимают фазу А. Для решения этих уравнений следует добавить граничные условия.

Таким образом задача сводится к определению симметриных составляющих, по которым, используя известные соотношения, находят фазные токи и напряжения.

Параметры элементов для токов обратной и нудевой последовательностей

• — При отсутствии магнитной связи между фазами какого-либо элемента его сопротивления всех последовательностей одинаковы.
• — Для элементов, магнитносвязанные цепи которого неподвижны относительно друг друга равны между собой сопротивления прямой и обратной последовательностей.

Синхронные машины. Магнитный поток, созданный токами обратной последовательности, вращается относительно ротора с двойной синхронной частотой, встречая на своем пути периодически изменяющееся магнитное сопротивление, обусловленное магнитной и электрической несимметрией ротора. Соответственно изменяется и сопротивление обратной последовательности. Сопротивление обратной последовательности принимают.

.

При удаленном коротком замыкании:

.

.

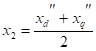
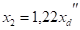
Магнитный поток статора нулевой последовательности в воздушном зазоре равен 0. Сопротивление нулевой последовательности определяется магнитным потоком рассеяния статора и составляет:

.

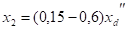
Асинхронный двигатель. В силу симметрии ротора АД для него принимают .

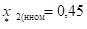
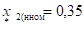
Обобщенная нагрузка. Сопротивление обратной последовательности обобщенной нагрузки следует принимать равным: при напряжении сети 35 кВ и более и при напряжении сети менее 35 кВ .

Сопротивление нулевой последовательности зависит от состава нагрузки и изменяется в широких пределах вплоть до .

Трансформаторы. Сопротивление нулевой последовательности трансформаторов определяется соединением его обмоток и конструкцией магнитопровода.

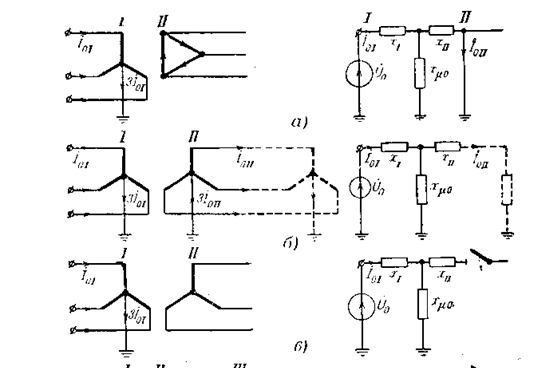
Со стороны обмотки, соединенной в треугольник или звезду с изолированной нейтралью, сопротивление нулевой последовательности бесконечно велико (х ₀ = 0), так как циркуляция тока нулевой последовательности в таком трансформаторе невозможна. Сопротивление нулевой последовательности имеет конечное значение только со стороны обмотки, соединенной в звезду с заземленной нейтралью.

Варианты соединения обмоток двухобмоточного трансформатора:

При соединении обмоток Y₀/ ЭДС нулевой последовательности трансформатора целиком расходуется на проведение тока нулевой последовательности через реактивность рассеяния обмотки, соединенной в треугольник, так как этот ток не выходит за пределы этой обмотки. В схеме замещения это отражается закорачиванием ветви с x_II. Это означает, что здесь заканчивается путь циркуляции тока нулевой последовательности.

При соединении обмоток Y₀/Y₀ предполагается, что на стороне обмотки II имеется еще одна заземленная нейтраль, т. е. обеспечен путь протекания тока нулевой последовательности. Если такой нейтрали нет, то схема замещения будет та же, что и для соединения обмоток Y₀/Y. Эта схема соответствует режиму холостого хода трансформатора.

Для группы из трех однофазных трансформаторов и для четырехили пятистержневых трансформаторов магнитные потоки нулевой последовательности замыкаются через свободные стержни. Ток намагничивания мал, и принимают, что x₀ = 0. В трехстержневых трансформаторах магнитные потоки нулевой последовательности замыкаются через среду с большим магнитным сопротивлением (изолирующую среду и корпус трансформатора). Для проведения этих потоков требуется значительный ток намагничивания, следовательно x₀ намного меньше x₁ (x₀ = 0,3−1,0).

Так как x₀ значительно больше x_II для трансформаторов любого типа с соединением обмоток Y₀/ принимают х _{2 = х 1.}

Для группы из трех однофазных трансформаторов и для четырехили пятистержневых трансформаторов:

при соединении обмоток Y₀/Y₀ х _{2 = хI +}

при соединении обмоток Y₀/Y х _{2 = .}

Для трех стержневых трансформаторов:

при соединении обмоток Y₀/Y

х _{2 = х 1 + x0}

при соединении обмоток Y₀/Y₀ трехлучевая схема замещения (по рисунку).

Трехобмоточные трансформаторы. У трехобмоточных трансформаторов одна из обмоток как правило соединена в треугольник. Д ля них принимают x_{0 = .}

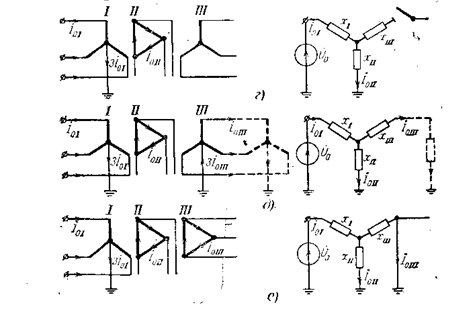
Рис. Трехлучевая схема замещения

x_{0 = xI + xII = xI-II}

x_{0 = xI + xII· xIII /(xII + xIII)}

Автотрансформаторы. Обмотки автотрансформатора связаны между собой не только магнитно, но и электрически. Поэтому в нем возможна циркуляция токов нулевой последовательности даже при изолированной нейтрали. Для двухобмоточного автотрансформатора сопротивление нулевой последовательности определяется суммарной реактивностью рассеяния его обмоток. Если автотрансформатор имеет третью обмотку, соединенную треугольником, он входит в общую схему замещения нулевой последовательности своей трехлучевой схемой замещения.

Воздушные линии. Рассмотрим участок линии, по которому протекает единичный ток. В этом случае сопротивление участка численно равно падению напряжения на этом участке.

При протекании тока прямой последовательности I_a = 1, I_b = a², I_c = a.

Z₁ = Z_L + a²Z_M + аz_M = Z_L — Z_M

Ток нулевой последовательности I_a = 1, I_b = 1, I_c = 1.

Z₀ = Z_L + Z_M + z_M = Z_L + 2Z_M

Таким образом, взаимоиндукция между фазами уменьшает сопротивление прямой и обратной последовательности и увеличивает сопротивление нулевой последовательности. Для двухцепных линий различие между х ₀ и х ₁ еще больше за счет взаимной индукции между проводами одной цепи и каждым проводом другой. Так для одноцепной линии без тросов х _{0/х 1 =3,5, для двухцепной — х 0/х 1 =5,5 на одну цепь.}

Заземленные с двух концов тросы уменьшают сопротивление нулевой последовательности ВЛ, так как тросы создают дополнительный путь для тока нулевой последовательности. Тросы, заземленные через искровые промежутки, никакого влияния на сопротивление нулевой последовательности ВЛ не оказывают.

При приближенных расчетах токов несимметричных КЗ допускается использовать данные о средних значениях отношений сопротивлений последовательности кабелей зависит от характера их прокладки, наличия или нулевой и прямой последовательностей ВЛ (приводятся в справочниках).

Кабели. Сопротивление нулевой последовательности кабелей зависит от характера их прокладки, наличия или отсутствия проводящей оболочки, сопротивления заземлений проводящей оболочки (если она имеется) и других факторов.

При приближенных расчетах токов несимметричных КЗ допустимо принимать:

.