Системный анализ решения задачи дискретной оптимизации на основе модифицированного бинарного алгоритма летучих мышей

Аннотация

Целью представленной работы является проведение системного анализа статистических сведений о результатах применения модифицированного бинарного алгоритма летучих мышей при решении динамических задач дискретной оптимизации для выявления особенностей его применения и уточнения правил настройки. В статье выполнено обоснование широкого применения алгоритмов агентных метаэвристик в решении оптимизационных задач. На уровне математической постановки показана одна из актуальных задач, решение которой востребовано на настоящий момент. Показанная задача интерпретирована на конкретном примере в терминах теории графов. Для её решения обоснованно выбран и модифицирован бинарный алгоритм летучих мышей, который позволил успешно решить указанную задачу. Последнее подтверждается представленными результатами трёх серий экспериментов. Авторами выполнен детальный анализ указанных результатов, материалы которого является основной частью работы. В заключении статьи сформирован перечень конкретных рекомендаций по повышению эффективности бинарного алгоритма летучих мышей для решения динамических задач дискретной оптимизации в целом.

Ключевые слова: системный анализ, дискретная оптимизация, теория графов, динамические задачи дискретной оптимизации, агентные метаэвристики, алгоритм летучих мышей.

Анализ алгоритмов агентных метаэвристик позволил выявить, что они являются алгоритмами коллективного поведения децентрализованных, самоорганизующихся естественных или искусственных систем. Классификация метаэвристик предполагает их деление на: эволюционные, вдохновлённые живой природой, вдохновлённые неживой природой и прочие [1, 2].

Данные метаэвристики нашли широкое применение в решении оптимизационных задач, общая постановка которых предполагает нахождение допустимого множества решений. Это множество на практике может быть и конечным, но его мощность зачастую настолько велика, что методы перебора в решении становятся неэффективными [3, 4].

Цель. Целью работы является системный анализ статистических сведений о результатах применения модифицированного бинарного алгоритма летучих мышей при решении динамических задач дискретной оптимизации для выявления особенностей его применения и уточнения правил настройки.

Материалы и методы исследования

Существует ряд задач из различных предметных областей, для которых существует актуальная востребованность в их решении на уровне следующей постановки задачи [5, 6]:

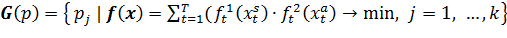
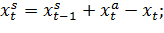
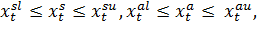
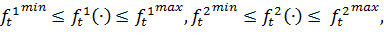
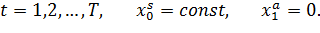
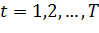
Интерпретация данной задачи возможна с учётом следующих допущений на примере прокладки маршрута между двумя удалёнными планетами p0 и pn в комическом пространстве. Примем во внимание, что для получения дополнительного разгона (и сокращения издержек по расходу топлива) за счёт известного «эффекта пращи» [7] полёт космического аппарата проходит мимо n-1 промежуточных планет с целью выполнения около них соответствующих гравитационных маневров. Полёт будет проходить на протяжении T (T? n) временных интервалов (каждый из которых соответствует перелёту между двумя планетами pj и pj+1). Абстрагируясь от деталей, будем считать, что переменными являются усреднённые значения собственной скорости космического аппарата на интервале t и скорости, полученной дополнительно в начале этого периода. Также предположим, что для каждого временного интервала известно неотрицательное значение снижения скорости .

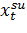
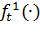
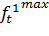
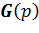
В соответствии с техническими требованиями, в каждом периоде собственная скорость космического аппарата должна быть не менее и не более единиц измерения, а интервал возможного изменения дополнительной скорости располагается соответственно между и. Логично предположить, что эти параметры неотрицательны (скорость должна быть достаточно велика, чтобы не возымел эффект падения космического аппарата на одну из планет). Ради простоты будем считать, что в начале межпланетного перелёта собственная скорость задана положительной константой из интервала, а первый импульс дополнительной скорости можно получить, только начиная с маневра около планеты p1 (т.е. в начале 2-го периода). Также предположим, что известны некоторые вогнутые функции и, первая из которых определяет длительность времени межпланетного перелёта в периоде t, (или длину траектории от pj до pj+1), а вторая — средний объём расхода топлива в единицу времени (или на единицу расстояния) в зависимости от. Важно отметить, что указанные функции имеют соответствующие ограничения иснизу и и сверху на области допустимых значений.

Скорость в начале периода t получается, очевидно, из скорости предыдущего периода прибавлением дополнительно полученной скорости в t-м периоде, а также вычитанием издержек снижения скорости в этом периоде.

Цель описанного процесса состоит в получении такого межпланетного маршрута, который удовлетворял бы всем ограничениям и минимизировал суммарные затраты при реализации данного перелёта.

Решение описанной динамической задачи дискретной оптимизации было изначально получено на основе бинарного алгоритма роя частиц. В последствии было выяснено, что алгоритм летучих мышей имеет ряд существенных преимуществ перед алгоритмом роя частиц, как по скорости выполнения, так и по мощности [5, 8].

Основные шаги алгоритма летучих мышей — это инициализация их популяции, миграция агентов, локальный поиск, глобальный поиск, эволюция параметров алгоритма и окончание итераций. С помощью эхолокации все мыши могут измерять расстояние до добычи и препятствий и могут различать их. Мыши движутся случайным образом, генерируя сигналы с определённой частотой и громкостью. В процессе поиска мыши могут менять частоту сигналов, а также частоту повторения излучаемых импульсов. Частота и громкость изменяются в определённых пределах [9].

дисктерный оптимизация бинарный алгоритм Результаты исследования и их обсуждение Для проведения экспериментов был модифицирован бинарный алгоритм летучих мышей [5, 8] Сейдали Маджалили (Seyedali Mirjalili) [10]. Ниже приведён фрагмент листинга программы, содержащий один из вариантов представления планет в двумерном пространстве с указанием значений для инициализации параметров алгоритма.

n = 25; % Размер популяции (обычно в пределах от 10 до 25).

A = .25; % Громкость.

r = .1; % Частота повторения импульсов.

Max_iter = 80; % Количество итераций.

% список планет с координатами (последняя «координата» — Xa ;

% дополнительная скорость от эффекта пращи.

% для 1-й планеты Xa = 0, для последней Xa = -1).

planets = [[1,20,0]; [3,15,2]; [5,17,1]; [5,15,1]; [5,11,1] [3,13,1]; [5,13,1]; [7,13,1]; [7,11,1]; [9,11,1] [7,7,1]; [5,5,1]; [7,5,1]; [7,3,1]; [9,3,4] [5,7,8]; [12,7,1]; [13,8,9]; [12,2,1]; [20,1,-1]];

Xs = 6; % Стартовая скорость корабля.

Xt = 1; % Скорость торможения корабля в пространстве.

d = length (planets); % Количество планет (искомых переменных) Результат работы алгоритма получается в виде двоичного вектора, представляющего последовательность планет от p0 до pn, входящих в итоговый маршрут (в соответствии с задачей о прокладке маршрута между двумя удалёнными планетами). Помимо этого, результат представляется графически и для каждого варианта получения маршрута строится график его сходимости к лучшему результату.

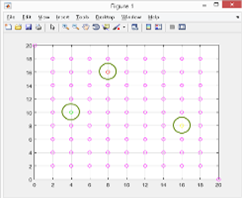
Эксперименты проводились на множестве планет с n = 83 в системе 2D (с целью облегчения анализа получаемых результатов) при равном удалении планет друг от друга и использовании цветовой нотации для отображения количественных характеристик в отношении возможно-получаемой дополнительной скорости от эффекта пращи (в условных единицах) для каждой из планет (рис.1): фиолетовая — дополнительная скорость = 1; зелёная — от 1 до 5; жёлтая — от 5 до 10; красная — от 10 и более.

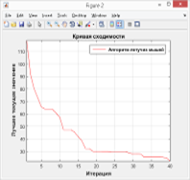
Рис. 1. — Изображение планет с применением цветовой нотации

Первая серия экспериментов проводилась при одинаковой дополнительной скорости для всех планет (3-я «координата»):

planets = [.

[0,20,0]; [2,18,1]; [4,18,1]; [6,18,1]; [8,18,1]; [10,18,1]; [12,18,1]; [14,18,1]; [16,18,1]; [18,18,1].

[2,16,1]; [4,16,1]; [6,16,1]; [8,16,1]; [10,16,1]; [12,16,1]; [14,16,1]; [16,16,1]; [18,16,1].

[2,14,1]; [4,14,1]; [6,14,1]; [8,14,1]; [10,14,1]; [12,14,1]; [14,14,1]; [16,14,1]; [18,14,1].

[2,12,1]; [4,12,1]; [6,12,1]; [8,12,1]; [10,12,1]; [12,12,1]; [14,12,1]; [16,12,1]; [18,12,1].

[2,10,1]; [4,10,1]; [6,10,1]; [8,10,1]; [10,10,1]; [12,10,1]; [14,10,1]; [16,10,1]; [18,10,1].

[2,8,1]; [4,8,1]; [6,8,1]; [8,8,1]; [10,8,1]; [12,8,1]; [14,8,1]; [16,8,1]; [18,8,1].

[2,6,1]; [4,6,1]; [6,6,1]; [8,6,1]; [10,6,1]; [12,6,1]; [14,6,1]; [16,6,1]; [18,6,1].

[2,4,1]; [4,4,1]; [6,4,1]; [8,4,1]; [10,4,1]; [12,4,1]; [14,4,1]; [16,4,1]; [18,4,1].

[2,2,1]; [4,2,1]; [6,2,1]; [8,2,1]; [10,2,1]; [12,2,1]; [14,2,1]; [16,2,1]; [18,2,1]; [20,0,-1]];

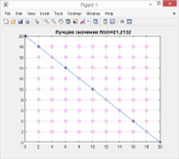
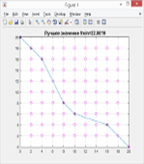
Очевидно, что в представленном случае для планет p0 и p82 с координатами [0,20] и [20,0] соответственно, оптимальный вариант траектории — это прямая, соединяющая эти планеты (возможно через некоторые промежуточные планеты). Результаты выполнения эксперимента, представленные на рис. 2. а, подтвердили данное предположение.

а б в.

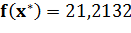
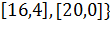
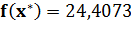
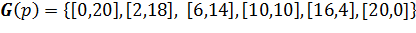
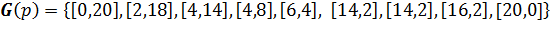
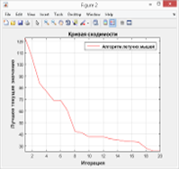
г д е Рис. 2. — Результаты первой серии экспериментов

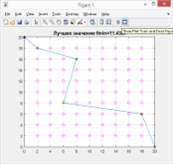
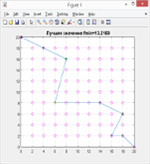
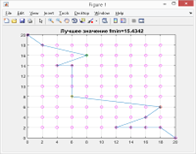
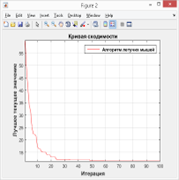
На рис. 2.а представлен результат эксперимента для 85 итераций, , на рис. 2. в — для 40 итераций, , и на рис. 2.д — для 20 итераций,. Планеты, помеченные крестиками — включенные по итогам работы алгоритма в соответствующие маршруты. На рис. 2.б, 2. г и 2. е показаны соответствующие графики сходимости алгоритма.

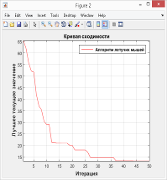
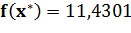
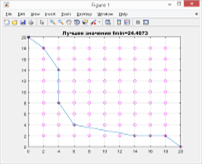
Вторая серия экспериментов проводилась при тех же значениях количества анализируемых планет и их удалённости друг от друга. При этом для планет с координатами [8,16], [6,8] и [18,6] были заданы различные повышенные значения дополнительной скорости, которую может получить космический аппарат, включив их в свой маршрут (выполняя около них соответствующий маневр). Для первой из указанных планет дополнительная скорость была задана в размере 4 условных единиц скорости, для второй и третьей — 8 и 15 соответственно.

Результаты второй серии экспериментов представлены на рис. 3.

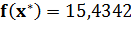
а б в.

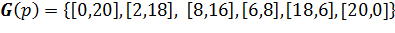
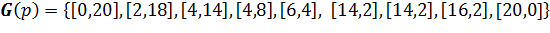
г д е Рис. 3. — Результаты второй серии экспериментов

На рис. 3. а представлен результат эксперимента для 100 итераций, на рис. 3. в — для 50 итераций,, и на рис. 3.д — для 20 итераций,. Планеты, включенные по итогам работы алгоритма в соответствующие маршруты, также помечены крестиками. На рис. 3. б, 3. г и 3. е показаны соответствующие графики сходимости алгоритма.

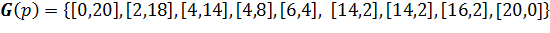
Из представленных результатов следует, что при снижении количества итераций алгоритма, качество получаемых результатов снижается пропорционально разнице между количеством итераций алгоритма и количеством анализируемых планет. При этом в экспериментах, для которых задавалось количество итераций больше количества анализируемых планет, качество получаемых результатов оставалось неизменным.

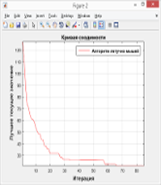
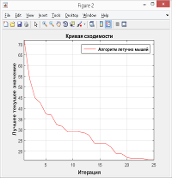
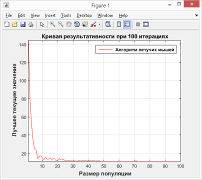
Последнее также было подтверждено результатами первого эксперимента в третьей серии: при исходных данных, таких же, как во второй серии экспериментов, посредством циклического изменения количества итераций был получен график зависимости качества решений (значений от количества итераций алгоритма (рис. 4).

Анализ графика указывает на то, что лучшие результаты вычислений с помощью бинарного алгоритма летучих мышей для решаемой задачи получаются при количестве итераций, примерно равном количеству анализируемых планет.

Аналогично первому эксперименту в третьей серии были проведены ещё три эксперимента: при фиксированном количестве итераций (83 итерации) были исследованы зависимости качества расчётных маршрутов (значений от размера популяции (рис. 5), громкости (рис. 6) и частоты повторения (рис. 7) излучаемых импульсов.

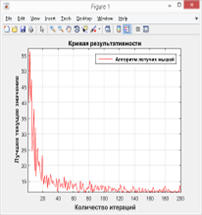
Рис. 4. — График зависимости качества решений от количества итераций алгоритма

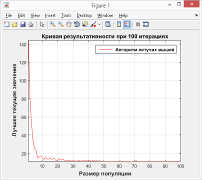
Рис. 5. — График зависимости качества решений от размера популяции

Анализ графика на рис. 5 подтверждает нецелесообразность использования популяций летучих мышей размерностью более 25 особей (качество результатов алгоритма при бо’льших значениях этого параметра остаётся неизменным). Данный результат подтверждает рекомендации автора классического алгоритма летучих мышей Xin-SheYang по определению размера популяции летучих мышей в пределах от 10 до 25 особей.

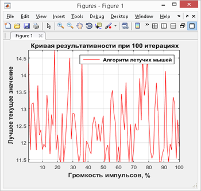
Анализ графика на рис. 6 позволяет утверждать, что громкость излучаемых импульсов практически не влияет на результативность бинарного алгоритма летучих мышей (на это указывает сильный разброс полученных расчётных значений).

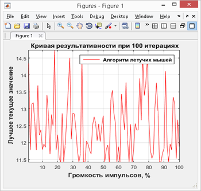
Рис. 6. — График зависимости качества решений от громкости излучаемых импульсов

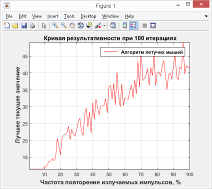
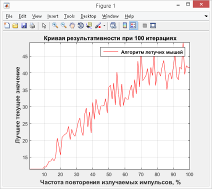
Рис. 7. — График зависимости качества решений от частоты повторения излучаемых импульсов

Кривая на графике с рис. 7 показывает на то, что при увеличении частоты повторения излучаемых импульсов летучих мышей выше значения 0,1 качество получаемых решений снижается пропорционально росту этого показателя. Очевидный вывод — значение данного параметра в алгоритме должно задаваться не более 0,1.

Заключение

В результате проведения трёх серий описанных экспериментов и анализа полученных результатов был сформирован перечень конкретных рекомендаций по повышению эффективности бинарного алгоритма летучих мышей для решения динамических задач дискретной оптимизации.

• 1. Для получения лучших результатов вычислений количество итераций алгоритма должно соответствовать размерности пространства поиска.
• 2. Размер популяции должен выбираться в пределах от 10 до 25 особей, что соответствует рекомендациям автора классического алгоритма летучих мышей (Xin-SheYang).
• 3. Громкость импульсов, излучаемых особями, практически не влияет на результативность бинарного алгоритма.
• 4. При увеличении частоты повторения излучаемых особями импульсов выше значения 0,1 качество получаемых решений снижается пропорционально росту этого показателя.

Рекомендация № 1 указывает на то, что при значительном увеличении размерности пространства поиска требуется модификация алгоритма с целью снижения количества итераций и сохранения качества его сходимости. В данном случае имеет смысл продолжить исследования в направлении возможной оптимизации свободных параметров для использованных алгоритмов на основе метода дробного исчисления [1, 3].

• 1. Дутова И. Г., Мохов В. А., Кузнецова А. В. и др. Метаоптимизация роя частиц на основе метода дробного исчисления // Современные проблемы науки и образования. 2015, № 2−1.
• 2. Есаулов В. А., Гринченков Д. В., Мохов В. А. Итерационный метод решения систем линейных уравнений с использованием q-градиента // Инженерный вестник Дона, 2015, № 3
• 3. Мохов В. А., Бородулина Е. Р. К вопросу о параметрической оптимизации роевых алгоритмов // Ростов-на-Дону: «Известия ЮФУ. Технические науки». 2014, № 4, С. 230−234.
• 4. Туровская Е. В., Мохов В. А., Кузнецова А. В. Моделирование процесса оптимального размещения товаров на складе самообслуживания на основе эволюционных алгоритмов поиска // Инженерный вестник Дона, 2014, № 1.
• 5. Мохов В. А., Туровская Е. В., Туровский Ф. А. Анализ бинарного алгоритма летучих мышей при решении задач дискретной оптимизации // Новая наука: от идеи к результату: Международное научное периодическое издание по итогам Международной научнопрактической конференции (Стерлитамак, 29 дек. 2015 г). — Стерлитамак: РИЦ АМИ, 2015, С. 101−103.
• 6. Мохов В. А., Туровский Ф. А. К вопросу о единообразии постановки некоторых задач дискретной оптимизации // Современный научный вестник, 2015, № 1, С. 41−45.
• 7. Овчинников М. Ю., Трофимов С. П., Широбоков М. Г. Метод виртуальных траекторий для проектирования межпланетных миссий с гравитационными маневрами // Препринты Института прикладной математики им. МВ Келдыша РАН, 2012, № 0, С. 9−26.
• 8. Гринченков Д. В., Мохов В. А., Пивоваров С. А. и др. Вариант реализации роевого алгоритма летучих мышей // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки, 2015, № 4, С. 22−27.
• 9. YangX. S., Hossein Gandomi A. Bat algorithm: a novel approach for global engineering optimization // Engineering Computations, 2012, № 5, pp. 464−483.
• 10. Mirjalili S., Mirjalili S.M., Yang X.S. Binary bat algorithm // Neural Computing and Applications, 2014, № 3−4, pp. 663−681.