Устойчивость плиты Э. Рейсснера на упругом невинклировом основании

Аннотация

Исследуется задача об устойчивости плиты Э. Рейсснера, лежащей на трехмерном упругом слое с заданными постоянными упругости. Торцевые поверхности слоя гладкие, связи удерживающие. Считается, что плита находится в плоском напряженно-деформированном состоянии от действия на ее цилиндрическую поверхность самоуравновешенной нагрузки с некоторым числовым параметром, характеризующим величину нагрузки при потере устойчивости плиты. Из условий удерживающих связей получена система уравнений для определения числового параметра. Дается метод вычисления наименьшего значения параметра, при котором фиксируется потеря устойчивости плиты. Как частные случаи, приводятся результаты классической теории и модель основания Винклера.

Ключевые слова: самоуравновешенная нагрузка, деформированное состояние, функции напряжений, потеря устойчивости.

устойчивость плита рейсснер нагрузка В настоящее время изучение проблем теории упругости является актуальной задачей [1,2]. Теория упругости — прикладная наука, обслуживающая разнообразные отрасли техники, где постоянно возникают вопросы о прочности и надежности конструкций, об их взаимодействиях с окружающей средой. Роль расчетов на прочность и жесткость становится все более ответственной, а сами расчеты — все более сложными.

Целью настоящей статьи является рассмотрение задачи об устойчивости плиты Э. Рейсснера, лежащей на трехмерном упругом слое с заданными постоянными упругости и как частные случаи, приводятся результаты классической теории и модель основания Винклера.

Рассмотрим плиту, имеющую форму и ограниченную цилиндрическим контуром Г, лежащую на упругом трехмерном слое: — (х, у) <; 0 z1 h1. Пусть упругие постоянные слоя Е1, 1, толщина плиты h, ее упругие постоянные Е, , D h3E/12(1- 2). Торцевые поверхности слоя гладкие, связи удерживающие. Предположим, что плита находится в плоском напряженно-деформированном состоянии от действия на контур Г самоуравновешенной нагрузки Pn (s), P (s), где — некоторый числовой параметр, характеризующий величину нагрузки при потере устойчивости плиты. Из перечисленных условий следует, что.

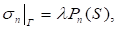
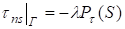
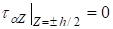
;; (1).

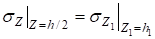
; (2), .

Пусть по какой-то причине плита несколько изогнулась. Рассмотрим условия бифуркации форм равновесия сжатой плиты по Эйлеру.

Если плита нагружена системой сил (1), то при ее изгибе сжимающие силы дают составляющую в том же направлении, что и поперечная нагрузка:

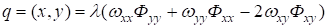
(4).

где — функция продольных усилий в плите, определяемая с помощью решения бигармонической проблемы [3]. Соотношения для силовых и геометрических характеристик в плите Э. Рейснера имеют вид.

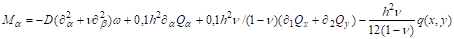
(5).

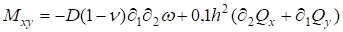
; (6).

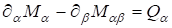
(7).

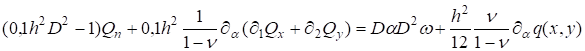
(8).

Напряженно-деформированное состояние упругого трехмерного слоя описывается решением однородных уравнений теории упругости в перемещениях [4]:

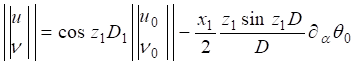
(9).

; (10).

(11).

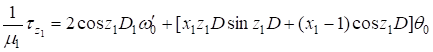
. (12).

Здесь, ,, , — основные искомые функции. Выражения (10), (11) тождественно удовлетворяют условиям (2). Остальные условия на торцах плиты и слоя позволяют решить задачу о бифуркации форм равновесия системы и определить значения параметра. С этой целью подставим (10) — (12) в (2) и (3). Получаем.

; (13).

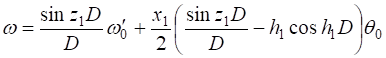
; (14).

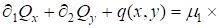
(15).

Таким образом, общее решение задачи о напряженно-деформированном состоянии системы «плита — слой» сводится к решению системы уравнений (8), (13) — (15). Преобразуем ее. Из (8) и (15) имеем.

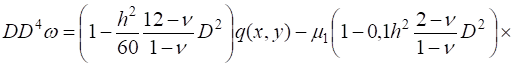
(16).

.

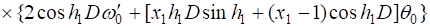
Подстановка (14) в (16) приводит к уравнению.

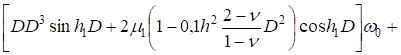
(17).

.

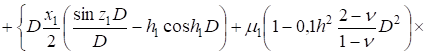
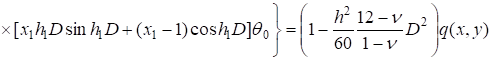
Далее весь вопрос заключается в решении системы уравнений (13), (17), которую можно построить полуобратным методом. Для этого представим искомое решение в виде суммы двух независимых решений — потенциального и вихревого. Легко показать, что вихревое решение не разрешает проблему устойчивости рассматриваемой системы «плита — слой», а потому остановимся только на потенциальном решении.

Пусть.

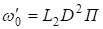
, , (18).

где L1 и L2 -некоторые дифференциальные операторы; П — функция напряжений.

Подставляя (18) в (13), приходим к уравнению.

.

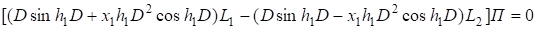
которое удовлетворим тождественно при очевидном выборе операторов:

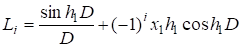
(20).

Искомые функции принимают вид

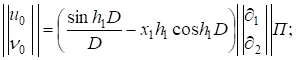
(21).

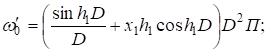
(22).

. (23).

Выражения для изгиба плиты находим из выражения (14):

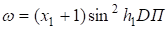
(24).

Дифференциальное уравнение для функции напряжений П получим после подстановки (22) — (24) в (17):

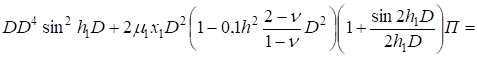
(25).

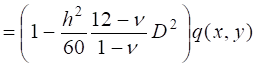
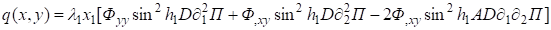
а бигармоническая функция — решение задачи о плоском напряженно-деформированном состоянии плиты [3].

В качестве примера рассмотрим случай равномерного сжатия плиты. Получаем.

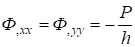
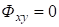
(27).

Уравнения (25) и выражение (26) принимает вид

(28).

;

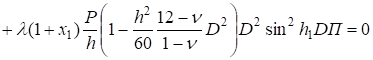
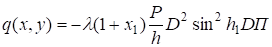
. (29).

Для решения широкого круга инженерных задач, связанных с проблемой потери устойчивости прямоугольных плит различного назначения, часто применяют метод, по которому задается некоторая форма прогиба плиты. Для шарнирно опертых плит такая форма принимается в виде.

(30).

а функция напряжений П определяется из дифференциального уравнения (24):

.

Частное решение этого уравнения имеет вид [2].

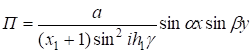
(31).

где .

После подстановки (31) в (28) получаем уравнение для :

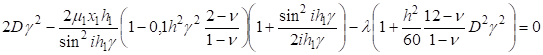
Наименьшее значение характеризует величину нагрузки на контуре Г, при которой фиксируется потеря устойчивости.

Прикладные теории.

1. Если плита Э. Рейснера оперта по контуру Г, то уравнения форм равновесия можно получить при и. Из (4) и (16) получаем

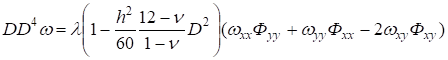
(33).

Силовые характеристики определяем по формулам (5) — (8). Отбрасывая член с h2, получаем результаты классической теории.

2. Если в разложениях дифференциальных операторов для слоя удерживать члены с, то получим модель основания Винклера. В случае равномерного сжатия плиты уравнения форм равновесия выглядят следующим образом:

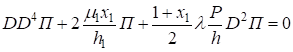
; (34).

(35).

В качестве примера рассмотрим выпучивание плиты размерами a? b. Предположим, что прогиб плиты и функция напряжений выражается в виде.

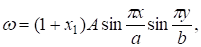
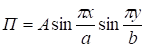
(36).

Подставляя (36) в (34), определим параметр для рассматриваемого выпучивания:

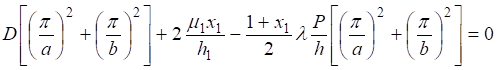
. (37).

Соотношения между размерами плиты установим с помощью условия равновесия.

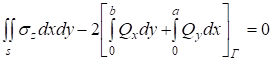
. (38).

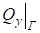
Так как перерезывающие силы, и контактное напряжение.

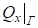
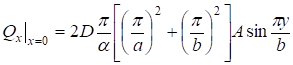
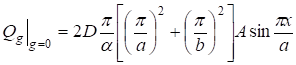
; (39).

; (40).

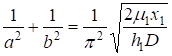
(41).

то, после интегрирования (38), получаем соотношение

. (42).

Из (37) и (41) можно получить более простую формулу:

.

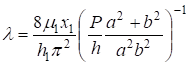
Таким образом, теория Э. Рейснера в нулевом приближении приводит к результатам классической теории. При этом выполнятся все краевые условия равновесия плиты. В этом достоинство рассматриваемого метода.

• 1. Беппаев А. М., Шогенов О. М. Оценка прочности железобетонной плиты на продавливание // Инженерный вестник Дона. 2016. № 2URL:ivdon.ru/magazine/archive/n2y2016/3671.
• 2. Кравченко Г. М., Труфанова Е. В., Вержиковский В. В., Заритовский В. С. Исследование напряженно-деформированного состояния фундаментной плиты выставочного павильона Технопарка РГСУ с учетом различных моделей основания// Инженерный вестник Дона. 2013. № 4 URL: ivdon.ru/ru/magazine/archive/n4y2015/3327
• 3. Тимошенко С. П., Войновский-Кригер С. Пластинки и оболочки. — М.: Физматгиз, 1963. — 635 с.
• 4. Лурье А. И. Пространственные задачи теории упругости. М., 1955. 492 с.
• 5. Лурье А. И. К теории толстых плит // ПММ. 1942. Т. 6. Вып. 2−3, С. 151−168.
• 6. Тр. Американского общества инж. -механ, 1969. Т. 36. № 4, С. 151−155.
• 7. Шарый С. П. Курс вычислительных методов. Новосибирск: Институт вычислительных технологий СО РАН, 2016. 526 с.
• 8. Воеводин В. В. Линейная алгебра. М.: Наука, 1980, 400 с.
• 9. Chen W.L., Striz A.G., Bert C.W. High-accuracy Plane Stress and Plate Elements in the Quadrature Element Method. International Journal of Solids and Structures. 2000, vol. 37, no. 4, pp. 627—647. URL: dx.doi.org/10.1016/S0020−7683 (99)00028−1.
• 10. Головина Л. И. Линейная алгебра и некоторые ее приложения. М., Наука, 1979. 392 с.
• 11. Wen P.H. The Fundamental Solution of Mindlin Plates Resting on an Elastic Foundation in the Laplace Domain and its Application. International Journal of Solids and Structures. 2008, vol. 45, no. 3, pp. 1032—1050. URL: dx.doi.org/10.1016/j.ijsolstr.2007.09.020.

References.

Kadomcev M.I., Ljapin A.A., Shatilov Ju.Ju. Inћenernyj vestnik Dona (Rus), 2012. № 3. URL: vdon.ru/magazine/archive/n3y2012/941/.

Zotov A.V., Ljapin A.A. Inћenernyj vestnik Dona (Rus), 2013. № 4. URL: ivdon.ru/ru/magazine/archive/n4y2013/2083/.

Lur’e A.I. Prostranstvennye zadachi teorii uprugosti. M., 1955, 492 p.

Lur’e A.I. PMM. 1942. T. 6. Vyp. 2−3, pp. 151−168.

Tr. Amerikanskogo obshhestva inzh.-mehan., 1969. T. 36. № 4, pp. 151−155.

Sharyj S.P. Kurs vychislitel’nyh metodov. [The course Computational Methods Novosibirsk: Institut vychislitel’nyh tehnologij]. SO RAN, 2016, 526 p.

Voevodin V.V. Linejnaja algebra [Linear algebra] M.: Nauka, 1980, 400 p.

Chen W.L., Striz A.G., Bert C.W. High-accuracy Plane Stress and Plate Elements in the Quadrature Element Method. International Journal of Solids and Structures. 2000, vol. 37, no.4, pp. 627—647. URL: dx.doi.org/10.1016/S0020−7683 (99)00028−1.

Golovina L.I. Linejnaja algebra i nekotorye ee prilozhenija [Linear algebra and some of its applications]. M., Nauka, 1979. 392 p.

Wen P.H. The Fundamental Solution of Mindlin Plates Resting on an Elastic Foundation in the Laplace Domain and its Application. International Journal of Solids and Structures. 2008, vol. 45, no. 3, pp. 1032—1050. URL: dx.doi.org/10.1016/j.ijsolstr.2007.09.020.