Inelastic impact of bodies

THE AIM: to study the laws of conservation of mechanical energy and impulse.

INSTRUMENTATION AND APPLIANCES: two metallic cylinders suspended to the light rods, angle scale.

Short theory of inelastic impact

The impact is the process of final alternation of velocities of bodies in a comparative short time. During perfectly inelastic impact when the forms and the sizes of bodies obtained during deformation remain after the stop of action of forces, perfectly plastic deformation takes place. The kinetic energy of the bodies motion partially transforms into heat and partially into kinetic energy. The system is closed (the work of the external forces is equal to zero) and dissipative. In such systems the law of conservation of the impulse accomplishes, but the law of conservation of mechanical energy doesn’t, because the part of energy converts into non-mechanical energy-heat. But the law of conservation of all kinds of energy for closed systems accomplishes. Let’s examine inelastic central impact (fig.13.1).

Figure 13.1.

The bodies move as whole body after the impact, it means that the velocity U of both bodies is the same. Let’s write down the equation of conservation of impulse and energy, taking into consideration that during the plastic deformation educes heat Q:

(13.1).

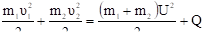
(13.2).

If we know masses of the bodies m1 and m2 and velocities V1 and V2 before the impact we can find the velocity U after the impact and the amount of heat Q.

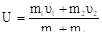
(13.3).

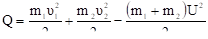
(13.4).

Consequence: If the masses of the bodies are the same and one of the bodies, for example the second is not moving (stable), then after the impact U=0,5v, it means that the velocity is twice reduced and the half of kinetic energy transfers into heat.

. (13.5).

In this work we examined inelastic impact of two bodies with the same mass which are suspended to the rods (fig.13.2). Inclination angles of the rods are measured by the scale. The masses of the bodies M, the rods m and the lengths of the rods L are the same.

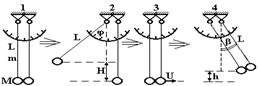
Figure 13.2.

During the inclination of the rod with the weight to the angle ф, the centre of the body weight lifts for H, and the centre of the weight of the rod for H/2. Their potential energy increases for such value.

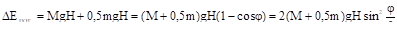
(13.6).

At the moment when a body passes low position, that means before the impact this potential energy in accordance to the law of conservation of mechanical energy (if don’t count the resistance of the air and the force of friction suspended), transforms into the kinetic energy of rotating body before the impact.

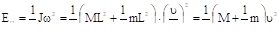
(13.7).

Where J is the sum of moments of inertia of the weight ML2 (as a material point) and of the rod? mL concerning the point of suspension;? is the angular velocity of rotation; v is the velocity of the weight before the impact.

After comparing the right parts of equations (13.6) and (13.7), we can find the velocity depending on the inclination angle.

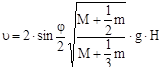
. (13.8).

After the impact the bodies move as whole body. So to find the velocity U and the kinetic energy E after the impact, in formulas (13.7) and (13.8) we should change M and m correspondingly into 2M and 2m, and the angle? into inclination angle? after the impact.

. (13.10).

The relative losses of mechanical energy for heat from equations (13.7)? (13.10).

(13.11).