Математическое описание технологического процесса изготовления канистры из полиэтилена низкого давления

Аннотация

Дано описание технологического процесса получения канистры из полиэтилена низкого давления. Приведены результаты исследований по определению зависимости входных технологических показателей от выходных показателей и характеристик изделия. Разработана математическая модель технологического процесса получения изделий из полиэтилена низкого давления. канистра полиэтилен давление низкий.

Ключевые слова: моделирование, системный анализ, экструдер, аппарат, функциональная схема, автоматизированное проектирование, нефтехимическая промышленность.

В современных условияхсоздание новых высокоэффективных технологических процессов, а также совершенствование уже действующих является одной из основных задач химической промышленности. Решение данной задачи возможно с помощью использования информационных технологий, а также совершенствования химико-технологических процессов [1,2]. Развитие систем автоматизированного проектирования обусловлено широким внедрением средств вычислительной техники и прикладного математического обеспечения. Основными преимуществами применения САПР, как известно, являются: повышение точности проектирования; снижение трудоемкости проектирования [3,4].

Существенная особенность химико-технологических процессов состоит в том, что совокупность составляющих их явлений носит детерминированно-стохастическую природу, проявляющуюся в особеностях процессов массопереноса, теплопереноса и химического превращения протекающих в технологическом оборудовании. Это объясняетсяслучайным взаимодействием составляющих компонентов или случайным характером граничных условий в оборудовании.

Решение проблемы изучения химико-технологических процессов возможно с помощью математического моделирования, базирующегося на системном анализе, который заключается в представлении анализируемого процесса как сложной взаимодействующей иерархической структуры с последующими качественным анализом ее структуры, разработкой математического описания и оценкой иследуемых параметров [5]. При рассмотрении явлений, возникающих в процессе движения различных частиц в сплошной жидкой среде, расматривают пять уровней:

• 1. Совокупность явлений на атомарно-молекулярном уровне;
• 2. Эффекты в масштабе надмолекулярных или глобулярных структур;
• 3. Множество физико-химических явлений, связанных с движением единичного включения дисперсной фазы, с учетом химических реакций и явлений межфазного энергопереноса и массопереноса;
• 4. Физико-химические процессыразличных включений, перемещающихся в сплошной фазе;
• 5. Совокупность процессов, определяющих макрогидродинамическую обстановку в масштабе технологического оборудования.

Для описание процесса применим математическое моделирование состоящее из трех этапов:

• 1. Составление математического описания исследуемого процесса или объекта;
• 2. Выборматематического описания и реализация его с помощью моделирующей программы;
• 3. Определение адекватности модели объекта.

На первом этапе выделяют основные явления и элементы в исследуемом процессе или объекте и затем устанавливают связи между ними. Далее, для каждого выделенного явления и элемента записывают уравнение, отражающее его функционирование. Также, в математическое описание включают уравнения связи между различными выделенными явлениями [6]. В нашем случае для описания технологического процесса изготовления канистры из полиэтилена низкого давления (ПНД) определяем технологические параметры процесса, такиекак:

• · Гранулы ПНД;
• · Краситель;
• · Охлаждающая жидкость;
• · Воздух;
• · Технические добавки.

Эти параметры существенно влияют на качество изготавливаемой канистры. В современном технологическом оборудовании поведение взаимодействующих частиц потока являеться являетьсясложным, поэтому дать строгое математическое описание в большинстве случаев не представляет возможным. Однако, структура потоков оказывает существенное влияние на эффективность химико-технологических процессов, поэтому при моделированни таких процессов ее необходимо учитывать. При этом математические модели структуры потоков являются основной, на которой строится математическое описание всего химико-технологического процесса [7].

При проведении химико-технологических процессов важно знать степень полноты ихзавершения, время пребывания частиц потока в аппарате и диффузию частиц, участвующих в химическом процессе [8].

Были проведены исследования по определению зависимости входных технологических показателей от выходных показателей и характеристик изделия на примере изготовления канистры из ПНД объемом 1 литр. Данные пассивного эксперимента процесса изготовления канистры объемом 1 литр представлены в таблице № 1. Были выявлены технологические показатели, наиболее влияющие на качество получаемой канистры.

Таблица 1.

Технологичекие показатели.

Распределение времени пребывания взаимодействующих частиц исследуемого потока в аппарате носит случайную природу и оценивается статистическим распределением. Наиболее важными источниками распределения элементов исследуемого потока по времени пребывания втехнологических аппаратах, используемых для изготовления данных изделий, являются:

• * нелинейность направлений скоростей системы;
• * турбулизация потоков;
• * наличие застойных областей в исследуемом потоке;
• * каналообразование, однонаправленные и перекрестные токи в системе;
• * температурные градиенты движущихся сред;
• * теплообмен и массообмен между фазами.

Все гидродинамические модели потоков записываются в виде уравнений, определяющих изменение концентрации веществ в них. Многообразие взаимодействующих диффузионных и тепловых потоков с учетом распределения по времени пребывания можно описать в виде следующих типовых математических моделей:

• * идеального смешения;
• * идеального вытеснения;
• * диффузионной;
• * ячеечной;
• * циркуляционной и комбинированной.

Выше приведенные модели отвечают следующим требованиям:

• * отражают основные физические закономерности реального потока;
• * позволяют экспериментально определять параметры модели;
• * дают возможность их использования для расчета конкретных технологических процессов.

Для описания технологического процесса изготовления канистры из ПНД предлагается ячеечная модель с обратными потоками, т.к. она наиболее точно отражает существующий технологический процесс. Согласно этой модели технологическое оборудование рассматривают как последовательность участков с сосредоточенными параметрами.

Рассматриваемая модель, впервые предложенная для каскада реакторов с мешалками, является одной из наиболее простых [9 — 12]. Согласно этой модели аппарат состоит из ряда последовательно соединенных ячеек, через которые проходит ис поток веществ, причем, в ячейки поток может попадать как прямой, так и обратный (рис.1).

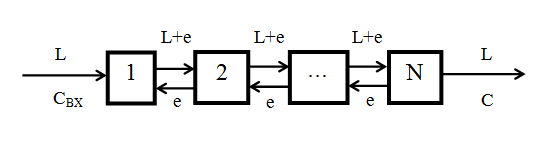
Рис. 1. — Функциональная схема ячеечной модели с обратными потоками

В качестве исследуемого параметра ячеечной модели, количественно характеризующим перемешивание, служит число ячеек полного перемешивания N.

Выражения баланса массы вещества для каждой из ячеек с учетом обратных (рециркуляционных) потоков между ними имеют вид:

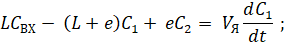
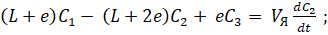
... (1).

.. .

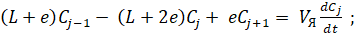
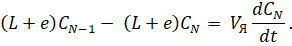
Соответствующие начальные условия для системы уравнения (1) имеют вид:

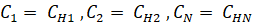
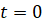
при (2).

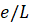
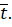
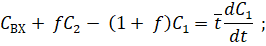
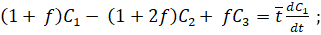
Соотнощение называется долей обратного потока и обозначается как. Отношениеопределяет среднее время пребывания потока в ячейке С учетом используемых допущений системы уравнений (1) и (2) запищем в виде:

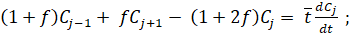
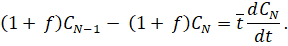
... (3).

.. .

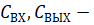
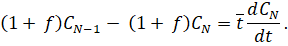
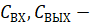
Принимаемиз таблицы № 1. Входными параметрами являются: масса гранул ПНД, масса добавляемого красителя (кг), охлаждающая жидкость (тосол) (л/мин), воздух (кг/см²), дробленка (кг), технологические добавки (кг). Выходными параметрами являются: изделия (шт/кг), облой (кг), отработанный воздух (кг/см²), охлаждающая жидкость (л/мин). Система уравнений (3) представляет собой математическое описание технологического процесса изготовления канистры из ПНД.

• 1. Graf Rudolf F. Modern dictionary of electronics. Boston: Newnes, 1999, 882 р. ISBN 978−0-75−69 866−5.
• 2. Meguid S. A. Integrated computer-aided design of mechanical systems. — London: Elsevier Applied Science, 1987, Р. 6 — 7 — ISBN 978−1-851−66 021−6.
• 3. Середкин А. Н., Виноградова Г. Л., Филиппенко В. О. Модель и методика параметризации при автоматизизированном проектировании изделий со сложной формой. // Инженерный вестник Дона, 2014, № 3 URL: ivdon.ru/ru/magazine/archive/n3y2014/2532.
• 4. Анисимов И. В. Математическое моделирование и оптимизация ректификационных установок / И. В. Анисимов, Бодров В. И., Покровский В. Б. М.: Химия, 1975. 216 с.
• 5. Ахназарова C.JI. Методы оптимизации эксперимента в химической технологии: учеб. пособие для хим. технол. спец. вузов / В. В. Кафаров. 2-е изд. М.: Высш. шк., 1985, 327 с.
• 6. Луценко В. А. Математическое моделирование химико-технологических процессов на аналоговых вычислительных машинах: Лабораторно-практические работы: Учеб. пособ. для вузов / М.: Химия, 1975. 336 с.
• 7. Демиденко Н. Д. Моделирование и оптимизация тепло-массообменных процессов в химической технологии / СО АН СССР. М.: Наука, 1991. 240 с.
• 8. Гумеров A.M. Математическое моделирование химико-технологических процессов: учеб. пособ. для вузов / Н. Н. Валеев, А. М. Гумеров, В. М. Емельянов. М.: Колос, 2008. 159 с.
• 9. Громов Ю. Ю. Специальные разделы теории управления. Оптимальное управление динамическими системами / H.A. Земской, A.B. Лагутин, О. Г. Иванова, В. М. Тютюнник: Учеб.пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2004. 108 с.
• 10. Прейс В. В. Проектирование машин и аппаратов пищевых и перерабатывающих производств. Учебное пособие. Тула: Изд-во ТулГУ. 2005. 156 с.
• 11. Разработка САПР. В 10 кн. Кн. 1. Проблемы и принципы создания САПР: Практ. пособие / А. В. Петров, В. М. Черненький; Под ред. А. В. Петрова. — М.: Высш. шк., 1990. 143 с.
• 12. Асцатуров Ю. Г., В. В. Семенов, Ю. Б. Ханжонков Разработка оптико-электронного устройства для анализа загрязнённости моторного масла двигателя внутреннего сгорания дисперсными частицами // Инженерный вестник Дона, 2014, № 2 URL: ivdon.ru/ru/magazine/archive/n2y2014/2376.