Турбулентное течение. 
Турбулентное течение

1. Турбулентное течение жидкости в гладких трубах

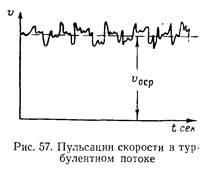
Для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений в процессе течения. Если с помощью особо чувствительного прибора-самописца измерить и записать пульсацию, например, скорости по времени, то получим картину, подобную показанной на рис. 57. Величина скорости беспорядочно колеблется около некоторого осредненного по времени значения _оср, которое в данном случае остается постоянным.

Траектории частиц, проходящих через данную неподвижную точку пространства, в разные моменты времени представляют собой кривые линии различной конфигурации несмотря на прямолинейность трубы. Характер линий тока в трубе в данный момент времени также отличается большим разнообразием (рис. 58). Таким образом, строго говоря, турбулентное течение является неустановившимся течением, так как величины скоростей и давлений, а также траектории частиц меняются по времени. Однако в расчетах его можно рассматривать как установившееся при условии, что осредненные по времени значения скоростей и давлений, а также величина полного расхода потока, не меняются с течением времени. Такое течение жидкости встречается на практике достаточно часто.

Ввиду того, что при турбулентном течении отсутствует слоистость потока и происходит перемешивание жидкости, закон трения Ньютона в этом случае неприменим. Вследствие перемешивания жидкости и непрерывного переноса количеств движения в поперечном направлении касательное напряжение на стенке трубы в турбулентном потоке значительно больше, чем в ламинарном при тех же значениях числа Rе и динамического давления, подсчитанных по средней скорости потока.

Распределение скоростей (осредненных по времени) в поперечном сечении турбулентного потока существенно отличается от того, которое характерно для ламинарного течения.

Если сравнить кривые распределения скоростей в одной и той же трубе и при одном и том же расходе (одинаковой средней скорости), но при ламинарном и турбулентном режимах, то будет заметно существенное различие в указанных кривых. Распределение скоростей при турбулентном режиме более равномерно, а нарастание скорости у стенки — более крутое, чем при ламинарном режиме, для которого, как уже известно, характерен параболический закон скоростей.

В связи с этим коэффициент, учитывающий неравномерность распределения скоростей в уравнении Бернулли, при турбулентном режиме значительно меньше, нежели при ламинарном. В отличие от ламинарного режима, где он не зависит от числа Rе, здесь коэффициент является функцией числа Rе, уменьшаясь с увеличением последнего от 1,13 при Rе=Rе_кр, до 1,025 при Rе=3 * 10⁶. Как видно из графика, приведенного на рис. 60, кривая по Rе асимптотически приближается к единице. В большинстве случаев при турбулентном течении можно принимать =1.

Потери энергии при турбулентном течении жидкости в трубах постоянного сечения (т.е. потери напора на трение) также получаются иными, нежели при ламинарном. В турбулентном потоке потери напора на трение значительно больше, чем в ламинарном при тех же размерах, расходе и вязкости.

Это увеличение потерь вызывается вихреобразованиями, перемешиванием и искривлением траекторий. Если при ламинарном режиме течения потеря напора на трение возрастает пропорционально скорости (а также расходу) в первой степени, то при переходе к турбулентному режиму заметен некоторый скачок сопротивления и затем более крутое нарастание величины h_тр по кривой, близкой к параболе второй степени.

Ввиду сложности турбулентного режима течения и трудностей его аналитического исследования, до сих пор мы еще не имеем достаточно строгой и точной теории этого течения. Существуют так называемые полуэмпирические, приближенные теории турбулентности Прандтля, Кармана и др.

В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются чисто экспериментальными данными, систематизированными на основе гидродинамической теории подобия.

Основной расчетной формулой для турбулентного течения в круглых трубах является уже приводившаяся выше универсальная формула, которая непосредственно вытекает из соображений подобия и имеет следующий вид:

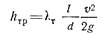
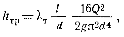
Эта основная формула применима как при турбулентном, так и при ламинарном режимах; различие заключается в значениях коэффициента .

Так как при турбулентном течении потеря напора на трение приблизительно пропорциональна квадрату скорости (и квадрату расхода), то коэффициент потерь на трение в формуле в первом приближении для данной трубы можно считать величиной постоянной.

Однако из закона гидродинамического подобия следует, что коэффициент _т, так же как и _л, должен являться функцией основного критерия подобия, т. е. числа Рейнольдса, включающего в себя скорость, диаметр и вязкость, т. е.

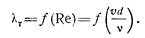
Существует ряд эмпирических и полуэмпирических формул, выражающих эту функцию для турбулентного течения в гладких трубах; одной из наиболее удобных и употребительных является формула П. К. Конакова, имеющая следующий вид.

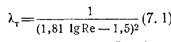
и применима от Rе=Rе_кр до Re, равного нескольким миллионам.

При числах Рейнсльдса 2300⁵ можно пользоваться также старой формулой Блазиуса.

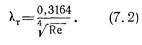
Отсюда видно, что с увеличением числа Re коэффициент _т уменьшается, однако это уменьшение гораздо менее значительно, чем при ламинарном режиме.

Это различие в законах изменения коэффициента связано с тем, что непосредственное влияние вязкости жидкости на сопротивление в турбулентном потоке гораздо меньше, чем в ламинарном. Если в последнем потери напора на трение прямо пропорциональны вязкости, то в турбулентном потоке эти потери пропорциональны вязкости в степени ¼. Дело в том, что основную роль в турбулентном потоке играют перемешивание и перенос количеств движения.

Приведенные формулы для определения коэффициента потерь на трение справедливы для так называемых технически гладких труб, т. е. для таких, шероховатость которых столь мала, что на сопротивление практически не влияет. К числу технически гладких труб можно без большой погрешности отнести цельнотянутые трубы из цветных металлов (включая и алюминиевые сплавы), а также бесшовные стальные трубы тщательного изготовления. Таким образом, трубы, употребляемые на самолетах в качестве топливопроводов и для гидропередач (гидросистем), в обычных условиях можно считать гладкими и для их расчета пользоваться приведенными формулами. Водопроводные стальные и чугунные трубы уже нельзя считать гладкими, так как они обычно дают повышенное сопротивление.

Вопрос о сопротивлении шероховатых труб будет рассмотрен ниже (см. § 30).

Как следует из теории подобия, при турбулентном течении жидкости в трубах непосредственно на стенке трубы обычно имеется так называемый ламинарный слой. Это весьма тонкий слой жидкости, движение в котором является наиболее замедленным, слоистым и без перемешивания, т. е. ламинарным.

В пределах этого ламинарного сдоя скорость круто нарастает от нулевого значения на стенке до некоторой конечной величины на границе слоя. Толщина ламинарного слоя _л крайне невелика, причем оказывается, что число Re, подсчитанное по параметрам слоя есть величина постоянная, т. е.

Эта величина имеет универсальное постоянное значение подобно тому, как постоянно критическое число Re для течения в трубах. Поэтому, при увеличении скорости потока, а следовательно, и числа Re, растет также скорость, а толщина ламинарного слоя уменьшается. При больших числах Re ламинарный слой практически исчезает.

Из описания турбулентного течения следует, что истинную местную скорость в турбулентном потоке в данный момент времени следует рассматривать как сумму осредненной по времени скорости и некоторого положительного или отрицательного приращения, называемого пульсационной скоростью. Условимся обозначать величины, осредненные по времени, чертой вверху, а пульсационные скорости — штрихом.

Тогда для составляющей местной скорости вдоль оси трубы (ось х) можно записать.

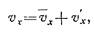
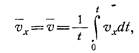
t — отрезок времени, за который осредняется скорость.

Так как осредненный поток вдоль осей у и z в прямой трубе постоянного сечения отсутствует, то соответствующие составляющие скорости равны нулю. Очевидно, что осредненное значение пульсационных скоростей, определенное таким же способом за достаточный промежуток времени, равно нулю. т. е.

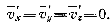
Осредненное значение касательного напряжения за промежуток времени t:

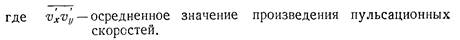
Будем иметь:

Полученное выражение именуется формулой Л. Прандтля и является законом турбулентного трения, который используется в теории турбулентных течений так же, как закон трения Ньютона в теории ламинарных течений.

Величина l, носящая название «путь смешения», представляет собой длину, пропорциональную осредненному по времени перемещению частиц в поперечном направлении. Путь смешения можно рассматривать как понятие, которое в некоторой степени подобно понятию длины свободного пробега молекул в кинетической теории газов (следует иметь в виду, что в процессе турбулентного перемешивания происходит перемещение не отдельных молекул, а частиц жидкости, состоящих из большого числа молекул).

Очевидно, что в разных точках поперечного сечения трубы величина l имеет разные значения. На стенке трубы и в пределах ламинарного слоя, где поперечные перемещения частиц отсутствуют, величина l равна нулю.

По мере удаления от стенки (точнее — от границы ламинарного слоя) увеличивается возможность поперечных перемещений частиц, турбулентное перемешивание делается все более интенсивным и путь смешения l растет.

Л. Прандтль предложил считать, что l растет по линейному закону в зависимости от расстояния до стенки у, т. е.

гдекоэффициент пропорциональности, имеющий, как показывают опыты, одинаковое значение для всех случаев турбулентного течения (порядка 0,4) и называемый поэтому универсальной постоянной турбулентного потока.

Далее Прандтль, рассматривая течение вдоль бесконечной плоскости, положил касательное напряжение в турбулентном потоке постоянным и равным напряжению на стенке _о.

При этих допущениях из формулы получаем после интегрирования ;

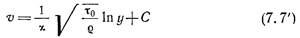
(знак осреднения у скорости здесь и в дальнейшем опускается).

Таким образом, закон распределения скоростей в турбулентном потоке по теории Прандтля получается логарифмическим.

Путем несложных преобразований формулу можно привести к следующему безразмерному виду:

Закон распределения скоростей в последней форме называется универсальным законом, так как опытные точки, полученные в разных трубах и при различных числа Re, ложатся на единую кривую. Еще более показательным является график зависимости.

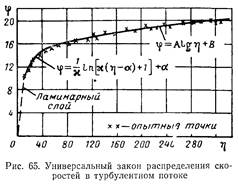
Теория Прандтля может быть уточнена путем учета вязкости ламинарного слоя.

Можно получить упрощенную форму закона распределения скоростей в турбулентном потоке с учетом ламинарного слоя и вязкости в виде.

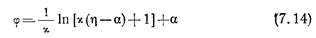
После несложных преобразований получим уточненный закон сопротивления в следующем виде:

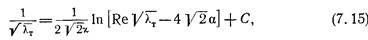
где.

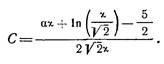
Таким образом, постоянные коэффициенты выражаются через две универсальные константы, определение которых из опытов =0,401−0,407 и =6,82−6,93.

Итак, учет вязкости и ламинарного слоя в теории Прандтля позволяет получить уточненные законы распределения скоростей и сопротивления, обеспечивает удовлетворение граничному условию закона распределения скоростей вблизи стенки и дает возможность выразить все постоянные коэффициенты через две универсальные константы и .

турбулентный жидкость труба Если для гладких труб коэффициент потерь на трение вполне определяется числом Re, то для шероховатых труб его значение зависит еще и от шероховатости внутренней поверхности трубы. При этом важен не абсолютный размер бугорков шероховатости k, а отношение этого размера к радиусу трубы, т. е. так называемая относительная шероховатость k/r_o. Одна и та же абсолютная шероховатость может совершенно не сказаться на сопротивлении трубы большого диаметра, но способна значительно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости: расстояния между бугорками, неравномерность по высоте и пр. Простейшим случаем будет тот, когда все бугорки шероховатости имеют один и тот же размер k и одинаковую форму, т. е. при так называемой равномерно распределенной зернистой шероховатости.

Таким образом, в случае равномерно распределенной зернистой шероховатости коэффициент _т:

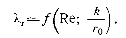
• 1) При ламинарном режиме шероховатость на сопротивление не влияет.
• 2) Критическое число Re от шероховатости практически не зависит.
• 3) В области турбулентного течения, но при небольших значениях Re и k/r₀, шероховатость на сопротивление не влияет. Однако при увеличении числа Re это влияние начинает сказываться.
• 4) При больших значениях числа Re и больших относительных шероховатостях коэффициент _т перестает зависеть от числа Re и делается постоянным для данной относительной шероховатости.

Можно отметить, следующие три области чисел Re и k/r_o, отличающиеся друг от друга характером изменения коэффициента _т.

Первая область-область малых Re и k/r_o, где коэффициент от шероховатости не зависит, а определяется лишь числом Re, как для гладких труб.

Вторая область, где коэффициент _т зависит одновременно от двух параметров: от числа Re и от относительной шероховатости, Третья область — область больших Re и k/r_o, где коэффициент _т не зависит от числа Re, а определяется лишь относительной шероховатостью. Эту область называют областью автомодельности или режимом квадратичного сопротивления, так как независимость коэффициента _т от числа Re означает, что потеря напора пропорциональна точно квадрату скорости.

Необходимо учесть также наличие ламинарного слоя. Как указывалось, при увеличении числа Re толщина ламинарного слоя уменьшается. Поэтому, когда мы имеем турбулентный поток в шероховатой трубе, то при малых числах Re толщина ламинарного слоя больше величины бугорков шероховатости, последние находятся внутри ламинарного слоя, обтекаются плавно (безотрывно) и на сопротивление не влияют. По мере увеличения числа Re толщина уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влиять на величину сопротивления. При больших числах Re толщина ламинарного слоя делается исчезающе малой, а бугорки шероховатости обтекаются турбулентным потоком со срывом и вихреобразовниями за каждым бугорком; этим и объясняется квадратичный закон сопротивления, имеющийся в данной области.

Для практических расчетов по определению сопротивления реальных шероховатых труб можно рекомендовать также следующую новую универсальную формулу А. Д. Альтшуля:

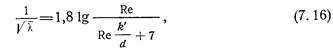
где d-диаметр трубы; k'-размер, пропорциональный абсолютной шероховатости.

Формула для вполне шероховатых труб, т. е. для режима квадратичного сопротивления (автомодельности).

Выше мы рассматривали турбулентное течение в трубах круглого сечения. Однако иногда приходится иметь дело с турбулентным течением в некруглых трубах, применяемых, например, в охлаждающих устройствах.

Рассмотрим расчет потерь на трение при турбулентном течении в трубе с поперечным сечением произвольной формы.

Суммарную силу трения, действующую на внешнюю поверхность потока, можно выразить следующим образом:

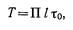
где П-периметр сечения;

При заданной площади сечения и данном расходе жидкости (а следовательно, и при заданной средней скорости) сила трения пропорциональна периметру сечения. Поэтому для уменьшения силы трения, а также потерь энергии на трение следует периметр сечения уменьшать. Наименьшим периметром при заданной площади обладает круглое сечение, которое поэтому является наивыгоднейшим с точки зрения получения минимальных потерь энергии (напора) на трение в трубе.

Для количественной оценки влияния формы сечения на потерю. напора вводится в расчет так называемый гидравлический радиус R_r, равный отношению площади сечения трубы к его периметру:

Гидравлический радиус может быть подсчитан для любого сечения. Например, для круглого сечения имеем.

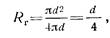
для прямоугольного сечения со сторонами, а и b:

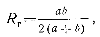
Для зазора размером, а из предыдущего получаем:

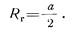
Подставив выражение геометрического диаметра d через гидравлический радиус в основную формулу для потери напора на трение, будем иметь:

Опыт подтверждает применимость формулы для труб с любой формулой поперечного сечения. Число Рейнольдса выражается через R_r, т. е.