Непараметрический регулятор нелинейных процессов

Значительная часть современных методов синтеза систем управления технологическими процессами базируется на линейных представлениях об объекте управления. Главной особенностью линейных процессов является допущение справедливости принципа суперпозиции. Однако, большинство существующих процессов линейными можно назвать лишь условно. Поэтому попытка получить глобальную модель нелинейного объекта практически обречена. В настоящее время целым рядом математических и физических школ развивается подход, основанный на неравновесной динамике, позволяющей все шире ставить вопрос об объекте управления как о «черном ящике». В представленной работе развивается именно такой подход. Приведенные результаты дают основания считать такой подход более рациональным, чем линейный.

Ключевые слова: мобильная модель, локальная модель, глобальная модель, расширенная матрица, аттрактор, бифуркация, бассейны, репеллеры, принцип суперпозиции, «черный ящик» .

Проблема и ее связь с научными и практическими задачами

История построения моделей динамических систем большей частью основана на линейной концепции, согласно которой принцип суперпозиции является главным. Отсюда и математический аппарат таких моделей: линейные дифференциальные и разностные уравнения с постоянными коэффициентами, частотные методы, передаточные функции, корреляционные модели. Такие допущения создают иллюзию, что по немногим данным траекторных измерений в расширенном пространстве состояний, включающем как выходные так и управляющие переменные, можно получить глобальную модель.

Построение глобальных молей объекта управления не всегда оправдано. Эта задача сама по себе тривиальна, если речь идет о линейных системах с постоянными параметрами. Однако большинство систем нелинейны. Для облегчения (но не достижения адекватности) как правило, производят линеаризацию модели и далее производят подмену объекта его линейной идеализацией. Однако при этом теряется информация об аттракторе, бифуркациях и других свойствах реального нелинейного объекта. Приходится «аппроксимировать» этот объект моделями линейных дифференциальных уравнений на отдельных областях состояний (TS-модели). При этом задача скорее усложняется, так как необходимо определить хотя бы условно (размыто) границы этих областей.

Авторам, знакомым с реальными нелинейными объектами и процессами, хорошо известно, что так называемые нелинейные характеристики объектов получить с достоверностью практически очень сложно, а иногда просто невозможно. Происходит это по следующим причинам. Для получения нелинейных характеристик технологических процессов необходимо остановить нормальный процесс эксплуатации объекта, что не всегда допустимо. Особенно это касается объектов, встроенных в технологические цепочки и обратные технологические связи. Например, доменный, процесс дробления или измельчения и много других. Даже, если это допустимо, эти характеристики могут эволюционировать даже в процессе измерений. Например, в процессе измерения характеристик дробления состав руды изменился.

Методы получения моделей, основанные на подаче стандартных воздействий, интегралов типа Дюамеля, вообще к нелинейным нестационарным системам неприменимы.

Методы, основанные на корреляционных функциях (уравнение Винера) также применимы только к линейным стационарным объектам. Варианты моделей Винера-Гаммерштейна, основанные на точном знании и стационарности нелинейных характеристик, требуют строгого обоснования. Кроме того, для получения корреляционных функций необходимо использование большого числа данных с объекта управления. Однако, в этом случае надо считаться с известным эффектом «устаревания данных». Этот эффект, возможно, несущественен, когда речь идет о линейных стационарных системах.

Использование частотных методов также неприменимо к нелинейным и, тем более нестационарным объектам, так как для них не справедлив принцип суперпозиции.

При попытке получить модель нелинейной системы в виде нелинейных дифференциальных уравнений возникает проблема выбора класса функций, аппроксимирующих вектор-функцию правых частей уравнений (скоростей фазовых траекторий). При этом часто выбирают функции из класса полиномов или тригонометрических функций. Этот математический аппарат удобен тем, что допускает аналитическое дифференцирование, интегрирование, а также все основные арифметические операции (в случае деления приближенно). Кроме того, работы Веерштрасса, Чебышева, Фурье и других ученых дают указания по оценке результатов применения этих функций. Однако, построить глобальную модель нелинейного нестационарного динамического объекта с помощью этого аппарата невозможно. Ведь параметры правых частей уравнений можно получить только в той области состояний объект и в то время, когда они определены.

В то же время при реализации управления объектами важно знать самые последние характеристики и причем на небольшом, предыдущем текущему управлению, отрезке времени. Знание модели в отдаленном прошлом и отдаленном будущем может представлять лишь исторический интерес. Очевидно, популярная (до сих пор серьезно не реализованная) идея дуального управления Фельдбаума А. А. в данном контексте является наиболее обоснованной. Что приводит к мысли о преимуществах локальных моделей, которые сменяются вдоль траектории движения объекта. Такие модели автором данной работы предлагается называть мобильными моделями.

Анализ исследования и публикаций

При дальнейшей разработке методики получения математических моделей (идущей, по-видимому, из идей сплайн-интерполяции) в качестве исходного материала стали применять на отдельных областях состояний объекта линейные дифференциальные уравнения. На основе работ [1−2 ] производится сращивание линейных дифференциальных моделей на отдельных областях пространства состояний (так называемые TS-модели). Относительно универсальных аппроксиматоров такого типа нейросетей можно сказать: «В общем случае результат зависит от очень многих параметров, начиная с входных и выходных данных, способа их нормирования, количества скрытых слоев и количества нейронов в этих слоях, уровня обучения, количества эпох обучения и многих, многих других.» [3 ].

Кроме того, возникают проблемы определения границ применимости той или иной дифференциальной модели. Более того, нелинейные процессы-оригиналы, а не их модели, могут иметь аттракторы, которые определить с помощью кусочно-линейных моделей невозможно. Это касается также возможных точек бифуркации, а также катастроф (хотя бы в виде быстрых фазовых переходов). Все это связано также с чувствительностью, которая может быть существенной и объясняться непредвиденными изменениями объемов областей начальных условий вдоль траектории движения. Возможно наличие бассейнов и репеллеров, на границах которых возможны специфические явления (например, в точках максимума производительности мельницы уравнения модели в приращениях содержат точку бифуркации.

В нелинейных системах могут возникать внутренние детерминированные хаотические процессы, что в линейных моделях просто невозможно.

Можно было бы далее анализировать указанные проблемы. Достаточно лишь заметить, что в настоящее время уже прочно входит в сознание многих исследователей физических, технологических, общественных, биологических и других явлений «нелинейное мышление» .

Что касается процессов дезинтеграции горных пород, следует особо отметить работы [4−5 ], в которых, с точки зрения автора настоящей статьи, впервые для анализа процессов дезинтеграции используются современные методы нелинейной динамики.

Для утилитарных локальных задач управления (а их большинство) не имеют значение глобальные свойства объекта за пределами локальной области движения (управления).

Глобальная модель имеет смысл, если она пригодна (в случае необходимости) на больших горизонтах прогноза. В линейных стационарных случаях это возможно. Однако, пока мы строим глобальную модель нелинейного нестационарного объекта, он изменяется и не соответствует модели.

Часто при решении задач конструирования регуляторов необходимо реализовать траектории движения в ограниченном объеме («трубке») фазового пространства. Поэтому усилия по созданию глобальной модели (даже адекватной, но, разумеется, сложной) часто совершенно неоправданны.

Из законов кибернетики следует, что разнообразие регулятора должно быть не менее разнообразия объекта. На этом основании регулятор нелинейных процессов должен быть нелинейным.

Нахождение параметров модели в классическом смысле в виде чисел (чем заполнены все работы до настоящего времени) не является целью при решении задачи управления. Ведь задача управления как раз формулируется как задача определения собственно управляющего воздействия, а параметры регулятора в виде конкретных чисел это промежуточный этап. Кроме того, традиционный классический подход определения параметров регуляторов и связывание их с физическими параметрами объекта управления требует осмысления. Ведь параметры реального объекта (например, постоянные времени электромеханического оборудования на прокатном стане) — это физические параметры физического объекта, а параметры регулятора, даже численно равные параметрам объекта, это всего лишь числа в памяти управляющего устройства. Параметры объекта изменяются независимо от чисел в ячейках памяти. Отсюда возникает, строго говоря, неправомерность сокращения полюсов и нулей передаточных функций.

В последние годы развивается методика создания дуальных непараметрических моделей объектов управления. Например, в работе [6] дан анализ такого подхода. Однако во всех работах такого направления сохраняется тенденция поставить в качестве первоочередной задачи определение параметров модели объекта, несмотря на указание в заголовках статей о синтезе «непараметрических» моделей.

Постановка задачи. Продемонстрировать на численных примерах возможность синтеза регулятора нестационарного нелинейного объекта управления как в устойчивом так и неустойчивом состоянии без необходимости измерения параметров, определения точной структуры, настройки регулятора на основе локальной модели и показать преимущества такого подхода.

В работах [7−9] приведена методика синтеза регулятора на основе матричной локальной модели, в основу которой положен известный дуальный подход, предложенный А. А. Фельдбаумом. В данной работе показан еще один прием синтеза такого регулятора. Этот прием проще использованного ранее. Что особенно важно, он позволяет автоматизировать получение основных результатов с помощью современных символьных процессоров, встроенных в различные приложения. В данном случае был использован символьный процессор приложения MATHCAD. Необходимо подчеркнуть, что из-за ограниченного объема статьи доказательство метода отложено до дальнейших публикаций автора.

Суть метода в следующем. На вход объекта управления подаются управляющие воздействия. в ходе нормальной его эксплуатации. В результате заполняется расширенная матрица вида.

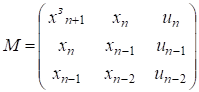
(1).

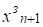
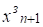
гдезначение выходной величины на (n+1) «будущем» заданном интервале дискретности, это может быть заданное желаемое значение; - значения выходной величины на k-м интервале (k n+1), которые были ранее реализованы, измерены; u_n-1, u_n-2 — значения управления на соответствующих прошедших интервалах, измерены и значит известны; u_n, — значение управления на n-м интервале (на котором осуществляется новое, рассчитанное) управление, обеспечивающее на следующем интервале заданное значение выхода.

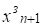
Таким образом, задача регулятора состоит по заданному значению определить соответствующее управление u_n. Для решения этой задачи предлагается найти неизвестное управление, алгоритм определения которого предложено в виде выражения.

det (M)=0. (2).

Откуда.

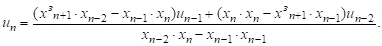
(3).

управление детерминированный нелинейный регулятор Очевидной особенностью такого регулятора является отсутствие коэффициентов, которые надо определять, а затем оптимизировать. Кроме того, пока речь не шла об уравнении модели управляемого объекта, как это до сих пор принято во всех публикациях. Однако очевидно, что матрица (1) и соответствующее уравнение регулятора содержат полную первичную (самую достоверную) информацию об объекте. Предложено называть, по аналогии с объектным программированием, моделью объекта управления матрицу (1) и алгоритм обработки этой матрицы (2). Результатом является управление (3). Такая модель, очевидно, изменяется вдоль траектории движения объекта и потому может называться мобильной. Для начала работы достаточно подать три обучающих допустимых управляющих воздействия, затем после определения первого рабочего управления u_n и далее матрица пополняется «свежими» данными и позволяет при заданном выходе x_n+1 определять очередное рабочее управляющее воздействие. Очевидно, что если не измеряемые непосредственно параметры объекта будут изменяться, то это неизбежно скажется на содержимом матрицы (1) и будет получено соответствующее управление (3).

Технологические механизмы дезинтеграции твердых материалов являются нелинейными. Поэтому для управления ими необходимо использовать нелинейные регуляторы в соответствии с упомянутыми законами кибернетики. Их нелинейные характеристики можно измерять, но только в статических режимах. Такая информация иногда создает иллюзию точности модели так как даже во время эксперимента характеристики могут изменяться. Поэтому надо стремиться создавать регуляторы, способные управлять объектами типа «черного ящика». Очевидно, что для регулятора (3) объект представляет собой «черный ящик», о котором известны лишь входные и выходные данные. Поэтому для такого регулятора в некотором смысле не имеет значение структура и параметры «черного ящика». Правда, что касается структуры, характерных режимов работы объекта, а также сигнатуры его ляпуновских показателей, более детальный ответ на этот вопрос, ввиду ограниченного объема данной работы, автор планирует привести в последующих публикациях.

Признаком высокого качества работы регулятора является его способность сохранять работоспособность при входе объекта в состояние неустойчивости. Ниже будет приведен пример численного испытания нелинейного объекта управления в дискретном пространстве. При этом корень его характеристического полинома превышает единицу (объект неустойчив). Задание изменяется по достаточно сложному закону. Как известно, при изменении параметров и вида задания ПИД-регулятор требует пересчета коэффициентов или настройки иногда по достаточно сложным алгоритмам, а в ряде работ с привлечением нейротехнологий. Нейротехнологии — это безусловно шаг в сторону нелинейного мышления и позволяет решать целый ряд задач. Однако, применение этих технологий для настройки двух-трех коэффициентов ПИД-регулятора представляется нерационалным.

В качестве объекта управления было взято неизвестное регулятору уравнение.

(4).

где a (n)=800sin (3ndt); dt=0.0005 — интервал дискретности; n — номер интервала дискретности.

Очевидно, корень уравнения (4) равен rut (n)=1+a (n)dt.

Далее на рис. 1 приведены графики изменения задания (x task), выхода x_n (x real) и корня rut (n).

При рассмотрении графиков необходимо учесть особенности дискретных систем. Известно, что результат управления должен отставать от задания минимум на один интервал. Это соответствует условиям физической реализуемости. Поэтому необходимо сравнивать заданное значение на n-м интервале с его реализацией на следующем (n+1)-м интервале. Если графики соответственно сдвинуть, то они практически совпадут. Средняя ошибка регулирования за один интервалы вычислялась путем сравнения заданного значения выхода и его реализации на следующем интервале, т. е., с учетом условия физической реализуемости.

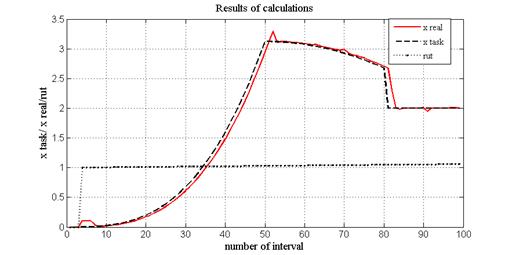
Рис. 1. Результаты вычислений.

Эта средняя на один интервал ошибка составила всего 1,29%. Начиная примерно с интервала номер 40, корень становится больше единицы. Объект становится неустойчивым. Среднее значение корня на 50 последующих интервалах составляет примерно 1.05, что соответствует темпу роста выхода объекта в автономном (без управления) режиме1.05⁵⁰= 11.4674. Однако, регулятор успешно справляется с задачей. Более детальные исследования показали, что даже при значении корня до 1.15, что соответствует темпу роста в автономном режиме1.15⁵⁰= 1.0837e+03, работа регулятора успешна.

Выводы. Приведенный в работе метод синтеза регулятора отличается полным отсутствием необходимости вычисления коэффициентов в соответствии с параметрами объекта управления и дальнейшей настройкой. Регулятор достаточно хорошо справляется с управлением неустойчивым объектом. Дальнейшая работа будет направлена на более глубокое обоснование применения рассмотренного класса регуляторов для регулирования многосвязных систем.

• 1. Tanaka K., Sugeno M. Stability analysis and design of fuzzy control systems // IEEE Trans. Fuzzy Syst. — 1992. — V. 45. — № 2. — P. 135−156.
• 2. Tanaka K., Wang H.O. Fuzzy control systems design and analysis: a linear matrix inequality approach. — N.Y.: Wiley, 2001.
• 3. Metatrader 5 — индикаторы. Третье поколение нейросетей: «глубокие нейросети» 27 ноября 2014, 10:37 2014, 10:3. Интернет-ресурс:https://www.mql5.com/ru/articles/1103
• 4. Герасина А.В. Структурно-параметрическая идентификация процессов дробления и измельчения руд: монография / А. В. Герасина, В. И. Корниенко. -Д.: Национальный горный университет, 2013. — 101 с.
• 5. Корнієнко В.І. Автоматизація оптимального керування процесами дроблення і здрібнювання руд: монографія / В.І. Корнієнко. — Д.: Національний гірничий університет, 2013. — 193 с.
• 6. Медведев А.В. О теории непараметрческих систем управления. Вестник Томского Государственного университета. Управление, Вычислительная Техника И Информатика, Выпуск № 1 (22) / 2013. С. 6−19. Научная библиотека КиберЛенинка. Интернет-ресурс: http://cyberleninka.ru/article/n/o-teorii-neparametricheskih-sistem-upravleniya.
• 7. Жосан А.А. Розробка алгоритмів дуального управління відцентровим дезінтегратором руд. Автореф. дис. на здобуття наукового ступеня кандидата технічних наук, КТУ, 1998 р. — 17 с. Спеціальність 05.13.07 — Автоматизація технологічних процесів.
• 8. Жосан А.А. Концепція моделі динамічного об'єкта керування як потоку вхідних і вихідних даних. Вісник Криворізького технічного університету. випуск 22, Кривий Ріг, 2008 (жовтень), С. 154−157.
• 9. Anatoliy Zhosan, Sergey Lipanchikov. Numerical modeling of disintegration process dual control. Metallurgical and Mining Industry, 2015, No. 3, p. p 74−77.