Структура атома в 5D

В пятимерном пространстве можно построить не только теорию поля, объединяющую электромагнитное и гравитационное взаимодействия [7−11], но и теорию атома и атомного ядра [16−18].

Можно заметить, что периодический закон в оригинальной формулировке Менделеева является локальным, так как связывает свойства простых веществ с их атомным весом, который в то время, когда был сформулирован закон, определялся путем взвешивания в гравитационном поле земли. Такое соотнесение свойств веществ с их гравитационными свойствами представляется разумным. Для ответа на вопрос о фундаментальных причинах, обуславливающих наличие закона периодичности в природе, рассмотрим общую модель атомных ядер и атомов вещества [16−18]. В этой модели свойства вещества определяются параметрами метрического тензора в 5-мерном пространстве, которые зависят от комбинации заряда и гравитационных свойств центрального ядра в виде [11].

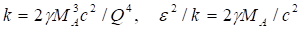
(20).

Здесь — гравитационная постоянная, скорость света и заряд ядра соответственно. Относительно природы заряда будет предполагать, что исходный заряд является электрическим. В случае протона и электрона параметры метрического тензора представлены в таблице 1.

Отметим, что максимальный масштаб в случае электрона превосходит размер наблюдаемой Вселенной, тогда как для протонов этот масштаб составляет около 100 световых лет. Минимальный же масштаб соответствует классическому радиусу заряженной частицы, который в случае протона и электрона соизмерим с масштабом слабых и ядерных взаимодействий.

Таблица 1. Параметры метрического тензора, вычисленные для электрона и протона.

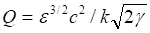
Легко видеть, что второй параметр (20) непосредственно входит в оригинальную формулу периодического закона Менделеева. Комбинируя параметры, находим заряд ядра в виде. Следовательно, периодический закон в современной его формулировке также можно выразить через параметры метрического тензора.

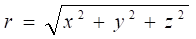
Метрический тензор можно разложить в ряд вблизи массивного центра гравитации в 5-мерном пространстве по степеням безразмерного расстояния до источника,, здесь. Рассмотрим вид метрического тензора, возникающего при удержании первых трех членов разложения для случая метрики в поле центральных сил с гравитационным потенциалом в форме Ньютона. Такой выбор метрики представляется оправданным, прежде всего, потому, что для указанного потенциала выполняется принцип суперпозиции. Положим, в этих обозначениях имеем для квадрата интервала в 4-мерном пространстве:

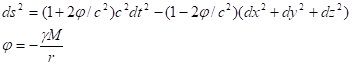
(21).

Полагая, что, приходим к выражению интервала в зависимости от параметров метрики в 5-мерном пространстве:

(22).

Далее заметим, что в этом случае метрический тензор в четырехмерном пространстве является диагональным с компонентами.

(23).

Зададим векторный потенциал источника, связанного с центром гравитации в виде.

(24).

Здесь — некоторый вектор в трехмерном пространстве, который определим ниже. Отсюда находим скалярный и векторный потенциал электромагнитного поля.

Для описания движения материи с учетом ее волновых свойств, предположим, что стандартное уравнение Гамильтона-Якоби в релятивистской механике и уравнение типа Клейна-Гордона в квантовой механике возникают как следствие выполнения волнового уравнения в 5-мерном пространстве [11]. Это уравнение в общем случае можно записать в виде:

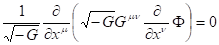
(26).

Здесь — волновая функция, описывающая, согласно (26), скалярное поле в пятимерном пространстве, — контравариантный метрический тензор,.

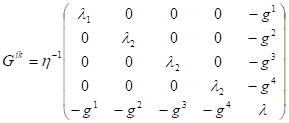
(27).

.

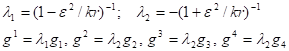
Далее заметим, что в исследуемой метрике, зависящей только от радиальной координаты, выполняется следующее соотношение.

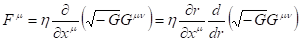
(28).

С учетом выражений (27) и (28) запишем волновое уравнение (26) в виде.

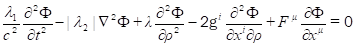
(29).

Отметим, что последнее слагаемое в уравнении (29) имеет порядок. Следовательно, это слагаемое можно отбросить в задачах, характерный масштаб которых значительно меньше, чем максимальный масштаб из таблицы 1. Уравнение (29) примечательно тем, что оно не содержит каких-либо параметров, характеризующих скалярное поле. Поле приобретает массу и заряд, не только электрический, но и сильный, в процессе взаимодействия с центральным телом, что обусловлено только метрикой 5-мерного пространства [11, 16−18].

Рассмотрим задачу о движении материи вокруг заряженного центра гравитации, обладающего электрическим и сильным зарядом, например, вокруг протона. В процессе решения этой задачи необходимо определить инерционную массу материи и энергию связи. Поскольку уравнение (29) является линейным и однородным, такую задачу можно решить в общем случае.

Введем полярную систему координат с осью z направленной вдоль векторного потенциала (24), положим в уравнении (29).

(30).

Разделяя переменные, находим, что радиальное распределение материи описывается следующим уравнением (здесь отброшено, в силу его малости, последнее слагаемое в уравнении (29)):

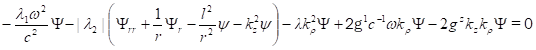
(31).

Рассмотрим решения уравнение (31) в том случае, когда можно пренебречь влиянием гравитации, т. е., но. При этих условиях уравнение (31) приводится к виду.

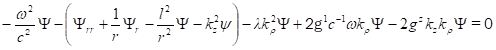
(32).

В общем случае решение уравнения (32) можно представить в форме степенного ряда.

(33).

Здесь обозначено. Подставляя выражение (33) в уравнение (32), находим.

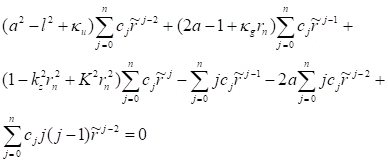
(34).

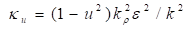
. Отсюда, приравнивая коэффициенты при одинаковых степенях, получим уравнения, связывающие параметры модели в случае возбужденных состояний.

(35).

Второе уравнение (35) выполняется лишь для таких значений показателя степени, для которых справедливо неравенство. Отсюда находим уравнение для определения уровней энергии.

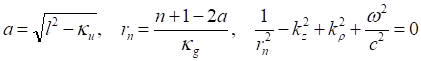
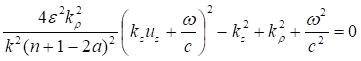
(36).

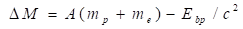
Уравнение (36) было использовано для моделирования энергии связи нуклонов в ядрах для всей совокупности известных нуклидов [16−18]. Отметим, что в модели [16−18] ядро состоит из «чистых» протонов, взаимодействующих со скалярным полем. Часть «чистых» протонов экранируется, образуя N нейтронов, в результате возникает атом, состоящий из электронной оболочки и ядра с электрическим зарядом eZ, числом нуклонов и массой, где — энергия связи нуклонов в ядре, вычисляемая по общему числу нуклонов, обладающих суммарной массой электрона и протона.

Такой способ выражения энергии связи не является существенным, поэтому можно ограничиться и стандартным выражением превышения массы в атомных единицах. Поскольку в этой задаче фигурирует два типа зарядов — скалярный и векторный, эффект экранирования проявляется не только в отношении скалярного заряда (что приводит к образованию нейтронов), но и в отношении векторного заряда, что приводит к образованию нуклонов.

Следует заметить, что исходная метрика в пятимерном пространстве определяется метрическим тензором, который зависит только от параметров центрального тела, т. е. от суммарного заряда и суммарной массы нуклонов. В зависимости от комбинации заряда и массы в ядре могут образоваться различные оболочки:

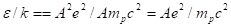
нуклонная оболочка, в которой все заряды экранированы, следовательно ;

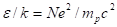
нейтронная оболочка, в которой ;

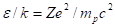
протонная оболочка, в которой .

Используя массу электрона и постоянную Планка, определим безразмерные параметры модели в виде.

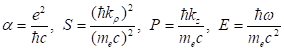
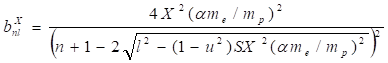
(37).

Здесь в случае нуклонной, нейтронной или протонной оболочки соответственно.

Разрешая уравнение (37) относительно энергии, находим.

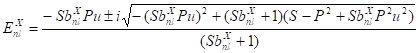
(38).

Заметим, что параметр энергии в уравнении (38) может принимать как вещественные, так и комплексные значения, которые соответствуют состояниям с конечным временем жизни. Учитывая, что для большинства нуклидов время распада является достаточно большой величиной, можно предположить, что мнимая часть числа в правой части уравнения (38) является малой величиной, что соответствует малой величине подкоренного выражения. Отсюда находим, что для этих состояний справедливо следующее соотношение между параметрами.

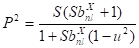
(39).

Подставляя выражение импульса (39) в уравнение (38), имеем.

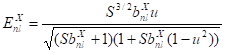
(40).

Отсюда находим зависимость энергии связи на один нуклон в основном состоянии.

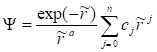
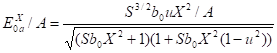
(41).

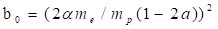
Здесь обозначено. Уравнение (41) позволяет описать зависимость энергии связи от числа нуклонов для всех нуклидов, а также энергию связи электронов в водородоподобном атоме [17−18]. Рассмотрим общее выражение энергии (38) в случае протонной оболочки и при условии полного экранирования магнитного заряда, т. е. положим. В результате находим.

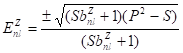
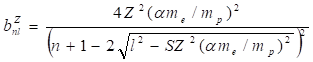
(42).

С другой стороны, в случае водородоподобного атома справедлива формула Зоммерфельда-Дирака для энергии релятивистского электрона [30].

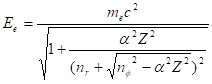
(43).

Сравнивая (42) и (43), находим, что для согласования этих формул следует положить.

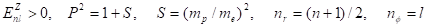
(44).

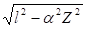
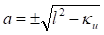
Отметим, что различия в знаках радикала связано с выбором знака параметра в выражении (35), где в общем случае следует полагать, что. В задачах моделирования структуры ядра мы выбрали положительный знак, тогда как в задачах моделирования атомных оболочек принято выбирать отрицательный знак. В последнем случае находим, что первое уравнение (42) совпадает с уравнением Зоммерфельда-Дирака (43):

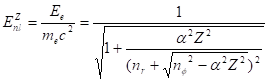
(45).

Таким образом, мы показали, что выражение (38) является универсальным. В области значений параметра это выражение описывает энергию связи нуклонов в ядрах элементов, тогда как при условии, оно описывает энергию релятивистских электронов в атомных оболочках.

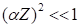
Первые члены разложения выражения (45) по степеням малого параметра, описывают энергетические уровни водородоподобного атома, включая атом водорода, в этом случае имеем [30].

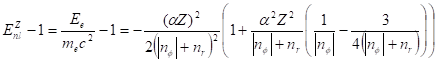
+… (46).

Выражение (46) описывает рентгеновские термы, квадратичная зависимость которых от заряда ядра была определена экспериментально Мозли, что послужило основой для создания квантовой механики и современной формы периодического закона.

Отметим, что общее выражение (38) содержит свободные параметры, которые в современной квантовой теории принимают частные значения (44). С учетом этих значений находим, что выражение (45) описывает не только энергию связанных состояний электрона в водородоподобном атоме (46), но и энергию свободного электрона, обусловленную его массой покоя. Исходное же уравнение теории (26) описывает движение скалярного поля, которое не обладает, ни зарядом, ни массой, ни спином. Следовательно, мы доказали, что масса покоя электрона, его заряд и спин обусловлены движение скалярного поля в пятимерном пространстве со специальной метрикой (27), зависящей от заряда и массы центрального ядра.

Этот результат указывает на новые возможности моделирования атомов и атомных ядер на основе общей теории относительности в многомерных пространствах.