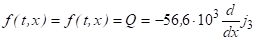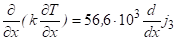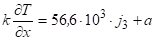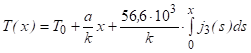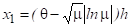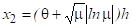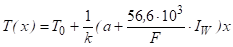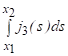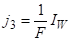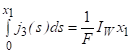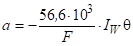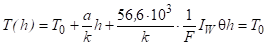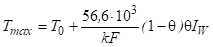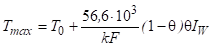Определение распределения температуры с помощью уравнения теплопроводности с распределенным источником тепла

Полученные выше в п. 2.2 оценки можно уточнить с учетом того, что в нашем случае внутренние источники тепла непостоянны:

.

тогда вместо (7) можно использовать уравнение:

. (11).

Интегрируя один раз (11) получим (12), где постоянная интегрирования.

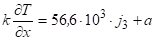
(12).

Поскольку ДС занимает небольшую часть КО, то можно предположить, что в ядре потока температура постоянна, т. е. при поддерживается постоянная температура. Интегрируя уравнение (12) еще раз от до произвольного, получим:

. (13).

Из [2] следует, что, при, где и, при, где. Поэтому при, получаем, а при: Так как, при, последний интеграл равен нулю, интеграл мал, а, то .

3) Поскольку отрезок мал, то предыдущие формулы можно продолжить на него по непрерывности.

Остается определить постоянную интегрирования исходя из краевого условия при. Постановка краевого условия при затруднено тем, что является межфазной границей, в которой происходят сложные процессы. Наиболее существенными из них являются эндотермическая реакция диссоциации молекул воды и джоулев нагрев раствора при прохождении тока, поэтому краевое условия при зависит от соотношения интенсивности этих процессов. В соответствии с эти рассмотрим разные варианты краевого условия при .

1) Предположим процессы диссоциации молекул воды и джоулев нагрев раствора уравновешивают друг — друга и температура при остается неизменной, поэтому. Тогда определяя из условия, получаем, следовательно, функция имеет вид, при. , при .

Таким образом, функция на отрезке линейно растет от до, а на отрезке линейно падает до .

2) Джоулев нагрев раствора преобладает, по крайней мере, вначале, над охлаждающим эффектом диссоциации молекул воды. Этот случай рассматривается ниже в п. 3.