Метод средних точек

Идея метода средних точек похожа на идею метода дрейфа — исследователь так же проводит прямую линию через две точки. Однако, в отличие от метода дрейфа, предполагается, что точки, через которые проводится линия, находятся в середине различных частей ряда данных.

Обратимся для начала к графической интерпретации метода. На рис. 5.13 представлена типичная ситуация, при которой некоторый показатель yt изменяется во времени. Из рисунка видно, что эта тенденция может быть описана линейным трендом, уравнение которого мы запишем так:

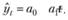(5.27).

Прогноз по линейной модели считается очень просто: вместо значения t достаточно подставить следующие номера наблюдений вплоть до требуемого горизонта прогнозирования: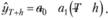

Как известно из начального курса геометрии, через точку на плоскости можно провести множество различных прямых линий; через две точки, лежащие на плоскости, — одну и только одну прямую линию, а вот если на плоскости лежит более двух точек, то провести через них прямую линию в общем случае нельзя. Исключением является ситуация, когда эти точки лежат на одной прямой, но такие ситуации в экономике не встречаются. Поэтому возникает.

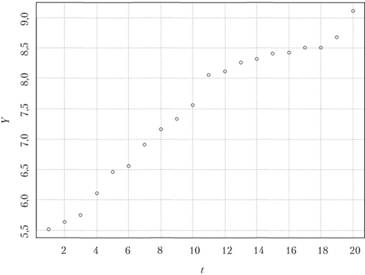
Рис. 5.13. Условный ряд данных с тенденцией к возрастанию.

задача — построить на плоскости рис. 5.13 прямую линию так, чтобы она наилучшим образом проходила через все точки или рядом с ними. Принципиально важным является ответ на вопрос: какой способ построения прямой линии мы будем признавать «наилучшим»? Существует много ответов на этот вопрос и, следовательно, много способов построения таких линейных моделей.

Но каким бы образом мы ни находили значения коэффициентов модели, при нанесении ее на график рис. 5.13 линия будет описывать исходные точки с некоторой ошибкой аппроксимации 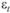. Математически эго будет выглядеть так:

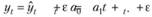(5.28).

Теперь задачу можно переформулировать следующим образом. Нам надо так найти коэффициенты прогнозной модели, чтобы ошибка аппроксимации была минимальной.

Метод средних точек относится к случаю, в котором исследователь может достаточно быстро и без привлечения специальных вычислительных технологий получить довольно сносную прогнозную модель, описывающую исходный ряд данных. Его суть заключается в следующем.

Поскольку для нанесения на плоскость прямой линии достаточно знать параметры двух точек, которые лежат на этой прямой, то прогнозисту необходимо каким-то образом найти эти две точки и их координаты. Очевидно, что в декартовой системе координат такие точки определяются координатами на осях этой плоскости. В рассматриваемом случае одной из координат будет выступать время t, а другой — значение показателя у. Пусть для определенности первая точка а имеет координаты (t1, y1), а вторая — b — координаты (t2, y2). Множество наблюдений динамического ряда у, является дискретным и лежит в пределах t = 1, 2, 3, …, Т.

Логично было бы предположить, что первая точка характеризует первую часть имеющегося множества наблюдений, а вторая — другую его часть. Поэтому разобьем имеющееся множество наблюдений на две части — первую, когда t =1, 2, 3, …, Т/2, и вторую — когда t=T/2+1, T/2+2, Т/2+3, …, Т. Хорошей статистической характеристикой множества случайных наблюдений является средняя арифметическая, поэтому разумнее всего рассматривать первую точку как среднюю арифметическую первой части множества, а вторую — как среднюю арифметическую второй части этого множества.

Найдем координаты точки а.

Координата этой точки, откладываемая на оси времени t, будет найдена как средняя арифметическая отсчетов времени t в промежутке от t = 1 до t = T/2: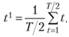

Если время отмечается через равные промежутки времени, то эту среднюю можно найти достаточно легко, поскольку мы имеем дело с арифметической прогрессией, сумма элементов которой, как известно, находится по формуле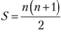

С учетом этого получим окончательно:

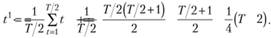(5.29).

Например, множество наблюдений состоит из 20 точек. Тогда координата первой точки, откладываемой по оси времени для первых десяти отсчетов времени, будет равна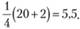

Вторая координата первой точки, которая откладывается по оси у, находится как средняя арифметическая первой части ряда данного показателя:

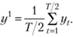(5.30).

Аналогично найдем координаты второй точки. Средняя арифметическая для второй части временного ряда 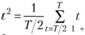также может быть легко найдена с помощью формулы для расчета суммы арифметической прогрессии:

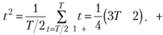(5.31).

Для рассмотренного примера с 20 наблюдениями средняя арифметическая второго участка наблюдений в промежутке от t = 11 до t = 20, будет равна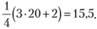

Координата этой точки на оси у, будет найдена как средняя арифметическая:

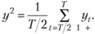(5.32).

Графически нахождение координат точек а и b можно представить следующим образом (рис. 5.14).

Вначале исследователь разбивает ряд данных t на две части (вертикальная линия на рис. 5.14) и находит среднюю величину в первой и во второй частях, что соответствует координатам, но оси абсцисс точек а и b. То же самое делается и с рядом данных у (горизонтальная линия на рис. 5.14). Так можно получить координаты средних точек.

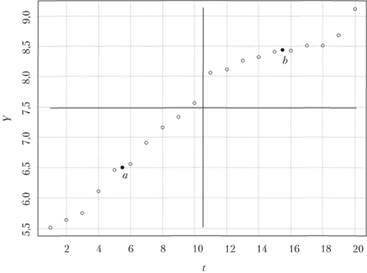
Рис. 5.14. Графическое представление нахождения координат точек а и b при нахождении коэффициентов прямой методом средних точек.

Поскольку мы намерены провести прямую линию через первую точку, что означает принадлежность точки прямой, то выполняется равенство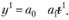

Точно так же выполняется равенство и для второй точки: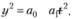

Объединяя эти два равенства, получим систему двух уравнений с двумя неизвестными а0 и ал, которая с учетом (5.29), (5.30), (5.31) и (5.32) будет записана так:

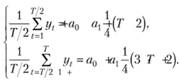(5.33).

Если от левой и правой частей второго уравнения данной системы отнять соответственно левые и правые части первого уравнения, то коэффициент а0 сократится, откуда легко найти значения коэффициента пропорциональности а1:

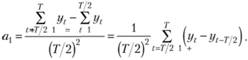(5.34).

Подставляя полученное значение в первое или второе уравнение системы (5.33), легко найти значения свободного коэффициента а0 и тем самым вычислить приближенные параметры линейного тренда. Для нашего условного примера итоговый линейный тренд пройдет через точки а и b так, как это показано на рис. 5.15.

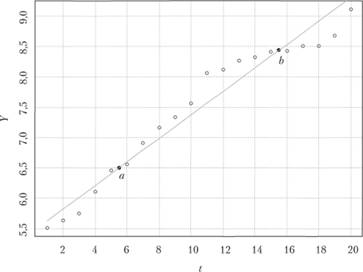
Рис. 5.15. Условный ряд данных и линейный тренд, коэффициенты которого были найдены методом средних точек.

Данный способ может быть распространен и на нелинейные тренды. Логика метода средних точек в этом случае будет такова. Все точки имеющегося ряда значений у, разбиваются равномерно на группы, количество которых будет равно числу п коэффициентов прогнозной модели аi, i = 1, 2, … п. Для каждой п-й группы находятся их средние арифметические. Подставляя эти средние в модель, можно получить последовательно столько равенств, сколько неизвестных коэффициентов у модели. Решая полученную систему, находят искомые значения параметров модели.

В случае, когда число наблюдений Т оказывается нечетным, а число коэффициентов четно (например, когда линейный тренд оценивается на 41 наблюдении), возникает проблема разбиения исходных рядов значений уt и tt на четное число частей, которые не будут равны друг другу по численности членов ряда. При этом можно предложить различное множество способов разбиения точек имеющегося ряда на неравные группы. В результате будет получено несколько моделей, отличающихся друг от друга как точностью аппроксимации, так и качеством прогнозных свойств.

Для целей прогнозирования необратимых процессов имеет смысл учитывать, что тенденции могут изменяться во времени. В этом случае можно поступить одним из следующих способов:

• 1. Разбить ряд данных на части, содержащие разное количество точек. Таким образом, для нахождения координат одной точки будет использоваться больше наблюдений, чем для другой, т. е. фактически какой-то части ряда будет придаваться больший вес.
• 2. Убрать из анализа ранние наблюдения и оставить только те наблюдения, в которых прослеживаются нужные для целей прогнозирования тенденции. По оставшемуся после отсечения ряду данных можно применить метод средних точек. Так из рассмотрения просто убирается часть устаревшей информации, которая может сильно исказить прогноз.

Оба эти способа, однако, требуют экспертного мнения относительно того, что оставлять и сколько точек включать в ту или иную часть, что не всегда легко сделать.

Кроме упомянутых недостатков, можно отметить, что метод средних точек пригоден только для очень простых приближенных расчетов. К тому же полученные оценки будут обладать не очень хорошими статистическими характеристиками: значения коэффициентов модели будут смещены и, возможно, неэффективны и несостоятельны.

Преимущества и недостатки простейших методов прогнозирования

Изучив простейшие методы прогнозирования социальноэкономических тенденций, попробуем обобщить их преимущества и недостатки.

К первому однозначному преимуществу всех рассмотренных методов можно отнести то, что в них используется минимум априорных предположений о процессах, протекающих в объекте исследования. Чем меньше предположений относительно поведения объекта исследования вводится, тем меньше возможностей для получения состояний, противоречащих введенным предположениям.

Второе неоспоримое преимущество упомянутых методов заключается в том, что они могут быть построены с минимальными затратами времени и труда. Первые три метода, рассмотренные нами в этом параграфе (метод средних величин, Naive и сезонный Naive), позволяют получать неплохие по точности краткосрочные прогнозы, однако из-за их простоты на практике эти методы используются нечасто, так как исследователю бывает чисто психологически сложно поверить, что такой простой метод может дать приличные прогнозные результаты. Последние два метода (метод дрейфа и метод средних) позволяют быстро построить прогноз по наиболее часто встречающимся на практике тенденциям — линейным.

К недостаткам методов можно отнести в первую очередь то, что в случае наличия тенденций в ряде данных первые три метода на среднесрочной перспективе будут давать неточные прогнозы. Главный недостаток метода дрейфа заключается в том, что он подразумевает построение лишь линейных трендов. Метод средних, в свою очередь, в случаях с построением более сложных моделей (через большее двух количество точек) требует решения систем, состоящих более чем из двух уравнений, что нивелирует его преимущество в простоте построения, проявляющееся лишь с линейными трендами.

Кроме того, для эффективного использования метода средних и метода дрейфа требуется экспертное мнение относительно того, какую часть ряда брать и как именно рассчитывать коэффициенты тренда. Стандартные алгоритмы построения моделей линейного тренда этими методами в случае со сложной динамикой показателя дают неточные прогнозы.