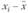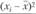Статистический анализ. 
Информационные системы маркетинга

Для анализа данных могут применяться разные методы. Статистические методы анализа данных предназначены для их уплотнения, выявления взаимосвязей и структур.

Статистические методы — методы анализа статистических данных. По своей природе они делятся на количественные и категориальные.

Количественные (метрические) данные являются непрерывными по своей структуре. Эти данные либо измерены с помощью интервальной шкалы (числовая шкала, количественно равные промежутки которой отображают равные промежутки между значениями измеряемых характеристик), либо с помощью шкалы отношений (кроме расстояния определен и порядок значений).

Категориальные (неметрические) данные — это качественные данные с ограниченным числом уникальных значений и категорий. Существует два вида категориальных данных: номинальные — используется для нумерации объектов и порядковые — данные, для которых существует естественный порядок категорий.

Статистические методы делятся на однои многомерные. Одномерные методы используются тогда, когда все элементы выборки оцениваются единым измерителем либо если этих измерителей несколько для каждого элемента, но каждая переменная анализируется при этом отдельно ото всех остальных.

3.4.3.1. Одномерные статистические методы

• Одномерные статистические методы (Univariate techniques) — методы статистического анализа данных в случаях, если существует единый измеритель для оценки каждого элемента выборки либо если эти измерителей несколько, но каждая переменная анализируется отдельно от всех остальных [12].

Одномерные методы (рис. 3.9) можно классифицировать на основе того, какие данные анализируются: метрические или неметрические. Метрические данные (metric data) измеряются по интервальной или относительной шкале. Неметрические данные (nonmetric data) оцениваются по номинальной или порядковой шкале. Затем эти методы делят на классы на основе того, сколько выборок — одна, две или более — анализируется в ходе исследования. Стоит отметить, что число выборок определяется тем, как ведется работа с данными для конкретного анализа, а не тем, каким способом собирались данные.

Рис. 3.9. Классификация одномерных статистических методов [12].

Рассмотрим некоторые из перечисленных на рис. 3.9 одномерных статистических методов.

Однофакторный дисперсионный анализ

Задачей дисперсионного анализа является изучение влияния одного или нескольких факторов на рассматриваемый признак. Однофакторный дисперсионный анализ используется в тех случаях, когда есть в распоряжении три или более независимые выборки, полученные из одной генеральной совокупности путем изменения какого-либо независимого фактора, для которого по каким-либо причинам нет количественных измерений. Для этих выборок предполагают, что они имеют разные выборочные средние и одинаковые выборочные дисперсии. Поэтому необходимо ответить на вопрос, оказал ли этот фактор существенное влияние на разброс выборочных средних или разброс является следствием случайностей, вызванных небольшими объемами выборок. Другими словами, если выборки принадлежат одной и той же генеральной совокупности, то разброс данных между выборками (между группами) должен быть не больше, чем разброс данных внутри этих выборок (внутри групп).

Вариационный ряд

Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т. д. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.

Вариационный ряд — это упорядоченное распределение единиц совокупности чаще всего по возрастающим (реже по убывающим) значениям признака и подсчет числа единиц с тем или иным значением признака. Существуют следующие формы вариационного ряда: ранжированный ряд — представляет собой перечень отдельных единиц совокупности в порядке возрастания (или убывания) изучаемого признака; дискретный вариационный ряд — таблица, состоящая из конкретных значений варьирующего признака х и числа единиц совокупности с данным значением f-признака частот; интервальный ряд — значения непрерывного признака задаются интервалами, которые характеризуются интервальной частотой т.

Вариационный анализ предназначен для проверки того, существенно ли влияет изменение независимых переменных на зависимые. Например, данный метод используется для ответов на следующие вопросы:

• • влияет ли вид рекламы на объем продаж;
• • влияет ли цвет рекламного объявления на количество людей, вспомнивших рекламу;
• • влияет ли выбор сбытовой политики на величину продаж?

Статистическая проверка значимости результатов маркетинговых исследований [29].

В процессе анализа данных у исследователя регулярно возникает вопрос: достаточно ли значимы результаты исследования? Другими словами, может ли результат объясняться тем, что в выборку попали респонденты, которые нс представляют генеральную совокупность в целом? Для ответа на этот вопрос используют статистические гипотезы.

• Гипотезы — это предположения или теории, которые исследователь выдвигает относительно некоторых характеристик генеральной совокупности, подлежащей обследованию. Пользуясь статистическими приемами, исследователь пытается установить, существует ли эмпирическое доказательство, подтверждающее выдвинутые гипотезы. Проверка статистических гипотез позволяет рассчитать вероятность наступления какого-либо события. Но в условиях отсутствия полной всесторонней информации (что естественно в случаях использования данных выборки) всегда есть некоторая вероятность и ошибочного заключения.

Выдвижение гипотезы (нулевой или альтернативной). Нулевая гипотеза (H0), называемая также гипотезой status quo, представляет собой утверждение, в котором исследователь констатирует факт отсутствия каких-либо отличий либо влияний в исходных данных. Она предназначена для определения согласованности исходных данных с выдвинутым предположением. Исследователю необходимо сформулировать нулевую гипотезу так, чтобы отказ от нее приводил к желательному заключению. Например, предприятие рассматривает возможность разработки нового товара и выведения его на рынок. Для принятия положительного решения необходимо, чтобы объем продаж увеличился на 20%. Выдвинем следующее предположение: объем продаж увеличится менее чем на 20%. Это предположение и называется нулевой гипотезой и обозначается как Н0: Р? 0,20.

Альтернативная гипотеза (Ha) предназначена для определения согласованности данных с нулевой гипотезой и опровергает ее. В нашем примере против нулевой гипотезы можно выдвинуть альтернативную гипотезу вида На: Р > 0,20.

Если данные проверки гипотезы приводят к отказу от нулевой гипотезы, то принимается альтернативная гипотеза, в соответствии с которой можно ожидать увеличения объема продаж на 20%.

Существует множество методов для проверки статистических гипотез, основные методы перечислены в табл. 3.10 и впоследствии описаны с примерами.

Таблица 3.10

Статистические критерии для проверки статистических гипотез

Область применения.	Число подгрупп или выборочных совокупностей.	Виды шкал.	Критерий.	Специальные требования.	Примеры.
Гипотезы о частоте распределения.	Одна.	Номинальная.		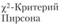Случайная выборка.	Случайны или нет наблюдаемые различия в ответах респондентов.
	Две и более.	Номинальная.	То же.	Случайная выборка, независимые выборки.	Случайны или нет различия в численности мужчин и женщин, реагирующих на продвижение товара.
	Одна.	Порядковая.	Критерий Колмогорова — Смирнова.	Случайная выборка, естественный порядок данных.	Случайно или нет распределение женщин, отдающих предпочтение определенному цвету туши (от темного до светлого).
Гипотезы о средних величинах.	Одна (большая выборка).	Метрическая (интервальная или относительная).	Z-Критерий для одной средней.	Случайная выборка, п > 30.	Случайно или нет наблюдаемое различие между выборочной оценкой средней и стандартной или ожидаемой величиной средней.
	Одна (малая выборка).	То же.	t-Критерий для одной средней.	Случайная выборка, n < 30.	Случайно или нет наблюдаемое различие между выборочной оценкой средней и стандартной или ожидаемой величиной средней. Применяется для малой выборки.
	Две (большие выборки).	´.	Z-Критерий для двух средних.	Случайная выборка, п > 30.	Случайно или нет наблюдаемое различие между средними для двух подгрупп (средний доходу мужчин и женщин).
	Две (малые выборки).	´.	ANOVA (анализ вариации).	Случайная выборка.	Случайна или нет вариация между средними для трех и более подгрупп (средняя величина расходов на развлечения для различных социальных групп).
Гипотезы о пропорциях.	Одна (большая выборка).	´.	Z- Критерий для одной пропорции.	Случайная выборка, п > 30.	Случайно или нет различие между выборочной оценкой пропорций и некоторой группой стандартных или ожидаемых оценок (процентом тех, кто собирается купить данный товар).
	Две (большие выборки).	´.	Z- Критерий для двух пропорций.	То же.	Случайно или нет наблюдаемое различие между оцениваемыми пропорциями для двух подгрупп (процентом мужчин и женщин, которые имеют высшее образование).

Перед тем как разобрать основные критерии для проверки статистических критериев, нужно установить правила принятия решений. Правила принятия решения необходимы для того, чтобы подтвердить или опровергнуть нулевую гипотезу. Эти правила в статистике называются «уровнями значимости» (а). Они являются показателями качества статистической проверки гипотез и характеризуют вероятность ошибочного заключения. А поскольку всякое решение, принимаемое на основе ограниченного ряда наблюдений, неизбежно сопровождается вероятностью ошибочного решения, важно определить, насколько велика эта вероятность. На практике часто пользуются следующими стандартными значениями а: 0,1; 0,05; 0,01; 0,005; 0,001. При фиксированном объеме выборки обычно задается величина, а — вероятность ошибочного отвержения проверяемой гипотезы Н0.

Критерии для проверки гипотез о средних величинах (Z-критерий и t-критерий). Одной из важных проблем в маркетинговых исследованиях является определение средней величины для генеральной совокупности на основе выборочных данных. Соответствующая статистическая проверка гипотезы о средней величине осуществляется с помощью Z-критерия, который используется в случае, если выборка достаточно большая (п > 30). Для малой выборки (п < 30) используется ?-критерий Стьюдента с (п — 1) степенями свободы (п — объем выборки). Для проверки гипотез о двух и более выборочных средних производится оценка различий между средними величинами.

t-Критерий для одной выборки

t-Критерий (t-test) — одномерный метод проверки гипотез, использующий ?-распределение. Применяется, если стандартное отклонение неизвестно и размер выборки мал.

t-Распределение (t-statistic) — распределение Стьюдента, симметричное колоколоподобное распределение, используемое для проверки выборок небольшого размера. При большом количестве наблюдений стремится к нормальному распределению.

t-Критерий для одной выборки позволяет проверить гипотезу о равенстве выборочного среднего некоторому заданному числу.

В так называемых одновыборочных t-критериях наблюдаемое среднее X (вычисленное по реализации выборки) сравнивается с ожидаемым (или эталонным) средним выборки? (т.е. с некоторым теоретическим средним):

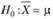
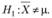
Статистика критерия:

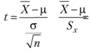
имеет t-распределение Стьюдента с (п — 1) степенью свободы.

Выборочное стандартное отклонение s оценивается по наблюдаемой реализации выборки:

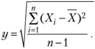
Вычисленное значение t проверяют на предмет попадания в критическую область (критическое значение можно найти по таблицам). Если вычисленное значение t попадает в критическую область, то говорят, что H0 отвергается на уровне, а в пользу альтернативы.

Например, пусть установлены некоторые фиксированные показатели эффективности деятельности торговой компании: уровень рентабельности товарооборота — 20%. Таким образом, имея данные о рентабельности (скажем, по месяцам), мы можем применить одновыборочный f-критерий для проверки гипотезы о равенстве среднего уровня рентабельности заданному значению.

Отметим, что в данном случае необходимо применить односторонний критерий, так как нарушение эффективности коммерческой деятельности произойдет только в случае снижения показателя рентабельности относительно нормативного.

Пример. Случайным образом в городе были отобраны десять магазинов. Им был предложен для продажи в течение определенного промежутка времени новый безалкогольный напиток. Компания рассчитывала на продажу 100 бутылок нового напитка в день в каждом магазине. Только в этом случае ожидаемая прибыль оправдает расходы на продвижение нового товара (табл. 3.11).

Таблица 3.11

Фактические данные об объемах продаж магазинов

1. Выдвигаем нулевую и альтернативную гипотезы:

H0: М < 100 бутылок (М — средний объем продаж в магазине за неделю).

H1 : М > 100 бутылок.

• 2. Установление допустимого уровня ошибки выборки (?). Для? = 0,05 и количеству степеней свободы 10−1=9 табличное (критическое) значение t= 2,2622.
• 3. Расчитываем стандартное отклонение:

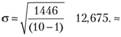
4. Расчет стандартной ошибки:

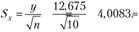
5. Расчет t-критерия:

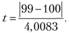
t-Критерий для двух независимых выборок

t-Критерий для двух независимых выборок (двухвыборочный f-критерий) проверяет гипотезу о равенстве средних в двух выборках (предполагается нормальность распределения переменных, а также равенство дисперсий выборок). Критерий применяется, например, если необходимо сравнить два региона по доходу на душу населения.

Алгоритм принятия решения об отклонении или не отклонении нулевой гипотезы аналогичен рассмотренному выше (одновыборочный t-критерий).

t-Критерий для двух зависимых выборок

t-Критерий для двух зависимых (парных) выборок применяется, например, для оценки эффективности работы предприятия в разные годы или после каких-то нововведений. Нулевая гипотеза также гласит об отсутствии различий (среднее значение разности наблюдений в двух группах равно нулю).

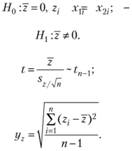
Алгоритм принятия решения об отклонении или не отклонении нулевой гипотезы аналогичен рассмотренному выше.

Z-Критерий для одной выборки

Для выводов относительно средней величины в генеральной совокупности на основе данных выборки можно использовать Z-критерий, если соблюдаются два условия:

• 1) распределение переменной в генеральной совокупности является нормальным;
• 2) объем выборки достаточно большой.

Z-Критерий основан на стандартном нормальном распределении и рассчитывается следующим образом:

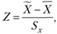
где 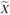- выборочная средняя; X — генеральная средняя по Н0; Sx — стандартная ошибка оценки средней величины.

При этом средняя ошибка оценки равна.

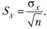
Стандартное отклонение 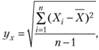где п — объем выборки.

Пример. Один из салонов красоты провел исследование по 500 клиентам, которым предложили сравнить обслуживание в данном салоне с другими, функционирующими в этом же городе. Респонденты могли выбрать следующие ответы.

Средний балл, рассчитанный по данным ответов респондентов, оказался равен 3,5, со среднеквадратическим отклонением 1,5. Может ли менеджер быть уверен в том, что в генеральной совокупности средний балл обслуживания будет не ниже 3 (средний балл по используемой шкале)?

1. Выдвижение нулевой и альтернативной гипотез:

Н0: М ? 3 (М — оценка по используемой шкале),.

Н0:М> 3.

• 2. Установление допустимого уровня ошибки выборки (?). Для? = 0,05 табличное значение Z-критерия равно 1,64.
• 3. Выборочное среднеквадратическое отклонение: ух = 1,5.
• 4. Расчет стандартной ошибки оценки генеральной средней

по формуле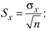

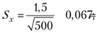
5. Расчет Z-критерия:

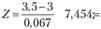
6. Принятие решения о нулевой гипотезе: нулевая гипотеза может быть отвергнута, так как расчетная величина? = 7,454 больше, чем критическая величина? = 1,64. Менеджер может быть уверен в том, что средняя оценка обслуживания выше, чем 3.

?-Критерий для двух независимых выборок

ЛПР часто бывают заинтересованы в проверке различий между группами покупателей. Если выборки сформированы случайным образом и данные одной выборки не оказывают влияния на значения другой, то такие выборки считают независимыми. В практическом маркетинге гипотезы о параметрах двух выборок используются для определения значимости различий между потребителями и теми, кто не употребляет (не использует) товар определенной торговой марки; или различий в потреблении между двумя группами людей (мужчин и женщин, городским и сельским населением, людьми с высокими и низкими доходами, холостыми и семейными, работающими и пенсионерами, жителями двух стран и др.).

Для проверки значимости различий используют Z-критерий:

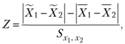
где 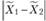- разница между средними в первой и второй выборках; 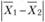- разница между средними по нулевой гипотезе; 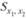- стандартная ошибка различий между двумя средними.

При этом стандартная ошибка рассчитывается исходя из среднеквадратических отклонений по отдельным группам:

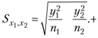
Пример. Менеджер одного из магазинов самообслуживания был уверен, что мужчины чаще посещают магазин, чем женщины. Для иллюстрации проверки гипотез о двух средних величинах вернемся к данным о 215 посетителях магазина (табл. 3.12).

Таблица 3.12

Исходные данные для проверки различий между двумя независимыми выборками

1. Выдвижение нулевой и альтернативной гипотез:

H0: Хт — Xf ? 0, среднее число посещений магазина мужчинами (Хт) такое же или меньше, чем среднее число посещений магазина женщинами (Xf). Другими словами, мужчины реже посещают этот магазин, чем женщины;

H1: Хт — Xf > 0, среднее число посещений магазина мужчинами выше, чем число посещений магазина женщинами.

2. Определение фактических различий в средних значениях показателей:

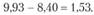
• 3. Выбор уровня ошибки выборки (а). Предположим, что допустимый уровень ошибки выборки в данном случае равен 0,05. Табличное значение Z-критерия для уровня значимости 0,05 равно 1,6449.
• 4. Среднеквадратическое отклонение составит:
  • — для мужчин

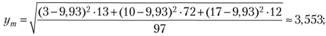
— для женщин

5. Расчет стандартной ошибки различий между двумя средними величинами по формуле.

6. Расчет статистики Z-критерия:

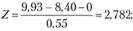
7. Формулирование выводов. Расчетное значение величины Z = 2,782 больше, чем критическое значение Z = 1,64. Нулевая гипотеза отвергается. Менеджер может сделать вывод с вероятностью 95% о том, что в среднем мужчины чаще посещают магазины самообслуживания, чем женщины.

Критерии согласия: 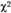-критерий для одной выборки

Для оценки случайности или существенности расхождений между частотами эмпирического и теоретического распределений используется ряд показателей, именуемых критериями согласия. Одним из основных и наиболее распространенных показателей является критерий, предложенный К. Пирсоном:

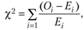
где 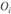- наблюдаемая частота в каждой категории; 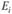- ожидаемая частота.

К. Пирсоном найдено распределение величины 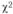и составлены таблицы, позволяющие определить предельное верхнее значение при заданном уровне значимости и числе степеней свободы, значение которого в общем случае равно количеству наблюдений за вычетом числа ограничений, необходимых для расчета статистической характеристики. Если фактическое значение 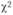меньше табличного, то расхождения между эмпирическими и теоретическими частотами считают случайными, а гипотезу о принятом законе распределения принимают.

Пример. Менеджеру магазина электронной техники необходимо проверить эффективность трех мероприятий, проводимых в магазине с целью привлечения покупателей. Он хотел бы оценить эффект каждого мероприятия по числу покупателей магазина по следующим данным.

Менеджер должен выяснить, существенны ли различия между числом посетителей магазина в различные периоды времени. На этот вопрос позволяет ответить критерий 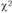. Обратимся к последовательности проведения расчета в соответствии с рассмотренным ранее процессом проверки гипотез:

1) выдвигаются нулевая и альтернативная гипотезы:

Н0: число посетителей магазина во время проведения трех мероприятий одинаковое,.

H1: существует значительная разница в численности посетителей магазина во время проводимых мероприятий;

2) определяется ожидаемое (теоретическое) число посетителей в случае, если нулевая гипотеза верна. Естественно предположить, что численность посетителей должна быть одинакова при условии отсутствия влияния других факторов.

Ожидаемое число посетителей можно определить по формуле.

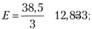
3) рассчитывается величина ?2:

• 4) выбирается уровень значимости, для которого будет найдено табличное значение 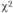. В приведенном примере число степеней свободы равно 2 (3 — 1). По специальной таблице распределения 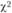определяем табличное значение 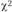для, а = 0,05 и числа степеней свободы (k — 1) = 2. В нашем случае ;
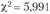• 5) сравнивается табличное значение 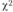с расчетным. Так как расчетное значение 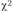больше, чем табличное значение, нулевая гипотеза отвергается. Следовательно, можно сделать вывод с вероятностью 95% о том, что посетители магазина реагируют на проводимые мероприятия. Однако такая проверка не позволяет ответить на вопрос, насколько эффективность каждого мероприятия отличается от эффективности остальных.

Критерии согласия: 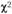-критерий для двух независимых выборок

Маркетинговым исследователям часто бывает необходимо определить, существует ли связь между двумя и более переменными. Чтобы сформулировать маркетинговую стратегию, необходимо найти ответ на вопросы: существуют ли различия в группировках мужчин и женщин на активных, умеренных и слабых потребителей или одинакова ли доля респондентов, покупающих и не покупающих данный товар, в группах с низким, средним и высоким доходом. В описанных ситуациях обычно используется 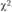-критерий для двух независимых выборок:

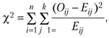
где 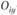- наблюдаемое число в каждой i-й строке j-ого столбца; 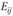- ожидаемое число в i-й строке j-ого столбца.

Пример. Менеджеру необходимо определить природу связи, если она есть, между полом покупателей и частотой посещения магазинов. Частота посещения магазинов изучалась в трех категориях:

• 1) 1−5 посещений в месяц — слабые потребители;
• 2) 6−14 посещений — умеренные потребители;
• 3) 15 и более раз — активные потребители.

Исходные данные приведены в табл. 3.12.

Среднее число посещений магазина мужчинами:

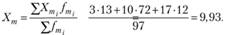
Среднее число посещений магазина женщинами:

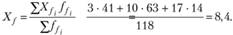
Для проведения теста необходимо:

1) сформулировать нулевую и альтернативную гипотезы:

H0: между полом и частотой посещения магазина связи нет;

H1: связь между двумя переменными существенна;

2) определить ожидаемые частоты для каждой группы, попавшей в исследование, используя итоговые данные по соответствующим строкам и столбцам (табл. 3.13);

Таблица 3.13

Расчет ожидаемых (теоретических) частот

3) рассчитать теоретическую величину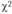

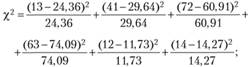
4) сравнить табличное значение 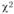с расчетным (теоретическим). Табличное значение 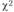(для уровня значимости 0,05 и 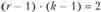степеней свободы) равно 5,991. Так как расчетное значение ( 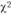= 13,35) больше, чем табличная величина, нулевая гипотеза отвергается, и можно сделать вывод о том, что существуют различия между мужчинами и женщинами по частоте посещения магазина.

Критерий Колмогорова — Смирнова

Критерий Колмогорова — Смирнова предполагает определение эмпирических накопленных частостей (долей) и сравнение их с теоретическими частостями. Он используется в тех случаях, когда исходные данные упорядочены. Точка, в которой два распределения будут иметь максимальное расхождение (по модулю), может быть использована в качестве расчетного критерия, обозначаемого через 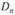и определяемого по формуле.

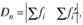
где 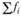- накопленные частости (доли) эмпирического распределения; 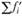- накопленные частости теоретического распределения. Величина 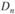, рассчитанная по данным выборки, сравнивается с критическим значением :

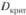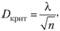
где? — критерий Колмогорова — Смирнова, соответствующий заданному уровню значимости ?, и — размер выборки.

Различным значениям соответствуют различные значения вероятностей. Эти показатели табулированы. При уровне значимости, а = 0,05 значение? для большой выборки равно 1,36. Как и для показателя ?2, считается вполне допустимым рассматривать расхождения между эмпирическими и теоретическими частотами случайными, если фактическое значение D" меньше критического значения Экрит.

Пример. Предположим, производителя красок интересует мнение потребителей о пяти новых оттенках цветов синей краски (табл. 3.14). Производителю важно знать, отдают ли потребители предпочтение какому-либо из цветов. В ходе обследования были опрошены 1000 респондентов.

Таблица 3.14

Результаты опроса респондентов относительно их предпочтений

Задача состоит в том, чтобы определить, случайно ли были отобраны цвета респондентами или приведенные данные характеризуют значительное предпочтение светлых цветов.

Тест Колмогорова — Смирнова включает следующие этапы:

1) определение нулевой и альтернативной гипотез:

Н0: потребители не отдают предпочтение ни одному из оттенков;

Н1: предпочтения потребителей существенны;

• 2) расчет теоретических накопленных частостей, соответствующих нулевой гипотезе. Нулевая гипотеза заключается в том, что не существует разницы в предпочтениях потребителей для различных оттенков нового цвета. Если это так, то доля лиц, отдающих предпочтение каждому из оттенков, должна быть равна 1/5 (или 0,2);
• 3) расчет эмпирических накопленных частостей по данным выборки.

В табл. 3.15 приведены необходимые для расчета критерия данные.

Таблица 3.15

Данные для расчета критерия Колмогорова — Смирнова

4) выбор уровня значимости ?.

При уровне значимости 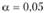критическое значение? равно 1,36, следовательно, для большой выборки 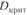определяется по формуле.

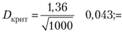
5) определение фактического значения Dn, равного максимальному абсолютному отклонению между теоретическими и эмпирическими частостями.

Наибольшая абсолютная разность равна 0,24, которая и является величиной Dn по критерию Колмогорова — Смирнова;

6) сравнение расчетного значения Dn и критического значения 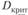. Принятие решения о нулевой гипотезе.

Так как расчетное значение 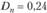превосходит критическое значение 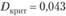, нулевая гипотеза об отсутствии предпочтений отвергается: респонденты предпочитают светлые тона.

3.4.3.2. Многомерные статистические методы

Многомерные статистические методы прекрасно подходят для анализа данных, если для оценки данных каждого элемента выборки используются два или больше измерителей, а эти переменные анализируются одновременно. Многомерные методы отличаются от одномерных прежде всего тем, что при их использовании центр внимания смещается с уровня (средних показателей) и распределений (дисперсий) явлений и сосредоточиваются на степени взаимосвязи (корреляции или ковариации) между этими явлениями.

Многомерные статистические методы (multivariate techniques) — методы статистического анализа, применяемые для анализа данных, если для оценки каждого элемента выборки используются два или больше измерителя и эти переменные анализируются одновременно (рис. 3.10). Данные методы применяются для определения одновременных взаимосвязей между двумя или больше явлениями.

Рис. 3.10. Классификация многомерных статистических методов [12].

Кросс-табуляция (cross-tabulation) — статистический метод, при котором одновременно характеризуются значения двух или более переменных. Кросс-табуляция заключается в создании таблиц сопряженности признаков, отражающих совместное распределение двух или более переменных с ограниченным количеством категорий или определенными значениями.

Дисперсионный анализ (variance analysis) — метод в математической статистике, направленный на поиск зависимостей в экспериментальных данных путем исследования значимости различий в средних значениях. В отличие от t-критерия позволяет сравнивать средние значения грех и более групп. Разработан Р. Фишером для анализа результатов экспериментальных исследований. В литературе также встречается обозначение ANOVA (ANalysis Of VAriance).

Обобщенно задача дисперсионного анализа состоит в том, чтобы из общей вариативности признака выделить три частные вариативности:

• 1) вариативность, обусловленную действием каждой из исследуемых независимых переменных;
• 2) вариативность, обусловленную взаимодействием исследуемых независимых переменных;
• 3) вариативность случайную, обусловленную всеми неучтенными обстоятельствами.

Ковариационный анализ (analysis of covariance) — тесно связанный с дисперсионным анализом статистический метод, в котором зависимая переменная статистически корректируется на основе связанной с ней дополнительной информации, с тем чтобы устранить вносимую извне изменчивость и таким образом повысить эффективность анализа.

Дискриминантный анализ (discriminant analysis) — метод для анализа данных маркетинговых исследований в том случае, когда зависимая переменная категориальная, а предикторы (независимые переменные) интервальные. Цель дискриминантного анализа — это различение (дискриминация) объектов наблюдения на классы по заранее определенным признакам.

Регрессионный анализ (regression analysis) — статистический метод исследования влияния одной или нескольких независимых переменных х1, х2, …, xp на зависимую переменную у. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Цели регрессионного анализа:

• • определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными);
• • предсказание значения зависимой переменной с помощью независимой (независимых);
• • определение вклада отдельных независимых переменных в вариацию зависимой.

Корреляционный анализ (correlation analysis) — статистический метод, выявляющий взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной.

Факторный анализ (factor analysis) — метод многомерной математической статистики, применяемый при исследовании статистически связанных признаков с целью выявления определенного числа скрытых от непосредственного наблюдения факторов. Цель факторного анализа — наблюдая большое число измеряемых переменных, выявить небольшое число латентных макропеременных-факторов, которые в основном определяют поведение измеряемых переменных.

Кластерный анализ (cluster analysis) — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы. Цель кластерного анализа — разбиение наблюдений, респондентов (строк матрицы данных) на относительно однородные кластеры, исходя из рассматриваемого набора переменных, таким образом, что в один кластер попадают схожие, близкие, а в разные — далекие друг от друга наблюдения.

Многомерное шкалирование (multidimensional scaling) — метод анализа данных, позволяющий располагать точки, соответствующие изучаемым объектам (шкалируемые объекты), в некотором (как правило, евклидовом) многомерном «признаковом» пространстве, так, чтобы попарные расстояния между точками в этом пространстве как можно меньше отличались от эмпирически измеренных попарных мер «близости» этих изучаемых объектов. Каждой оси этого пространства соответствует шкала, например интервальная. Критерий отличия этих двух величин называется функцией стресса. Если элементы матрицы близостей получены по интервальным шкалам, метод многомерного шкалирования называется метрическим. Когда аналогичные шкалы являются порядковыми, метод многомерного шкалирования называется неметрическим. Цель многомерного шкалирования — поиск и интерпретация «латентных (т.е. непосредственно не наблюдаемых) переменных», дающих возможность пользователю объяснить сходства между объектами, заданными точками в исходном пространстве признаков.

Выбор определенного метода анализа зависит, кроме характера и направлений связей с переменными и уровня шкалирования, от решаемой проблемы. В табл. 3.16 представлены рекомендации по выбору метода анализа для решения типичных задач маркетинга в компании.

Многомерный статистический анализ — это трудоемкий процесс, который фактически невозможно провести без статистических программных продуктов. Существует около тысячи распространяемых на мировом рынке пакетов, решающих в том или ином поле задачи статистического анализа данных. Большую часть статистических пакетов можно разбить на две группы — это статистические пакеты общего назначения (универсальные пакеты) и специализированные пакеты.

Таблица 3.16

Рекомендации по применению методов анализа [14]

Универсальные пакеты — предлагают широкий диапазон статистических методов. В них отсутствует ориентация на конкретную предметную область. Они обладают дружественным интерфейсом. Из зарубежных универсатьных пакетов наиболее распространены В AS, SPSS, Systat, Minilab, Statgraphics, STATISTICA.

Специализированные пакеты — как правило, реализуют несколько статистических методов или методы, применяемые в конкретной предметной области. Чаще всего это системы, ориентированные на анализ временны? х рядов, корреляционно-регресионный, факторный или кластерный анализ. Применять такие пакеты целесообразно в тех случаях, когда требуется систематически решать задачи из этой области, для которой предназначен специализированный пакет, а возможностей пакетов общего назначения недостаточно. Из российских пакетов более известны STADIA, Олимп, Класс-Мастер, КВАЗАР, Статистик-Консультант; американские пакеты — ODA, WinSTAT, Static и т. д.

Стандартные статистические методы обработки данных включены в состав электронных таблиц, таких как Excel, Lotus 1−2-3, QuattroPro, и в математические пакеты общего назначения, например Mathcad.