Среднее. 
Основы теории и практики обработки экспериментальных данных

Среднее показывает «центральное положение» (центр) переменной и рассматривается совместно с доверительным интервалом. Обычно интерес представляют статистики (например, среднее), дающие информацию о популяции в целом. Чем больше размер выборки, тем более надежна оценка среднего. Чем больше изменчивость данных (больше разброс), тем оценка менее надежна.

Среднее: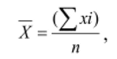

где п — число наблюдений (объем выборки).

При анализе вариационных рядов смещение от центра и крутизну распределения характеризуют специальные показатели. Эмпирические распределения, как правило, смещены от центра распределения вправо или влево, асимметричны. Нормальное распределение строго симметрично относительно средней арифметической, что обусловлено четностью функции.

Асимметрия распределения возникает вследствие того, что какиелибо факторы действуют в одном направлении сильнее, чем в другом, или процесс развития явления таков, что доминирует какая-то причина. Кроме того, природа некоторых явлений такова, что имеет место асимметричное распределение.

Наиболее простой мерой асимметрии является разность между средней арифметической, модой и медианой:

• — в симметричном ряду: X = Мо = Ме
• — при правосторонней асимметрии: Мо <�Ме< X;
• — при левосторонней асимметрии: Мо >Ме> X.

Для определения направления и величины смещения (асимметрии) распределения рассчитывается коэффициент асимметрии, представляющий собой нормированный момент третьего порядка: Л. у=т/.у, При левосторонней асимметрии коэффициент асимметрии (АбсО), при правосторонней (Л$>0).

Если вершина распределения сдвинута влево и правая часть ветви оказывается длиннее левой, то такая асимметрия является правосторонней, в противоположном случае левосторонней.

Соотношение между модой, медианой и средней арифметической в симметричном и асимметричном рядах позволяет в качестве меры асимметрии использовать более простой показатель коэффициента асимметрии Пирсона:

Если К_а>0, то асимметрия правосторонняя, если К_а<0, то асимметрия левосторонняя, при К_а=0 ряд считается симметричным.

Более точно асимметрию можно определить, используя центральный момент третьего порядка:

Если А_г > 0, то асимметрию можно считать значительной, если А_г< 0,25 асимметрию можно считать не значительной.

Для характеристики степени отклонения симметричного распределения от нормального по ординате используется показатель островершинности, крутизны распределения, называемый эксцессом:

где т₄ — центральный момент четвертого порядка.

Для нормального распределения:

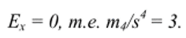
где т₄ -центральный момент четвертого порядка.

У высоковершинных кривых эксцесс положительный, у низковершинных отрицательный (рисунок 5.4).

Показатели эксцесса и асимметрии необходимы в статистическом анализе данных для определения неоднородности совокупности, асимметричности распределения и близости эмпирического распределения к нормальному закону. При значительных отклонениях показателей асимметрии и эксцесса от нуля нельзя признать совокупность однородной, а распределение близким к нормальному. Сопоставление фактических кривых с теоретическими позволяет математически обосновать полученные статистические результаты, установить тип и характер распределения социально-экономических явлений, прогнозировать вероятность появления изучаемых событий.