Показатели точности системы

Точность системы характеризуется величинами ошибок в установившемся режиме работы системы, т. е. для моментов времени много больших времени переходного процесса t «/_п.

При действии на линейную систему в установившемся режиме ее работы регулярного задающего воздействия х (Г) и случайной помехи/(/) в соответствии с принципом суперпозиции результирующая ошибка е_уст(/) складывается из двух составляющих: регулярной в_рег(/) и случайной е_сл(/). Изображение результирующей ошибки е_уст (t) для системы, представленной структурной схемой (см. рис. 2.1), определяется выражением.

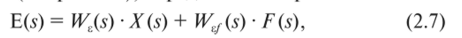
где T (s) — изображение входного воздействия x (t); F (s) — изображение помехи/(/).

Передаточные функции W_r(s), lV_c/(s) ошибок системы задаются формулами (2.2) и (2.3).

Ошибки по регулярному задающему воздействию x (t)

Изучение свойств точности системы проводится по результатам анализа ошибок для трех пробных регулярных входных воздействий:

Для расчета характеристик точности системы часто используют приближенный метод коэффициентов ошибок при условии:

• • когда задающее воздействие является медленно меняющейся функцией времени по сравнению со временем переходного процесса системы;
• • ошибки рассчитываются в установившемся режиме работы системы, т. е. для моментов времени, намного превышающих время переходного процесса, t «t_n.

Эти допущения позволяют ограничиться тремя слагаемыми при разложении передаточной функции W_r(s) по степеням s относительно 5 = 0:

где у₀, у, у₂ — коэффициенты ошибок по постоянной составляющей задающего воздействия x (t), по его скорости и ускорению соответственно.

С учетом формулы (2.7) и разложения (2.8) при отсутствии случайной составляющей ошибки (F (s) = 0) получим выражение.

и, применяя обратное преобразование Лапласа к обеим частям этого уравнения, получим формулу для вычисления регулярных ошибок в установившемся режиме работы системы при заданном входном воздействии х =x (t):

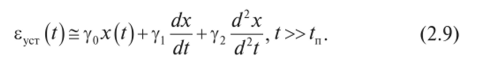
Итак, согласно формуле (2.6) и разложению (2.8) получим.

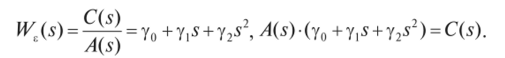
Подставляя в последнее выражение значения полиномов Л (5) и С (5), после некоторых преобразований значения коэффициентов ошибок у₀, у, у₂ вычисляют в результате приравнивания коэффициентов при одинаковых степенях5левой и правой частей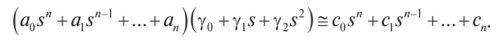

Так, формируются три уравнения для определения этих коэффициентов ошибок:

Таким образом, для повышения точности системы следует [3, разд. 2.7.3, с. 92]:

• • повышать ее порядок астатизма (порядок астатизма системы определяется числом интегрирующих звеньев передаточной функции W (s)). Ошибки по постоянной составляющей входного воздействия астатических систем (при x (t) = а) всегда равны нулю, так как для них коэффициент ошибки у₀ = 0. Для астатической системы второго порядка ошибка и по скорости входного воздействия равна нулю, так как для этой системы у, = 0;
• • повышать коэффициент усиления к системы в разомкнутом состоянии.