Производительность дробилок вибрационного действия

Щековые вибрационные дробилки, в конструктивном варианте представленном на рис. 26, обеспечивают более интенсивную разгрузку дробленого материала, по сравнению с обычными щековыми машинами. Это достигается согласованным движением щек сверху вниз в момент раскрытия камеры дробления.

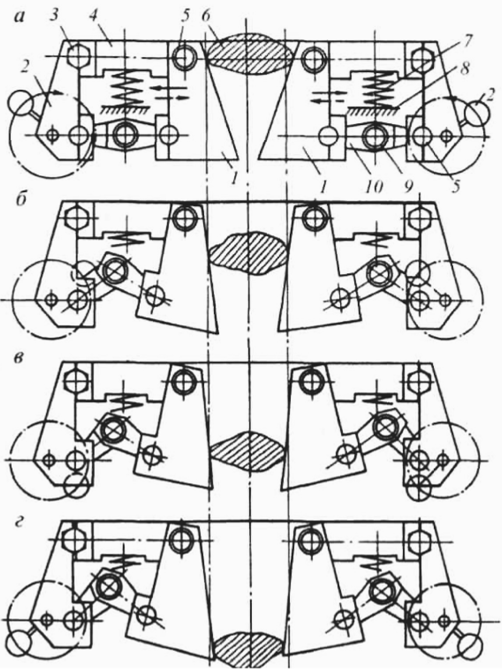
Рис. 26. Схема последовательности выгрузки дробленого материала из рабочей камеры.

Здесь высота призмы выпадения дробленого материала определяется не только расстоянием, пройденным материалом за время отхода щеки, но и тем отрезком пути, на который переместилась вверх сама дробилка относительно выпадающего 44.

материала. Кроме того, объему выпадающего материала придается дополнительно перемещение за счет скорости, которая сообщается материалу при повороте щек на разгрузку. Таким образом, общий путь или высота призмы измельченного объема материала, который выходит из дробилки за время отхода щеки, определяется как сумма трех слагаемых:

где И, — путь пройденный объемом выгружаемого материала, при свободном падении. Н, = l/2gt²; Н₂ — путь равный вертикальной амплитуде колебаний дробящего механизма. Н₂ = 2Р/Мдр • ю²; где 2Р —усилие, развиваемое дебалансами, Н; Мдр —масса дробящего механизма, кг; ш — частота вращения дебаланса, 1 /с.; Н₃ — дополнительный путь, определяемый скоростью выталкивания материала из камеры дробления;

Объем призмы выпадающего материала за цикл — V= L i> Нобщ, м³, где L—длина щеки, м; о — разгрузочная щель, м; и = S + 2В*ср; S — разгрузочная щель при неработающем режиме, м; В — расстояние от оси подвеса щеки до разгрузочной щели, м; ф — угол поворота щеки, рад.

Производительность ударно-вибрационной дробилки определяется как объем призмы выпадения раздробленного материала на число циклов в единицу времени.

где р = 0,65 — коэффициент разрыхления материала, у — плотность дробимого материала, т/м³; п — частота вращения дебалансного вала, 1/мин.