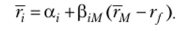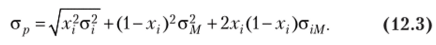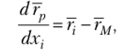Неравновесные и равновесные модели

Очевидно, что доходности ценных бумаг, обращающихся на рынке, можно рассматривать в зависимости от времени. При этом будут зависеть от времени числовые характеристики случайной величины г_р Также, вообще говоря, будут зависеть от времени и значения параметров аир.

Модель финансового рынка называется равновесной, если числовые характеристики входящих в нее случайных величин постоянны во времени. Экономический смысл подобного предположения очевиден: рынок считается «устоявшимся», сбалансированным. В этом случае можно получить некоторые конкретные результаты, существенно упрощающие ситуацию.

Будем рассматривать модель зависимости доходности ценной бумаги от доходности касательного портфеля (предполагается, что безрисковая ставка получения и предоставления займов для всех участников рынка одна и та же и равна гу). Если модель равновесная, т. е. рынок сбалансированный, то касательный портфель удовлетворяет следующему свойству, доля каждой ценной бумаги в нем соответствует ее относительной рыночной стоимости. Такой портфель называется рыночным и определяется однозначно. Таким образом, рассматривая равновесные модели, мы будем отождествлять понятия касательного и рыночного портфеля, доходность которого обозначим г_м.

Итак, регрессионная модель для i-й ценной бумаги имеет вид:

Оказывается, в равновесном случае имеет место следующая теорема.

Теорема. Для всех ценных бумаг, обращающихся на рынке, коэффициент сц один и тот же и равен безрисковой ставке.

Имеем.

Рассмотрим портфель р, состоящий из t-й ценной бумаги и рыночного портфеля М в пропорции г, и 1 — х_{ соответственно. Ожидаемая доходность такого портфеля составит:

а стандартное отклонение будет.

Все такие портфели отображаются на кривую, соединяющую точки i и М (рис. 12.3).

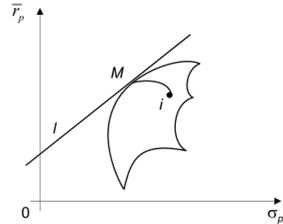
Рис. 12.3.

Из равенства (12.2) получаем:

а из равенства (12.3): откуда

Но кривая касается прямой I, поэтому.

Приравняв правые части равенств (12.4) и (12.5), получим.

Таким образом, единственным параметром, характеризующим данную ценную бумагу, является ее чувствительность к рыночному портфелю.