Примеры расчетов обтекания затупленных тел

Рассмотрим некоторые примеры расчета сверхзвукового обтекания затупленных тел относительно простой формы (сфера, цилиндрический торец и т. п.) для дальнейшего уточнения постановок задач обтекания и иллюстрации возможностей используемых численных методов. Помимо чисто методических целей, эти примеры представляют самостоятельный интерес.

При стационарном обтекании передней части затупленных осесимметричных тел однородным по пространственным координатам потоком невязкого, нетеплопроводного газа определяющими параметрами являются число Маха набегающего потока Моо, углы атаки, а и скольжения 0, а также молекулярный состав газа, в частности, показатель адиабаты к, если принимается модель совершенного газа. Выбирая за характерные размерные величины линейный размер тела ?, плотность р* _р и скорость набегающего потока газа V«р, обезразмерим газодинамические параметры следующим образом:

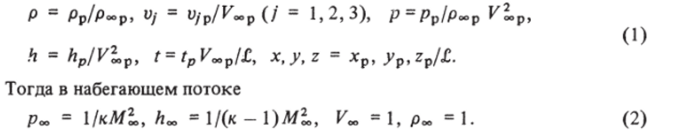
В сферической системе координат (1.12) выражения для компонент вектора скорости набегающего потока принимают вид.

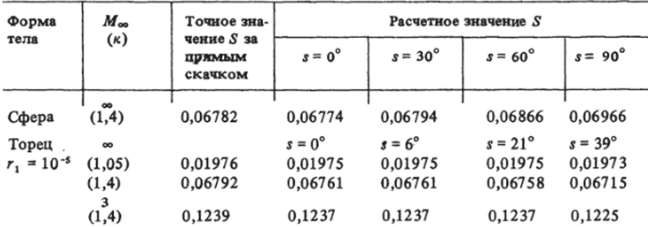
1. На основе изложенного в предыдущем разделе алгоритма были проведены систематические расчеты сверхзвукового пространственного обтекания ряда затупленных тел в основном с сегментально-коническими затуплениями. Предельные формы таких затуплений — сфера и цилиндрический торец. Расчет обтекания этих тел выполнен многими авторами, начиная с известной работы [120]. Укажем в качестве примера также работы [13, 17, 18, 20, 21, 45, 47, 52, 121], в которых на основе метода интегральных соотношений [122], метода прямых [123], метода распада разрывов [124], метода сеток [29], метода крупных частиц [125, 126], сеточно-характеристического метода [50] и других рассматривалось осесимметричное и пространственное обтекание различных затуплений. Здесь рассматривается обтекание этих предельных форм, при этом преследуются в основном методические цели — оценка точности расчетных данных, выбор значений сеточных параметров и т. п.

Характерная картина осесимметричного обтекания цилиндра с плоским затуплением (цилиндрического торца) и поведение газодинамических параметров в ударном слое представлены на рис. 5.3−5.6 для случая - = ⁰⁰, к = 1.4. Показаны линии постоянного давления р = const (рис. 5.3), изохоры р = const (рис. 5.4), линии М = const (рис. 5.5) и характеристики первого и второго семейства в сверхзвуковой области течения (рис. 5.6). Расчеты проведены в сферической системе координат (1.12) методом установления от довольно произвольных начальных данных, задаваемых в виде начальной формы ударной волны (параболоид), линейного распределения скорости по поверхности тела и линейного распределения газодинамических параметров между телом и ударной волной.

В табл. 1 иллюстрируется характер установления ударной волны и параметров в ударном слое для цилиндрического торца без скругления кромки (r_t = 1СГ⁵) и со скруглением (фаской) r_t = 0,5. Линейные размеры отнесены к радиусу цилиндра. В зависимости от безразмерного времени t и числа шагов по времени п приведены максимальные значения скорости ударной волны max | Nⁿ_cm I (см. 1.16) и производных по времени от газо.

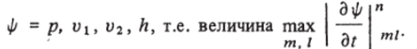
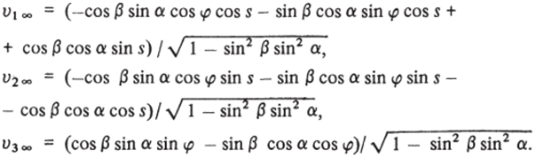
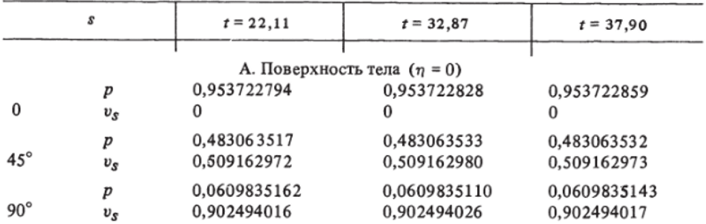
динамических параметров Индекс т соответствует узлам разностной сетки по азимутальному углу s, I — поперечному направлению. Для установления параметров с 4 знаками требуется обычно 600−1000 шагов по времени. В табл. 2 представлена более поздняя стадия установления для случая сферы, обтекаемой при числе Маха набегающего потока воздуха М_ж = 3. Здесь показано установление ударной волны R_Ci а также давления р и компонент вектора скорости Vi = v_Si v₂ = у г ^ПР^И некоторых значениях азимутального угла на поверхности тела (т? = 0) и ударной волне (т? = 1).

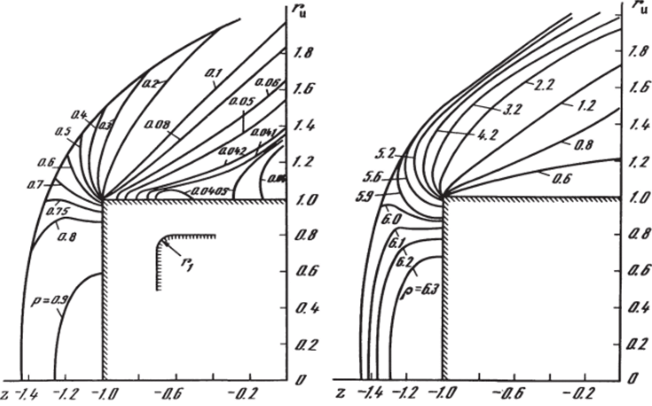
Рис. 5.3 Рис. 5.4

Рис. 5.5 Рис. 5.6

Как отмечалось, используемая в этих расчетах схема является недивергентной, поэтому выполнение интегральных законов сохранения может служить для дополнительного контроля точности расчетов. В табл. 3 для некоторых режимов обтекания сферы и цилиндрического торца приведены значения энтропийной функции pjff за прямым скачком уплотнения и Установление ударной волны и поля течения при сверхзвуковом обтекании цилиндрического торца Mot, =", к = 1,4.

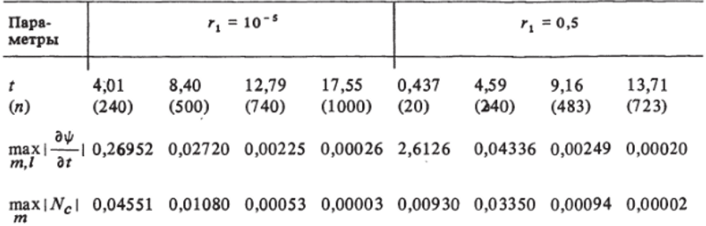
Таблица 2.

Установление параметров при обтекании сферы (А, = я/40, Л_а = 0,05) Л/ = 3, к = 1,4.

вычисленные по величине давления на поверхности тела, а также расход газа между телом и ударной волной через сечение s = const, вычисленный по установившимся в ударном слое параметрам (расчет) и соответствующее его значение через поверхность ударной волны до этих же сечений s = const (точное). Приведенное сравнение показывает вполне удовлетворительное совпадение.

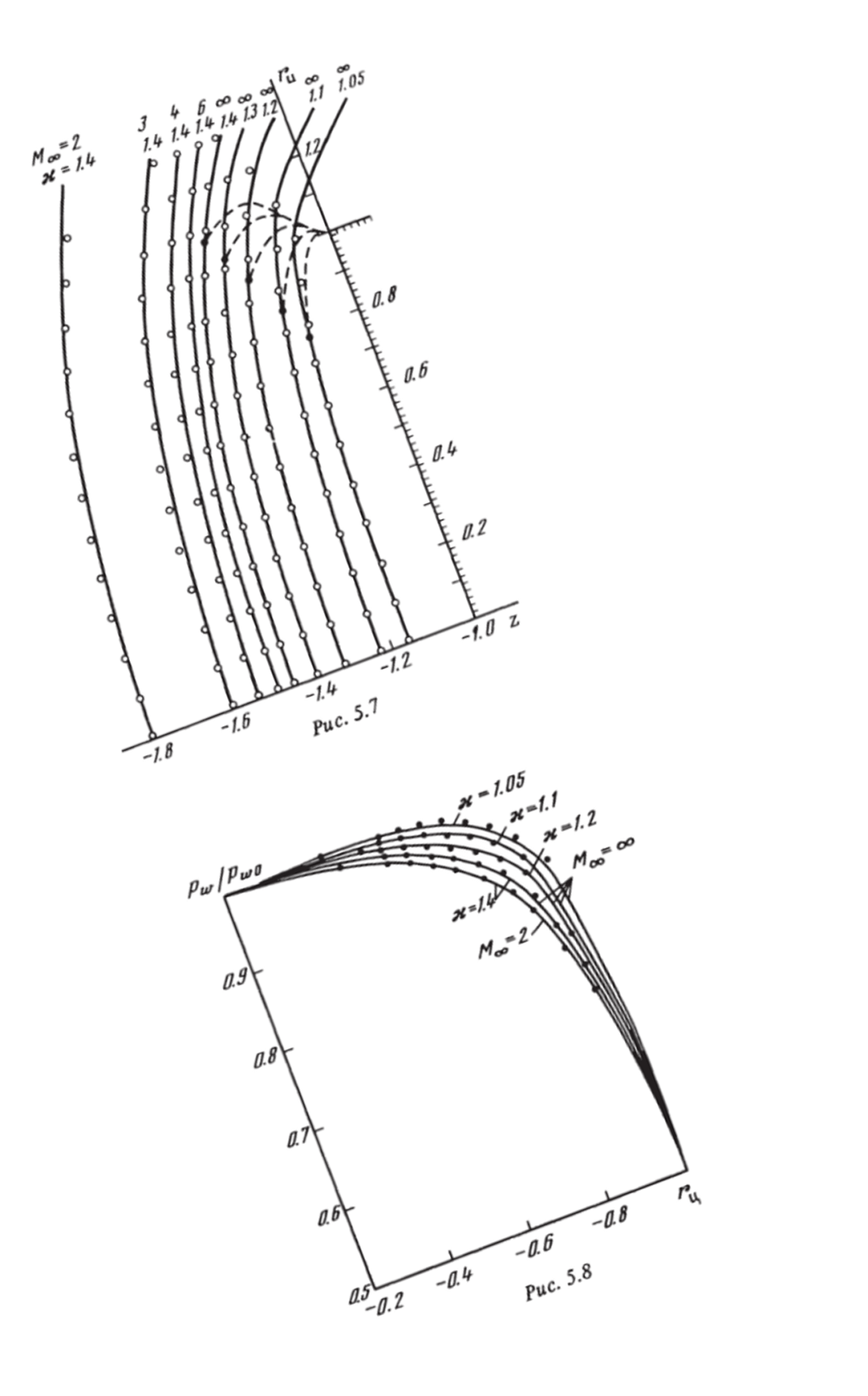
Влияние сеточных параметров на распределение давления в ударном слое для случая обтекания сферы при числе Маха Мао = 3 и показателя адиабаты к = 1,4 показано в табл. 4. Систематические расчеты обтекания торца проведены на сетке с 61 узлом по координате 5 и 16 узлами в поперечном направлении, что обеспечивает точность расчетных данных в пределах 1—2% всюду, вне малой окрестности угловой точки. На рис. 5.7, 5.8 показано влияние числа Маха набегающего потока -Мао и показателя адиабаты к на картину обтекания (рис. 5.7) и распределение давления по лобовой поверхности цилиндрического торца (рис. 5,8). Расчетные данные обозначены сплошными и штриховыми кривыми. Точками отмечены данные, полученные формальной аппроксимацией расчетных значений. В частности, форма ударной волны удовлетворительно может быть описана формулой.

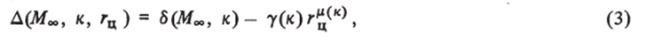
Таблица 3.

А. Энтропийная функция S = р/р^к на теле.

Б. Расход через сечения s = const.

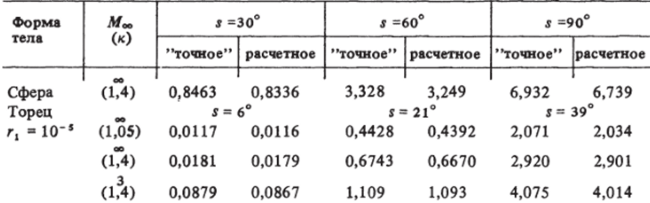
Влияние сеточных параметров на распределение давления в ударном слое при обтекании сферы Мао = 3, к = 1,4.

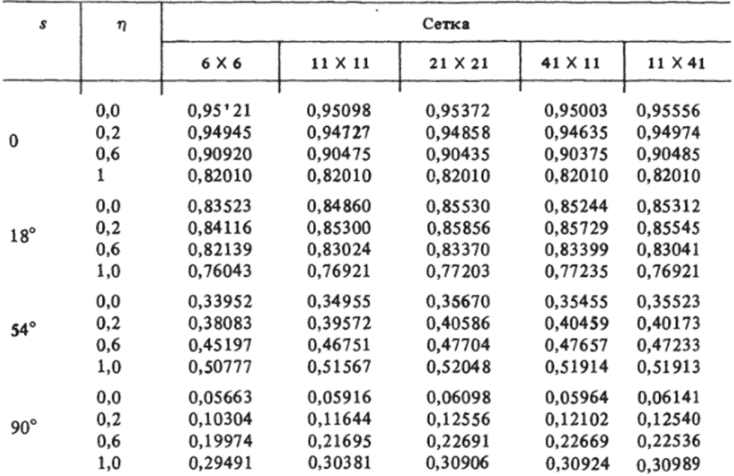
где 6(Л/оо, к) = 8 о (к) + 1,39/Afl — отход ударной волны вдоль оси симметрии потока, у (к) = 0,24е^0,3, ц (к) = 0,2/ >/еГ + 2,12, е = (к — 1)/(к + 1). Зависимость 6₀ (к) = /Т (1 + 0,6е) взята из работ [47, 127]. Вычисленные по формуле (3) значения отхода ударной волны показаны светлыми точками на рис. 5.7, темными точками отмечено положение звуковых точек на ударной волне, полученное с использованием соотношений (3).

Для давления на теле может быть предложена следующая формула, аппроксимирующая расчетные данные с точностью 2−3%: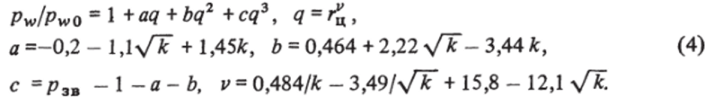

Здесь p_w — давление на теле, p_Wo — давление торможения, обезразмерен ные в соответствии с (1),.

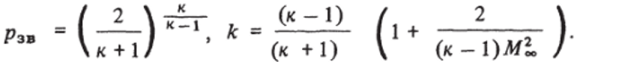
Интегрируя (4), можно получить следующее выражение для коэффициента волнового сопротивления:

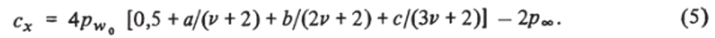
Соответствующая зависимость с_х от обозначена сплошной линией на.

°$.

рис. 5.9 (верхняя кривая). Точками нанесены данные из численного решения задачи при различных значениях чисел Маха Л/*, и показателях адиабаты к.

Влияние числа Маха М_ж и показателя адиабаты к на распределение давления по боковой поверхности цилиндрического торца показано на рис. 5.10 (к * 1,4) и 5.11 (Л/оо = °°). Штриховая линия на рис. 5.11 соответствует расчету с учетом равновесных физико-химических превращений в ударном слое (Г* = 5 км/с, Н = 30 км), точки на рис. 5.10 — экспериментальные данные из работы [128]. Следует отметить, что в большинстве рассмотренных вариантов непосредственно за угловой точкой градиент давления положительный, что способствует отрыву пограничного слоя в угловой точке. Поэтому реальное поведение давления непосредственно за угловой точкой отличается от полученного в рамках невязкого, нетеплопроводного газа. Выход на экспериментальные значения наблюдается на расстояниях порядка единицы от угловой точки, как показывает сравнение, приведенное на рис. 5.10. На рис. 5.12 показано влияние радиуса скругления кромки (фаски) г_х на распределение давления по боковой поверхности (Л/оо = °°, к = 1,4).

2. В качестве второго примера стационарных задач рассмотрим сверхзвуковое пространственное обтекание цилиндрического торца с небольшим скруглением сильно недорасширенной струей невязкого, нетеплопроводного газа, истекающего из сверхзвукового сопла в вакуум [62, 129]. Для тел более простой формы и плоских преград подобные задачи рассматривались, например, в работах [130—137].

В довольно широком диапазоне параметров задачи (форма тела, взаимное расположение сопла и тела, параметров на срезе сопла и др.) реализуется картина обтекания с отошедшей ударной волной, отделяющей область ''невозмущенного" потока газа в струе от области, в которой проявляется влияние тела (''ударный слой"). В этом случае вначале можно рассчитывать поле от струи, истекающей в вакуум, а затем воспользоваться полученными данными в качестве граничных условий на поверхности ударной волны для расчета смешанного течения в ударном слое. Для решения первой задачи использовалась предложенная в работе [138] аналитическая аппроксимация поля течения в струе. В этой аппроксимации поток считается радиальным и изоэнтропическим, причем в каждой точке на расстоянии г от среза сопла плотность аппроксимируется выражением.

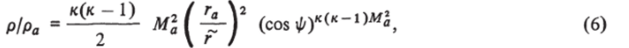
которое хорошо согласуется с экспериментом при больших значениях чисел Маха на срезе сопла М_а, начиная с расстояний в несколько радиусов среза сопла г_а внутри телесного угла ф < ф₀ = 60° (рис. 5.13). Здесь р_а — плотность на срезе сопла, ф — угол между осью сопла и направлением в рассматриваемую точку, г — расстояние от среза сопла до рассматриваемой точки. Другие газодинамические параметры определяются естественным образом с учетом сделанных предположений о радиальности и изоэнтропийности потока. Постановка второй задачи и метод ее решения ничем не отличаются от рассмотренной в разд. 1 настоящей главы, с учетом того факта, что теперь параметры перед ударной волной являются переменными.

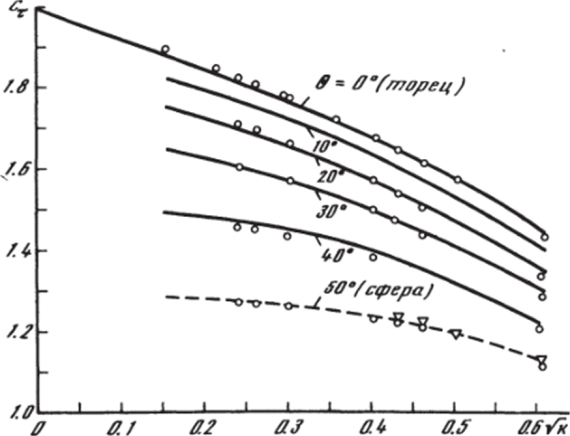
Рис. 5.9.

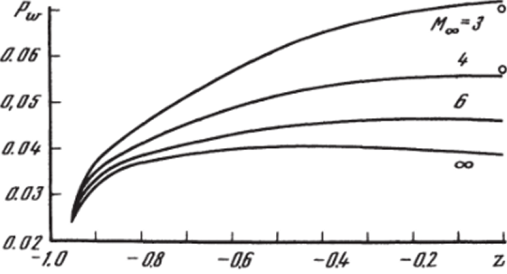
Рис. 5.10.

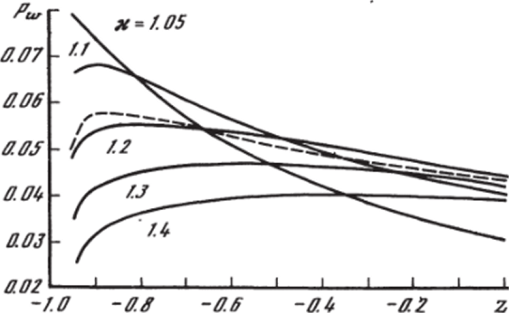
Рис. 5.11.

со со.

Рис. 5.14

в силу неоднородности набегающего потока и берутся из выражения (6), а также не учитывается вдув.

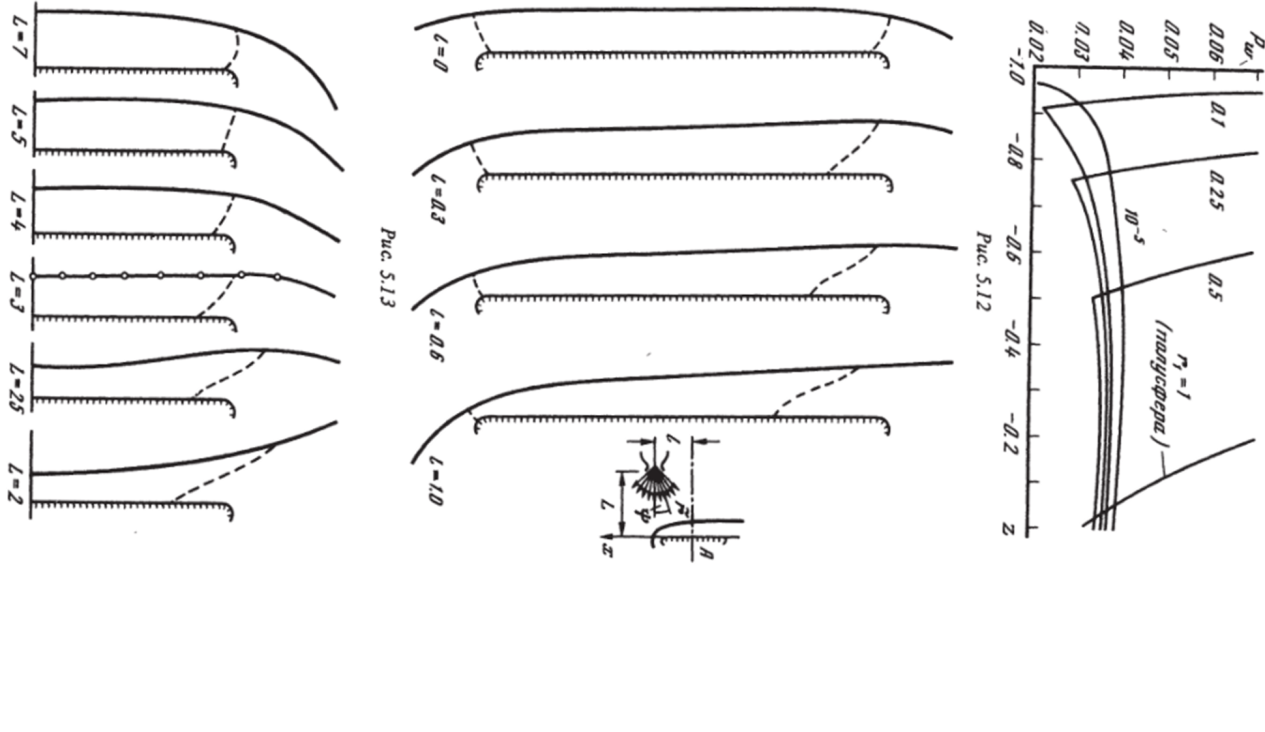
На рис. 5.13—5.19 представлены некоторые результаты численных расчетов, выполненных Г. Аксеновым в описанной выше постановке для сверхзвукового сопла с параметрами на срезе сопла М_а =4,3, к = 1,35, г_а =0,05. Линейные размеры отнесены к радиусу обтекаемого цилиндра с плоским срезом, давление отнесено к величине р_а V%, где V_а — скорость газа на срезе сопла. На рис. 5.14 показано влияние расстояния от среза сопла до тела L на форму ударной волны в случае осесимметричного обтекания (оси симметрии сопла и тела совпадают). Видно, что с уменьшением этого расстояния форма ударной волны трансформируется от обычной для обтекания этого тела однородным потоком газа (L 7−9) до соответствующей картины нормального натекания струи на плоскую преграду (L ^ 2—3). При этом звуковая точка на теле постепенно смещается со скругления к оси тела и часть обтекаемого тела вблизи скругления уже не влияет на параметры в трансзвуковой области течения. Для случая L = 3 точками нанесены данные расчета с вдвое меньшим шагом И_г сетки по угловой координате. Величина отхода ударной волны на оси тела 6 в зависимости от величины L показана на рис. 5.15. Кривая 1 соответствует численному решению, кривая 2 — приближенному решению из работы [138].

Для одного из значений L = 4 на рис. 5.13 показано влияние смещения между осями тела и сопла / (которые выбирались параллельными) на картину обтекания в плоскости симметрии потока. С увеличением этого смешения звуковая точка на теле в плоскости симметрии потока на подветренной стороне также смещается к оси тела, а в наветренной стороне — к кромке тела, причем здесь это смещение незначительно, в отличие от подветренной стороны.

Влияние параметров задачи L и /. на распределение давления по телу в плоскости симметрии потока (сплошные кривые) можно увидеть на рис. 5.16 (/ =0) и 5.17 (/ = 0,6). Видно, что с увеличением L распределение давления становится более ''плоским" и, начиная с L ^ 9, практически не отличается от соответствующего распределения для случая обтекания однородным потоком (соответствуют темные точки на рис. 5.16). Светлыми точками на рис. 5.16, 5,17 отмечено звуковое давление. Вместе с локальными газодинамическими параметрами вычислялись также суммарные аэродинамические коэффициенты с_т и — проекции равнодействующей сил давления на оси г их соответственно, отнесенные к р_а V ²J 2, а также момент этой силы с_т относительно точки, А (рис. 5.13), отнесенный к Pa^l^ll2. На рис. 5.18, 5.19 показано влияние взаимного расположения среза сопла и обтекаемого тела на аэродинамические коэффициенты. Здесь для различныхL и / приведены значения с_Т (рис. 5.18), c_N (рис. 5.19, сплошные кривые) и с_т (рис. 5.19, штриховые линии). Видно, что при изменении L от 2 до 7 эти коэффициенты. уменьшаются на порядок, т. е. именно на этих расстояниях обтекаемое тело получает основную часть импульса от струи. Зависимость от / при изменении этого параметра в пределах 0—1 сравнительно слабая (рис. 5.18, штриховые линии).

3. В качестве примера нестационарного обтекания тел рассмотрим задачу о продольных колебаниях сферы и цилиндрического торца в сверхзвуковом потоке газа [139].

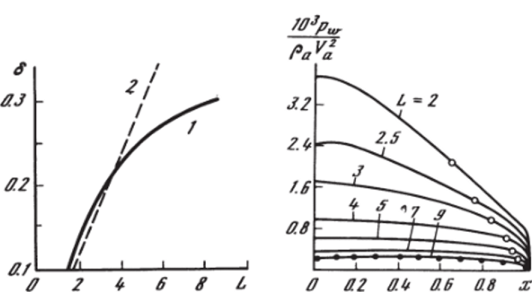
Рис. 5.15 Рис. 5.16

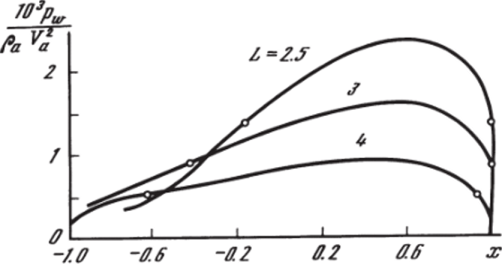
Рис. 5.17

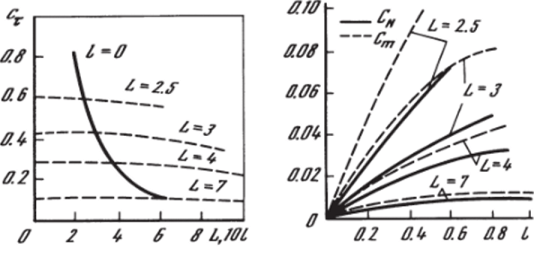
Рис. 5.18 Рис. 5.19

При исследовании нестационарного обтекания тел (неравномерное движение тела) с малыми возмущениями относительно некоторых средних значений можно использовать линейную теорию, в частности, метод аэродинамических производных [140]. В такой постановке сверхзвуковое обтекание затупленных тел рассматривалось для самых разнообразных типов возмущений. В качестве примера можно указать работы [141−147].

В общей нелинейной постановке задача описана, например, в разд. 1 этой главы, следует учесть только, что при использовании жестко связанной с обтекаемым телом системы координат x_it х₂, х₃ в дополнение к выписанным в соотношениях (1.11) выражениям для f = }/i, /2, /3 I следует добавить члены, связанные с переносной скоростью движения системы координат Х, x_2i *з относительно некоторой инерциальной системы координат (например, декартовой х_ИУ у_и, z"). Если R (f) — радиус-вектор начала координат системы Х, х₂, х₃, а П (г) — вектор угловой скорости вращения этой системы относительно инерциальной системы координат х_к, Уи'²и (рис. 5.20), ТО.

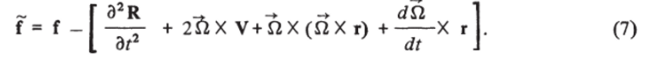
Здесь г — радиус-вектор рассматриваемой точки в системе координат х1 — х₃; V — вектор относительной скорости, компоненты которого.

tfi — и₃ являются искомыми функциями в уравнениях (1.9), f = J.

/₃). Выражения для /о, Л,. .. ,/4 остаются прежними, определяемыми соотношениями (1.11).

В принятой здесь, следуя [148], связи между неинерциальной и инерциальной системами координат через R (/) и П (г) имеем также.

где У* — скорость набегающего потока газа в инерциальной системе координат.

В задаче о продольных колебаниях затупленных тел в сверхзвуковом потоке газа (задача с осевой симметрией).

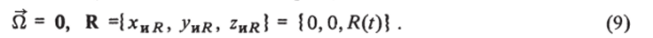
В частности, в сферической системе координат (1.12) для продольных гармонических колебаний затупленных тел с амплитудой А/oj и частотой со = 2тг/Г имеем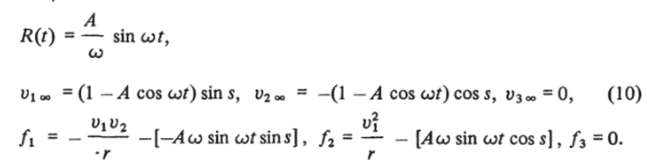

Давление, плотность, энтальпия и скорость в набегающем потоке, а также обезразмеривание газодинамических функций определяются соотношениями (1), (2), в которых Моо = М₀ — теперь некоторое среднее значение за период (безразмерный) колебаний Т

В описанной постановке рассматривались продольные гармонические колебания сферы и цилиндрического торца, а также соответствующие колебания потока относительно тела, движущегося со сверхзвуковой скоростью V₀ = const [139]. Характерными параметрами задачи являются радиус сферы или цилиндра, плотность газа в набегающем потоке и среднее значение V₀, относительно которого совершаются колебания. Основные расчеты проведены для средних значений чисел Маха М₀ = 10 и 2, А =0,31 и различных Т. Проведена также серия методических расчетов, в которых варьировались параметры разностной сетки, показавшие практическую сходимость результатов при h_x = As s я/20-гя/40 и h₂ = Аг- = 0,1 -i-0,05.

На рис. 5.21 для s = 0 (сплошные кривые) и s = я/4 (штриховые линии) представлены в зависимости от временит (за один период колебаний) давления на теле р₀ и на ударной волне р при обтекании колеблющейся сферы. По отмеченной сверху относительной скорости потока и сферы, которая равна 1 — A cos сot> можно судить о режиме движения. Отнесенное к периоду колебаний сферы нормализованное время г выбрано так, что при т = 0 тело неподвижно, поток движется с Моо (0 = 10; затем происходит уменьшение скорости потока относительно тела до минимального значения при т = 0,25 (тело ускоряется в направлении потока так, что (0 = = 6,6 при т — 0,25). На этом участке давление на теле уменьшается и остается меньше его величины на ударной волне, т. е. имеет место разрежение вблизи поверхности тела. При 0,25 < т < 0,5 тело тормозится относительно потока, давление на его поверхности возрастает.

В точке г = 0,5 скорость тела меняет знак и достигает максимума при г = 0,75, а скорость потока относительно тела при этом соответственно возрастает до Моо (/) = 13,1. Если тело при разгоне навстречу потоку достигает местной сверхзвуковой скорости (а в данном случае это имеет место), волна сжатия, появившаяся на поверхности тела при его разгоне, переходит в ударную волну, распространяющуюся по ударному слою и вскоре достигающую головную ударную волну, давление на которой резко возрастает. Затем слабая волна разгрузки, отразившись от головного скачка, достигает тела. Наблюдаемый при т = 0,75 второй максимум давления соответствует минимальному отходу и наибольшей скорости потока относительно тела. Из приведенных на рис. 5.21 штриховых линий следует, что вниз по потоку (s = я/4) отмеченные эффекты уменьшаются.

На рис. 5.22 для сферы показано изменение давления на оси симметрии от ударной волны (т? = 1) до точки торможения (г? = 0) в разные моменты времени. Здесь можно проследить формирование внутренней ударной волны и ее перемещение в сторону головного скачка уплотнения, который, в свою очередь, движется ей навстречу вследствие увеличения числа Маха относительного движения потока и тела и связанного с этим уменьшения величины отхода.

Следует отметить, что в рассмотренном случае головная ударная волна испытывает значительные деформации наряду с изменением отхода. Если,.

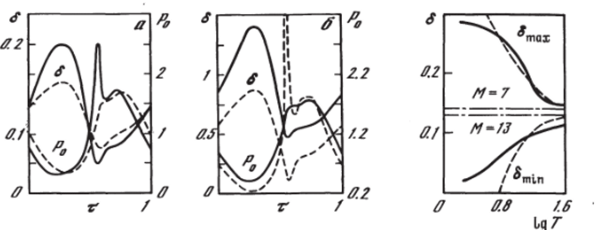
Рис. 5.23.

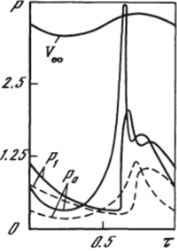
Рис. 5.21.

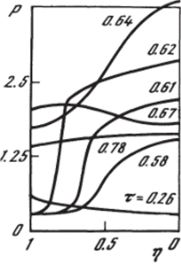
Рис. 5.22.

Рис. 5.24

например, отношение величины отхода при s = я/ 2 к его значению на оси симметрии равно ~ 3 для г = 0, то при т = 0,6 это отношение возрастает почти на порядок.

При М₀ = 10, Г = 4 проводилось сопоставление расчетов колебаний потока и тела. На рис. 5.23д представлены зависимости от времени давления в точке торможения колеблющегося торца р₀ и величины отхода ударной волны 5 (сплошные линии) и проведено сравнение этих величин с результатами решения задачи о колебаниях набегающего потока (штриховые линии). Как видно, различие получается существенным, что объясняется ролью инерциальных членов в правых частях системы (1.9).

В аналогичных расчетах при М₀ = 2 также наблюдается повышение давления и распространение волны сжатия, однако при данных значениях амплитуды и частоты колебаний скорость газа оставалась дозвуковой в ударном слое вблизи оси симметрии, поэтому внутренние ударные волны здесь не наблюдались.

Помимо сферы рассматривалось обтекание колеблющегося цилиндрического торца. На рис. 5.23, б для сферы представлены зависимости от времени величины отхода волны 5 и давления в точке торможения р₀ на оси симметрии для двух вариантов: 1 — М₀ = 2, Т= 20 (сплошные кривые) и 2 — М₀ =10, Г = 10 (штриховые линии). Основное отличие от обтекания сферы состоит в том, что нелинейные эффекты проявляются здесь значительно сильнее. В отличие от приведенных на рис. 5.23, б результатов параметры течения около сферы для случая 1 близки к гармоническим, имеется один максимум давления. В условиях 2 пик давления на поверхности сферы только лишь намечается, величина его от стационарного значения отличается примерно на 2%.

Согласно линейной теории, при гармонических колебаниях тел все искомые функции являются гармоническими и их можно представить в виде.

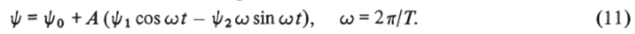
Параметр со обычно называют числом Струхаля. В выражении (11) ф₀ — решение нелинейной стационарной задачи: i//i, ф₂ — не зависящие от времени аэродинамические производные, которые находятся из решения линеаризованных уравнений. Сравнение в широком диапазоне чисел Струхаля данных линейной и нелинейной теории для случая колебаний сферы с амплитудой А =0,31 показано на рис. 5.24. Сплошными линиями отмечены наибольшие 5_тах и наименьшие 5_mj_n значения отхода волны при s = 0, полученные на основе нелинейных уравнений; штриховыми — соответствующие величины для линейной теории, выражения для которых можно получить из соотношения (11), приравняв нулю производную по времени. После преобразований получаются формулы для вычисления максимального (знак плюс) и минимального (минус перед радикалом) значений параметров газа:

Функции ф и ф2 при s = 0 взяты из работ [145, 146]. Штрихпунктирные линии на рис. 5.24 соответствуют стационарному обтеканию сферы при Моо = 7 и М_ж = 13 и нанесены для ifpoeepKH гипотезы квазистационарности. Как видно из рис. 5.24, даже при колебаниях с большими амплитудами результаты линейной и нелинейной теорий хорошо согласуются при больших Т (малые числа Струхаля). Для исследования неустановившихся течений, характерное время нестационарного процесса которых одного порядка с характерным временем течения (Г~ 1), необходимо использовать нелинейный подход.

В работах [149, 150] с использованием описанного выше алгоритма рассмотрен ряд других нестационарных задач в нелинейной постановке.

4. В заключение этого раздела рассмотрим примеры сверхзвукового обтекания затупленных тел с учетом интенсивного (в том числе пространственного и нестационарного) вдува в ударный слой газа того же состава, что и в набегающем потоке [57, 151]. Из других работ, в которых также в постановке невязкого, нетеплопроводного газа численно исследуются задачи со вдувом, отметим, например, [152, 153] (осесимметричные стационарные задачи) и [154, 155] (пространственные стационарные задачи). Постановка этих задач описана в разд. 1, при этом на участке поверхности тела со вдувом использовались граничные условия как для ''естественного" вдува типа (1.22), (1.24)-(1.26), так и для ''принудительного" вдува (1.24), (1.28). Некоторые результаты расчетов представлены на рис. 5.25-5.32.

Как известно, в зависимости от величины к = p_Wo К^_о/р" (отношение скоростных напоров вдуваемого и набегающего потоков) или другого характеризующего интенсивность вдува параметра реализуется либо.

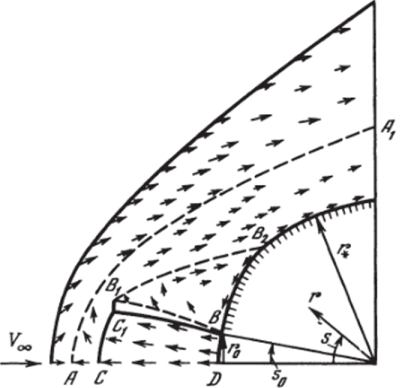
Рис. 5.25 Рис. 5.26

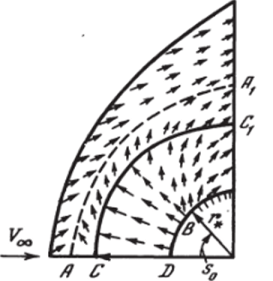
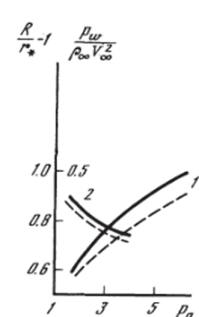
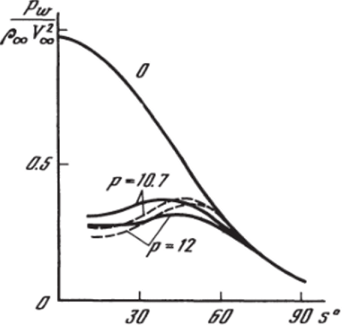
Рис. 5.27 Рис. 5.28

простейшая картина обтекания с головной ударной волной и контактным разрывом, соответствующая умеренным значениям к, либо значительно более сложная схема обтекания с системой внутренних скачков уплотнения СС|, СВ, СВ и застойной областью возвратного течения ВВ_ХВ₂ (рис. 5.25) или интенсивной внутренней ударной волной СС_Х (рис. 5.26). В пространственных задачах, а также при нестационарном вдуве возможно дальнейшее усложнение картины обтекания, ее перестройка со временем (например, замыкание контактного разрыва на поверхности тела и др.). Использование подходов, связанных с выделением всех особенностей течения (поверхностей разрывов), становится практически не реализуемой задачей. Методы сквозного счета (с использованием обычно консервативных схем) в таких случаях требуют слишком подробных сеток для приемлемого разрешения деталей течения, что также довольно трудно обеспечить, особенно в пространственных задачах. В связи с этим представляют определенный интерес подходы, связанные с явным выде;

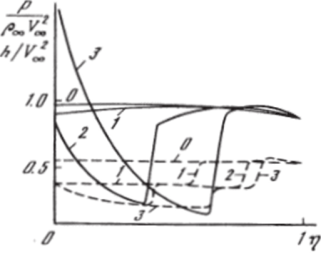
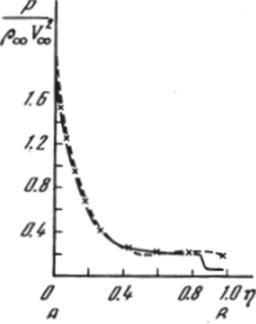
Рис. 5.29 Рис. 5.31

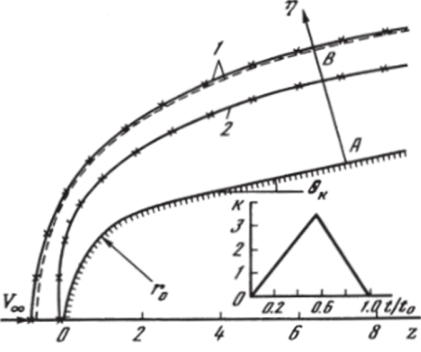
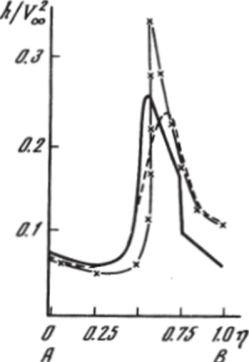
Рис. 5.30 Рис. 5.32

лением лишь основных особенностей течения (головной ударной волны и, быть может, контактного разрыва) и сквозным расчетом остальных поверхностей разрыва.

Представленные здесь расчеты проводились с явным выделением головной ударной волны и контактного разрыва, а также только головной ударной волны с использованием недивергентного варианта схемы 1, т. е. (4.4.4), а в модельном одномерном случае без выделения всех поверхностей разрыва с использованием консервативного варианта этой схемы, т. е. (4.2.11). Использование недивергентных схем для расчета разрывных решений требует известной осторожности, поэтому одной из целей этих расчетов, имеющих, естественно, и самостоятельный интерес, было определение возможностей схемы (4.4.4) для расчета таких достаточно сложных течений.

На рис. 5.25 представлена наблюдаемая в эксперименте [156] схема осесимметричного сверхзвукового обтекания сферы радиуса г., из передней части которой на участке BD (из сопла радиусом г₀) в ударный слой вдувается струя газа того же состава, что и в набегающем потоке (к = 1.4), а также полученное в расчетах с выделением только головной ударной волны поле скоростей (стрелки). Число Маха набегающего потока = 2,5, число Маха на срезе сопла М₀ = 1,5, отношение давлений на срезе, сопла и в набегающем потоке р = Ро1р_ж = 20 отношение r_#/r₀ = d = 5.

На рис. 5.27 с экспериментальными данными 1156] для различных условий обтекания (штриховые линии) сравниваются результаты численного решения (сплошные кривые) для отхода ударной волны на оси симметрии течения б = R_c/r, — 1 (кривые 1) и давления на теле в застойной зоне ВВ2 (кривые 2). Аналогичные сравнения по распределению давления на поверхности сферы приведены на рис. 5.28 для двух режимов вдува (р = 10,7 и 12). Кривая 0 на этом рисунке соответствует обтеканию сферы без вдува. Расчеты выполнены В. С. Финченко и И. А. Козловым. Видно, что численное решение удовлетворительно воспроизводит основные особенности таких решений не только качественно, но и количественно по ряду важных с практической точки зрения параметров (размеры области возвратного течения и положение точки присоединения В₂, давление в застойной зоне, отход головной ударной волны и др.).

На рис. 5.26 показана установившаяся картина обтекания сферы и поле скоростей, полученных из численного решения в аналогичной же постановке для случая еще более высоких значений параметра вдува к, когда вдуваемая в ударный слой по нормали к поверхности тела на участке DB струя является сильно недорасширенной. Приведенные на рис. 5.29 распределения вдоль оси симметрии течения от тела (т? = 0) до головной ударной волны (rj = 1) давления р1р_ж У²_Ж (сплошные кривые) и энтальпии h/V²^ (штриховые линии) показывают динамику формирования и развития этой картины обтекания с ростом во времени (нестационарный вдув) параметра к от нуля (кривые 0) до значений к > 1 (кривые 2, 3). Умеренным значениям к ^ 1 соответствуют кривые 1.

Результаты расчета пространственного сверхзвукового обтекания затупленного по сфере конуса, с части поверхности которого г = R" (s, <�р), 5 > 0, 0 < я/2 (см. 1.12, рис. 5.1) по нормали к поверхности тела осуществляется неравномерный по s, нестационарный вдув, представлены на рис. 5.30−5.32 (штриховые линии). Расчеты проводились по недивергентной схеме (4.4.4) с явным выделением только головной ударной волны 1. Число Маха набегающего потока М_ж = 23, показатель адиабаты к = 1,4, зависимость от времени на образующей конуса = 0 параметра к показана на рис. 5.30 (зависимость от у косинусоидальная). Здесь же представлены результаты расчетов аналогичной осесимметричной задачи (к (<�р) — = к (0) = const) с использованием той же схемы, но с дополнительным явным выделением контактного разрыва 2 (кривые с крестиками), а также результаты расчета по консервативной схеме (4.2.11) одномерной задачи, моделирующие трехмерное течение на боковой образующей конуса у = 0 вдоль АВ (сплошные кривые). В_% последнем случае все разрывы, включая головную ударную волну, рассчитывались сквозным образом. На рис. 5.30 показана картина обтекания в плоскости симметрии течения.

= 0 (см. также рис. 5.1), на рис. 5.31 и 5.32 приведены профили давления р!р_ж У²_Ж (рис. 5.31) и энтальпии h/У²^ (рис. 5.32) вдоль луча АВ.

Проведенные сопоставления показывают, что численное решение этой задачи с использованием разных постановок и разностных схем дают достаточно близкие результаты. Заметные отличия наблюдаются лишь в величине энтальпии вблизи контактного разрыва вне затупления, где последняя имеет острый пик, смазываемый при сквозном расчете контактного разрыва.

Заключая данный раздел, отметим, что приведенные здесь и в других работах примеры показывают достаточно высокую эффективность сеточно-характеристических методов (в том числе недивергентных схем первого порядка точности) для численного решения разнообразных сложных задач газовой динамики при выборе рациональных постановок этих задач.