Шумоподобные сигналы. 
Теория электросвязи

Важными достижениями в XX в. явились создание шумоподобных или широкополосных сигналов и разработка на их основе новых систем связи. Поэтому теперь переносчиком (несущим колебанием) информации стал не только гармонический, импульсный, цифровой, но и сложный широкополосный сигнал.

Шумоподобпый сигнал (ШПС) — аналоговый сигнал, содержащий много гармонических составляющих в выбранной полосе частот. Шумоподобные сигналы создаются благодаря дополнительной модуляции несущих колебаний по псевдослучайному закону. За счет дополнительной манипуляции несущей амплитудно-частотный и энергетический спектры сигнала расширяются. Функция корреляции сигнала приобретает узкий выброс. Шумоподобные сигналы с фазовой манипуляцией используются для разделения лучей при многолучевом распространении радиоволн в системах связи и радионавигации, для подавления сосредоточенных помех и построения систем скрытой связи. Особое свойство ШПС заключается в том, что они относятся к классу сложных сигналов, база которых В_с = 2F_c тс «1 (обычно В = 100^-10 000). Так, в системах связи стандарта CDMA, использующих ШПС, поступающие на вход приемника помехи подавляются в В = W/Fраз. Это свойство ШПС позволяет многократно и одновременно использовать один частотный канал для связи разных абонентов.

Идеи построения ШПС были связаны с частотной модуляцией несущей частоты вспомогательным сигналом, структура которого должна была быть известна на приеме. В 1942 г. был изобретен способ формирования ШПС методом скачкообразного изменения частоты несущего колебания за время передачи одного информационного символа (frequency hopping spread spectrum — FH-SS). Также ШПС формируют методом скачкообразного изменения относительного временного положения коротких кодовых импульсов за время передачи одного информационного символа (time hopping spread spectrum — TH-SS). Широко применяемым способом формирования ШПС является метод прямого расширения спектра путем непосредственной фазовой модуляции несущей кодовой последовательностью (direct sequence spread spectrum — DS-SS).

В отмеченных случаях возможно создание в общей полосе частот больших ансамблей сигналов, которые отличаются либо законом чередования фазы несущего колебания для сигналов DS-SS, либо законом изменения несущей частоты для сигналов FH-SS, либо определенной временной расстановкой коротких импульсов для сигналов TH-SS.

Расширенный спектр {spread spectrum — SS). Предположим, что создан узкополосный сигнал, промодулированный потоком данных с заданной скоростью. Пусть есть повторяющаяся псевдослучайная цифровая последовательность со значительно большей скоростью. Меняя фазу узкополосного сигнала в соответствии с псевдослучайной последовательностью, получим ШПС с широким спектром, содержащим передаваемую информацию. Если рассмотреть, что происходит с точки зрения частоты, то получится, что полезный сигнал «расплылся» {spread) но спектру. Принятый и демодулированный сигнал перемножим с копией ШПС, который использовали для модуляции, и получим узкополосную составляющую с высокой энергией на единицу частоты — переданный поток данных. Поскольку помехи и сигналы от других передатчиков не совпадают с используемым ШПС, то после перемножения они еще больше расползутся по спектру и их энергия на единицу частоты уменьшится. Таким образом, используя разные псевдослучайные последовательности, можно организовать несколько независимых каналов передачи данных в одной и той же полосе частот.

Эффект первый. При перемещении точки приема эти условия периодически изменяются, так как сложение волн, приходящих с разных направлений, создает пространственную интерференционную картину. Эффект особенно сильно сказывается на мобильных пользователях и типичен для узкополосных систем. Для систем с SS действие эффекта ослабляется, поскольку на разных частотах в пределах его широкого спектра создаются разные интерференционные картины, что выравнивает результирующий сигнал.

Эффект второй. Время задержки сигналов при прохождении больших расстояний может меняться из-за изменений характеристик среды распространения, причем это сказывается по-разному на сигналах, приходящих разными путями, что при сложении вызывает временные флуктуации уровня сигнала, называемые в радиосвязи замираниями. Несинфазное изменение уровня сигнала на разных частотах спектра SS сигнала приводит к сильному ослаблению действия этого эффекта на подобные системы.

Отметим еще две (кроме полосы) особенности шумоподобного сигнала:

• • при формировании используется фактор псевдослучайности, благодаря чему по своей структуре он становится близким к случайному сигналу;
• • распознать его при приеме можно, зная ключ кодирования при передаче, что обеспечивает скрытность связи. Это реализуется «размазыванием» передаваемого сигнала по спектру и требованием, чтобы приемник «знал», как его «собирать».

В настоящее время в теории информации разрабатывают методы синтеза сигналов с заданными автокорреляционными и спектральными свойствами. Если рассматривать последовательности из п импульсов прямоугольной формы, которые в соответствии с номером позиции М могут принимать значения ±1, то простым перебором можно найти последовательности, для которых.

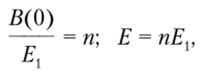
где В (0) — АКФ; Е — энергия всего сигнала; Е_{ — энергия одного элемента.

Наиболее распространенным примером технической реализации шумоподобных сигналов служат сформированные псевдослучайные последовательности прямоугольных радиоимпульсов длительностью т, в частности при манипуляции несущего колебания двоичными цифровыми кодами. База таких сигналов определяется числом модулирующих импульсов в исходной последовательности. Успешно развиваются методы передачи сигналов, созданные на основе ортогональных последовательностей в виде линейных рекуррентных М-последовательностей (таких как последовательности Голда, Лежандра и пр.), функций Радемахера, Уолша и др.

Линейные М-последовательности. Рассмотрим линейные рекуррентные М-последователыюсти. Для линейной М-последователыюсти отношение значения главного максимума к максимальному значению бокового лепестка АКФ растет как 4п, где п = 2^м — 1 — число импульсов в последовательности; ц — целое положительное число. Линейные рекуррентные последовательности обладают свойством хаотичности: если из периода следования такой последовательности, содержащей п членов, выбрать возможные отрезки по р членов в каждом, то:

• • среди этих отрезков не будет совпадающих;
• • среди них найдутся любые комбинации из +1 и -1, состоящие из р членов (кроме запрещенной комбинации, включающей только +1).

Эти свойства сходны со свойствами случайных разнополярных последовательностей, поэтому М-последовательности называют шумоподобными последовательностями. При передаче шумоподобных последовательностей по каналу связи обычно применяется фазовая или относительная фазовая модуляция.

Сигналы на основе функций Радемахера. Аналитическая интерпретация этих функций встречает определенные сложности, однако идея их построения сравнительно проста. Функции Радемахера образуются из синусоидальных функций с помощью соотношения.

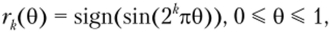
где 0 = t/T — безразмерное время; Т — период; k = 0,1, 2,… — порядок функции.

Функции Радемахера, принимающие значения ±1, можно трактовать как функции «прямоугольного синуса» («прямоугольной волны»), и они имеют форму меандра. На рис. 3.25 показаны временные диаграммы первых четырех функций Радемахера. Нетрудно заметить, что функции Радемахера г (0) ортонормированы на интервале 0 < 0 < 1:

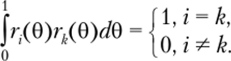
Шумоиодобные сигналы на основе функций Уолша. Дальнейшим развитием систем функций типа последовательностей Радемахера, имеющих форму «прямоугольной волны», стала ортонормированная система функций УолшаГ Широко используемые в теории связи функции Уолша — одни из немногих ортонормированных функций, которые на отрезке существования (периоде следования (-7/2, Т/2)) принимают два значения: +1 или -1.^[1]

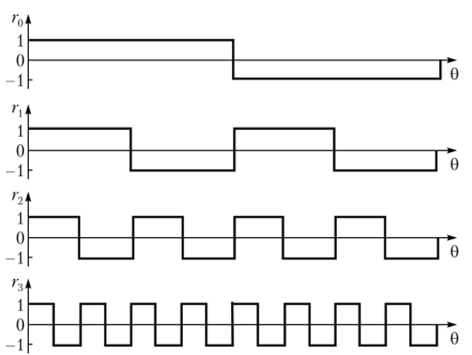
Рис. 3.25. Временные диаграммы первых четырех функций Радемахера.

Введем безразмерное время, нормированное к периоду следования: 0 = t/T, и обозначим k-ю (к — порядок) функцию Уолша символом wal (&, 0). Идею построения последовательностей Уолша можно уяснить из рис. 3.26, где показаны первые восемь этих функций. Ортонормированность функций следует из принципа их построения и может быть проверена непосредственно путем вычисления интеграла. Система wal (?, 0) позволяет продемонстрировать наиболее важные свойства функций Уолша, определяемые рекуррентным уравнением.

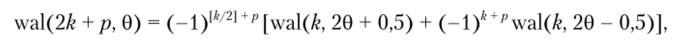
где обозначение [к/2] представляет собой наибольшее целое число, меньшее или равное k/2; параметр р может принимать только два значения: 1 или 0. Функции Уолша нормированы к единице при любом порядке к: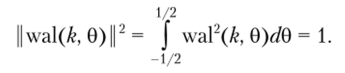

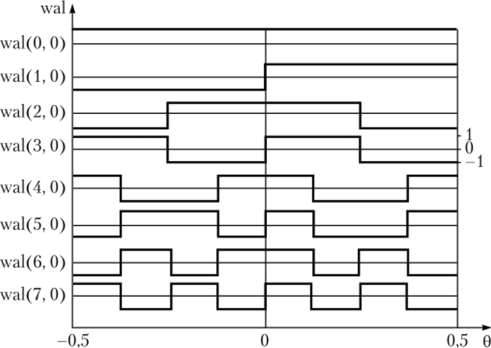
Рис. 3.26. Восемь первых функций Уолша.

При перемножении двух функций Уолша получается также функция Уолша (свойство мультипликативности):

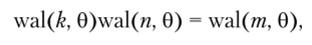
где т — порядок функции — является суммой порядков к и п по модулю 2 (обозначается т = k ® п).

Модульное сложение двух цифр по модулю h отличается от привычного тем, что полученная сумма приводит к числу, большему h — 1. Из обычной суммы при модульном сложении вычитается число h. При сложении двух цифр по модулю 10, например, получим 8 © 7 = 5 (mod 10); при сложении цифр по модулю 2 находим 1 © 0 = 1 (mod 2), по 1 © 1 = 0 (mod 2) и т. д. Чтобы проделать такое сложение для функций Уолша, следует представить числа Ь: ив двоичной форме и сложить их без переносов в старшие разряды согласно следующим правилам: 1(c)0 = 1;0(c)1 = 1;0(c)0 = 0;1(c)1 = 0.

Умножение функции Уолша самой на себя дает функцию нулевого порядка, так как результатом являются произведения вида (+1)(+1) и (-1)(-1):

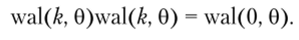
Также нетрудно показать, что умножение функции любого порядка wal (&, 0) на функцию нулевого порядка wal (0, 0) оставляет первую без изменения:

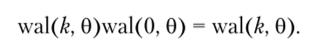
На рис. 3.26 можно заметить, что четным относительно середины интервала определения (0 = 0) функциям wal (&, 0) соответствуют четные номера k, а нечетным функциям — нечетные номера. Такое взаимно однозначное соответствие между четностью функций wal (&, 0) и четностью их номера к

аналогично свойствам гармонических функци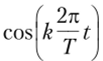й и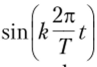

В ряде случаев используются обозначения са1(&, 0) для четных функций и sal (&, 0) для нечетных функций Уолша. Эти функции связаны соотношениями.

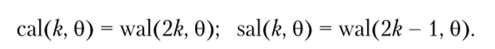
Способ нумерации функций Уолша называется упорядочением. Разработаны и существуют несколько принципов упорядочения функций Уолша. Функции Уолша, показанные на рис. 3.26, упорядочены по Уолшу. Часто применяются системы функций Уолша, упорядоченные по Адамару (Hadamard) [had (/?, 0)| и по Пэли (Peley) |ра1(ф, 6)|. Упорядочение по Уолшу характерно тем, что номер k функции wal (&, 0) равен числу перемен знака на интервале ее существования.

Функции Уолша формируют с помощью матриц Адамара. Матрицей Адамара H_N порядка N = 2″ называется квадратная матрица размера N х N с элементами ±1, такая что функция Уолша, упорядоченная по Адамару |had («, Т) с номером и], является последовательностью прямоугольных импульсов с единичными амплитудами и полярностями, соответствующими знакам п-й строки матрицы, и определенными длительностями этих импульсов. Под длительностью прямоугольных импульсов подразумевают.

1/iV-io долю интервала ортогональности [0, 7], или, при введении безразмерного времени (интервала), — [0, 1].

Для примера на рис. 3.27 представлены восьмая функция Уолша, упорядоченная, но Адамару, и ее АКФ. Очевидно, что за счет корреляционной обработки выходной сигнал значительно превышает по уровню амплитуду исходной последовательности. По рассмотренной системе базисных функций Уолша интегрируемую на интервале ()<()<] функцию ц (0) можно представить рядом Фурье.

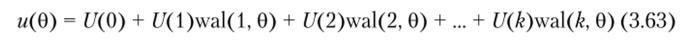
с коэффициентами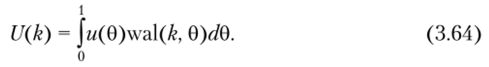

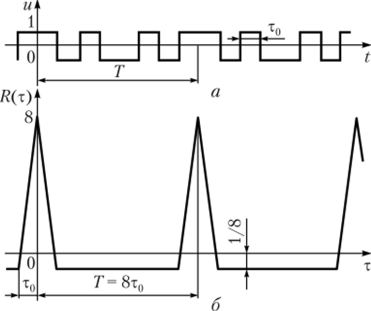
Рис. 3.27. Функция Уолша, упорядоченная по Адамару:

а — диаграмма восьмой функции; б — АКФ Пример 3.7.

Задан сигнал в форме прямоугольного треугольника с единичной амплитудой и длительностью т_и (рис. 3.28, а). Вычислим два первых коэффициента разложения сигнала в ряд Фурье по ортонормированной системе функций Уолша и аппроксимируем ими заданный сигнал.

Решение

На интервале времени [-т_и/2, т_н/2] заданный треугольный импульс аналитически описывается функцией вида u (t) = t/т_и + 1/3.

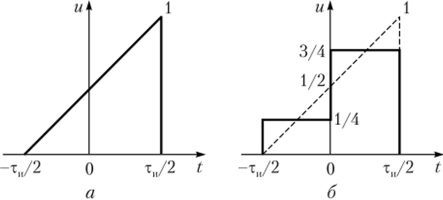
Рис. 3.28. Разложение треугольного сигнала, но функциям Уолша:

а — исходный сигнал; 6 — две аппроксимирующие функции Вычислим коэффициенты с_к обобщенного ряда Фурье по формуле (2.10):

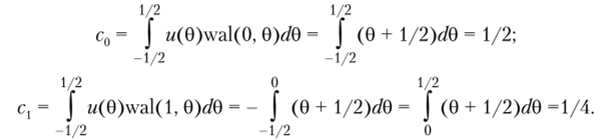
В результате представления заданного сигнала двумя первыми членами по ортонормированной системе функций Уолша получена приближенная аппроксимация ступенчатой формы (рис. 3.28, б). Увеличение суммируемых членов ряда Фурье приведет к повышению точности аппроксимации.

Пример 3.8.

На интервале разложения Т_п определим спектр отрезка синусоиды единичной амплитуды и{1) = sin| (2тт/)/7'| (рис. 3.29) в базисе функций Уолша.

Решение

Интервал разложения Г_(| целесообразно приравнять периоду синусоиды Т. Как это принято в теории функций Уолша, перейдем к безразмерному времени 0 = t/Tи запишем исходное колебание и (Г) в форме н,(0) = sin (2rc0). Для сокращения выкладок ограничимся 16 функциями, причем сначала выберем упорядочение по Уолшу.

Поскольку заданная функция м,(0) нечетна относительно 0 = ½, то все коэффициенты U (k) при четных функциях Уолша в ряде (3.63), т. е. при са1(/л 0), равны нулю. Остальные восемь функций wal (&, 0), которые совпадают с функ;

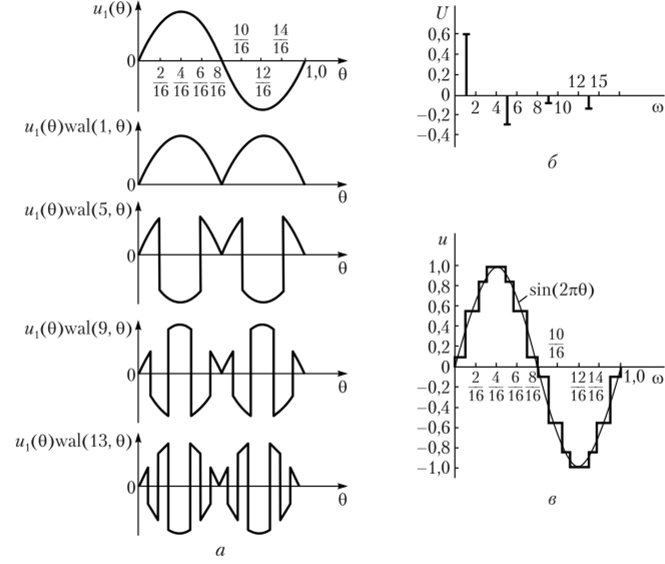
Рис. 3.29. К определению спектра отрезка синусоиды единичной амплитуды:

а — перемножение отрезка синусоиды и функций Уолша; б — спектр; в — восстановление исходного сигнала циями Радемахера и имеют периодичность внутри интервала [0, 1], кратную периоду функции Wj (0), также приводят к нулевым коэффициентам U (k). К таким функциям относят wal (3, 0), wal (7, 0) и wal (15, 0). Функция wal (ll, 0), нечетная не только относительно точки 0 = ½, а также относительно точек 0=¼ и 0 = ¾ (внутри интервалов [0, ½] и [½, 1]), имеет нулевой коэффициент [/(11) из-за четности м,(0) в указанных интервалах. Таким образом получено, что лишь четыре коэффициента из 16 не равны нулю: [/(1), [/(5), [/(9) и [/(13). Определим эти коэффициенты по формуле (3.64). Подынтегральные функции Wj (0)wal (A, 0), являющиеся произведениями исследуемого сигнала и соответствующей функции Уолша, показаны на рис. 3.29, а. В результате интегрирования этих произведений находим:

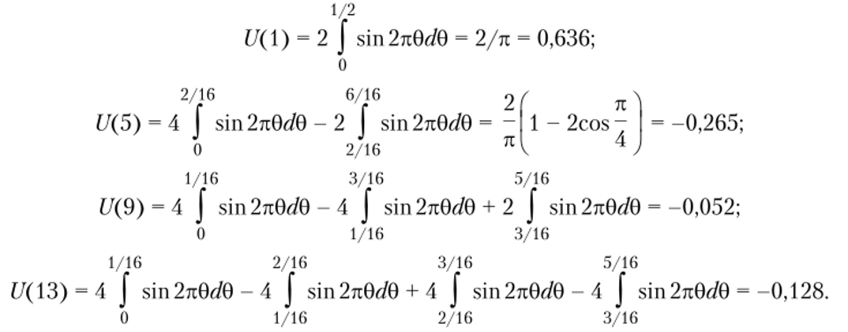
Спектр исследуемого сигнала и,(0) в базисе функций Уолша показан на рис. 3.29, 6. Восстановление исходного сигнала (см. рис. 3.29, а) 16 функциями Уолша показано па рис. 3.29, в (12 спектральных коэффициентов обращаются в нуль). Очевидно, что для более удовлетворительной аппроксимации синусоидального колебания в базисе Уолша требуется существенное увеличение числа спектральных компонентов.

• [1] Джозеф Леонард Уолш (J. L. Walsh, 1895—1973) — американский математик.