Теорема Котельникова (теорема отсчетов)
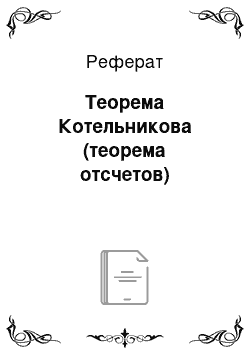
Представление сигнала u (t) рядом Котельникова (6.3) иллюстрируется диаграммами на рис. 6.4. На графике построены четыре первых члена ряда, соответствующие отсчетам сигнала в моменты 0, At, 2At и ЗД?, взятым в соответствии с теоремой Котельникова. При суммировании этих членов ряда в любые отсчетные моменты kAt непрерывный сигнал абсолютно точно восстанавливается независимо от числа выбранных… Читать ещё >
Теорема Котельникова (теорема отсчетов) (реферат, курсовая, диплом, контрольная)
Проблема дискретизации сигналов с ограниченным спектром широко освещена в литературе, и основой ее служит теорема Котельникова (теорема Найквиста — Шеннона, или теорема отсчетов). Считается, что первыми фундаментальными трудами в этой области были работа В. А. Котельникова «О пропускной способности „эфира“ и проволоки в электросвязи» (1933) и статья К. Шеннона «Связь при наличии шума» (1949). Статья К. Шеннона была написана на основе работы Е. Т. Уттакера «Функции, представляемые распространением теории интерполяции» (1915). Проблема представления функции отдельными значениями и восстановления ее при помощи интерполяции начала решаться в XVIII в. в работах О. Коши, П.-С. Лапласа и т. д., а позднее описана повторно Д. Карсоном и Р. Хартли.
Для того чтобы восстановить исходный непрерывный сигнал из дискретизированного с малыми погрешностями, необходимо рационально выбрать шаг дискретизации. Поэтому при преобразовании аналогового сигнала в дискретный обязательно возникает вопрос о величине шага дискретизации At. Интуитивно нетрудно понять следующую разумную идею. Если аналоговый сигнал обладает низкочастотным спектром, ограниченным некоторой верхней частотой FB (т.е. функция u (t) имеет вид плавно изменяющейся кривой без резких изменений амплитуды), то вряд ли на некотором небольшом временном интервале дискретизации At эта функция может существенно изменяться, но амплитуде.
Точность восстановления аналогового сигнала по его отсчетам зависит от интервала дискретизации At. Чем он короче, тем меньше будет отличаться функция u (t) от кривой, проходящей через точки отсчетов. Однако с уменьшением интервала At существенно возрастают сложность и объем обрабатывающей аппаратуры. При большом интервале дискретизации At возрастает вероятность искажения или потери информации при восстановлении аналогового сигнала.
Оптимальное значение интервала дискретизации устанавливается теоремой Котельникова. Согласно одной из наиболее известных и простых интерпретаций этой теоремы произвольный сигнал u (t), спектр которого ограничен некоторой частотой FB, может быть полностью восстановлен по последовательности своих отсчетных значений, следующих с интервалом времени

Интервал дискретизации At и частоту Fd = Fn в теории связи иногда называют соответственно интервалом и частотой Найквиста.
Аналитически теорема Котельникова представляется рядом.
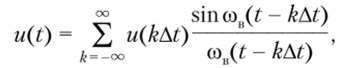
где k — номер отсчета; u (kAt) — значения непрерывного сигнала u (t) в точках отсчета; сов = 2nFn = к/At — верхняя частота спектра сигнала.
Для доказательства теоремы рассмотрим аналоговый сигнал u (f), спектральная плотность 5(со) которого сосредоточена в полосеоов < со < соп (сплошная линия на рис. 6.2). Дополним график спектральной плотности симметрично значениям, повторяющимся с периодом 2сов (штриховые линии на рис. 6.2). Полученную периодическую функцию разложим в ряд Фурье, заменив в формуле (2.20) аргумент t на со, частоту cot = сов на At и п на k. Тогда.

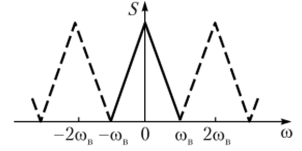
Рис. 6.2. Представление спектральной плотности периодической функцией
Полагая в формуле (2.21) период 2сов, а интервал дискретизации At = л/соп, получим.
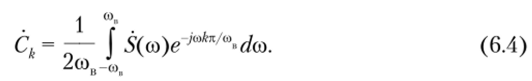
Используя обратное преобразование Фурье (2.30), запишем сигнал как.
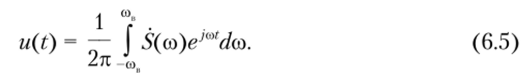
Таким же образом запишем значение дискретизированного сигнала для некоторого k-vo отсчета времени. Поскольку t = kAt = kn/сов, то.
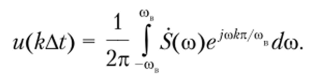
Сравнив эту формулу с формулой (6.4), замечаем, что Ck = Atu (kAt). С учетом этого соотношения спектральная функция (6.3) после преобразований примет вид.
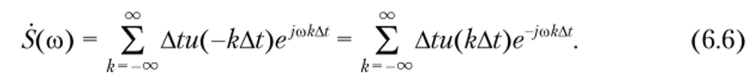
Подставим соотношение (6.6) в формулу (6.5), изменим порядок интегрирования и суммирования, представим n/At = <�ов и вычислим интеграл. В результате получим.
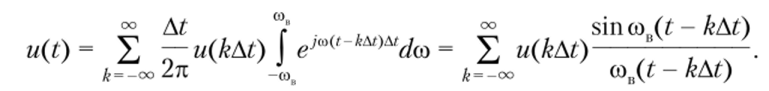
Из этой формулы следует, что непрерывная функция u (t) действительно определяется совокупностью ее дискретных значений амплитуды в отсчетные моменты времени t = kAt, что и доказывает теорему Котельникова. Сигналы.
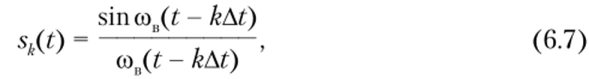
ортогональные на интервале [-°°, +°°], называются функциями отсчетов или функциями Котельникова. График k- функции Котельникова представлен на рис. 6.3. Каждая из функций sk(t) сдвинута относительно ближайшей sk ,(?) или sk + l(t) на интервал дискретизации At. Анализ формулы.
(6.7) и графика на рис. 6.3 показывает, что сигнал sk(t) отражается функцией sinx/xy которая характеризует огибающую спектральной плотности прямоугольного импульса.
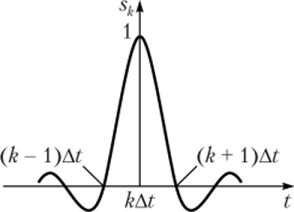
Рис. 6.3. График &-й функции Котельникова.
Представление сигнала u (t) рядом Котельникова (6.3) иллюстрируется диаграммами на рис. 6.4. На графике построены четыре первых члена ряда, соответствующие отсчетам сигнала в моменты 0, At, 2At и ЗД?, взятым в соответствии с теоремой Котельникова. При суммировании этих членов ряда в любые отсчетные моменты kAt непрерывный сигнал абсолютно точно восстанавливается независимо от числа выбранных отсчетов. В интервале же между любыми отсчетами сигнал u (t) восстанавливается тем точнее, чем больше суммируется членов ряда (6.3). Заметим, что соединить дискретные отсчеты сигнала на графике прямыми линиями было бы не совсем верно, так как при восстановлении непрерывного сигнала по дискретному используют более сложные интерполирующие функции.
На практике эта теорема имеет огромное значение. Например, большинство звуковых сигналов можно с некоторой степенью точности считать сигналами с ограниченным спектром. Их спектр лежит ниже 20 кГц. Это значит, что при дискретизации с частотой не менее 40 кГц мы можем потом более или менее точно восстановить исходный аналоговый звуковой сигнал по его цифровым отсчетам.
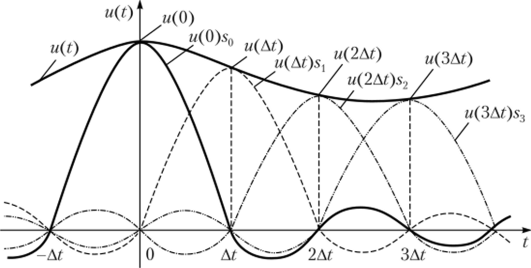
Рис. 6.4. Аппроксимация непрерывного сигнала рядом Котельникова.
Пример 6.1.
Сигнал звукового сопровождения в телевизионном канале ограничен верхней частотой /" = 12 кГц. Определим интервал At между отсчетами, необходимый для неискаженного воспроизведения дискретизированного сигнала. Решение
Определяем интервал дискретизации: At = 1/(2/в) = 1/(2 • 12 -10 ') ~ 42 • 10 6с.
Впоследствии было предложено много различных способов аппроксимации сигналов с ограниченным спектром, обобщающих теорему отсчетов:
- • для функций, отсчеты которых берутся в произвольные моменты времени;
- • для многомерных функций (например, для телевизионных сигналов);
- • для функций, у которых берутся отсчеты и самой функции, и ее производной.
Оценим возможность применения теоремы Котельникова к импульсному сигналу u (t) конечной длительности Тп. Такие сигналы теоретически обладают бесконечно широким спектром. Однако всегда можно ограничиться верхней частотой FB, за пределами которой в спектре содержится малая доля энергии по сравнению с энергией всего сигнала. В теории связи таким критерием является содержание 90% средней мощности сигнала в границах спектра. В этом случае сигнал u (t) длительностью ТИ с верхней граничной частотой спектра FB может быть представлен рядом Котельникова с ограниченным числом отсчетов.
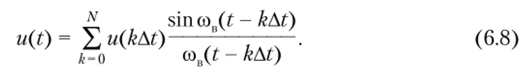
Здесь Лг = TJAt — число отсчетов.
Пример 6.2.
Представим рядом Котельникова прямоугольный импульс напряжения единичной амплитуды и длительности т" для двух случаев: спектр аппроксимирующей функции ограничен значениями верхней частоты FBl = 1/(2ти) и Fd2 = 1/т".
Решение
Для первого случая интервал дискретизации At = 1/(2FB) = ти, а значит, импульс будет представлен всего двумя отсчетными значениями — в начале и концс импульса. Подставив в формулу (6.8) значения амплитуды и длительности импульса, запишем математическую модель аппроксимирующей функции:
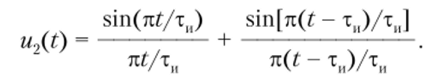
Во втором случае импульс дискретизируют тремя равными отсчетами, производимыми в моменты t = 0, т(1/2 и ти, т. е. в начале, середине и конце импульса. Тогда.
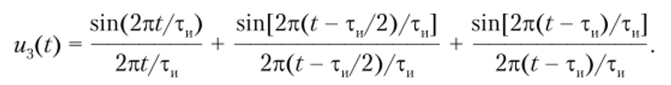
Временные диаграммы аппроксимирующих функций u2(t) и u3(t) и образующие их члены ряда Котельникова представлены на рис. 6.5.
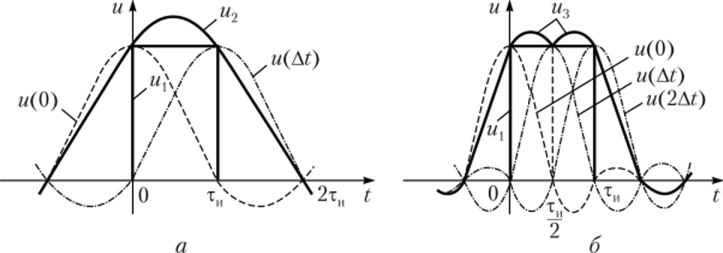
Рис. 6.5. Представление прямоугольного импульса отсчетами:
а — двумя; 6 — тремя Пример б. З Определим минимальную частоту дискретизации по Котельникову, при которой гармонический сигнал u (t) = cos (2nF0t + <�р0) может быть полностью восстановлен по своим отсчетным значениям (выборкам).
Решение
При выборе интервала дискретизации At = 1/(2FB), где FB — верхняя граничная частота спектра, непрерывный сигнал u (t) можно восстановить по отсчетам (рис. 6.6, а). Если соотношение частот F0 < FB, то к гармоническому сигналу применима теорема Котельникова. При этом отсчстные значения сигнала щ = = cos (knF0/FB + %).
В предельном случае, когда частота сигнала F0 стремится к частоте дискретизации FB слева, т. е. F0 = lim (Fn — р), на каждом периоде исходного сигнала долж;
м—о, но осуществляться два отсчета.
Восстановление функции зависит от фазы отсчетов сигнала относительно выборок. Если максимум синусоиды приходится на середину интервала между отсчетами, то погрешность наибольшая, если же на отсчет, то — наименьшая.
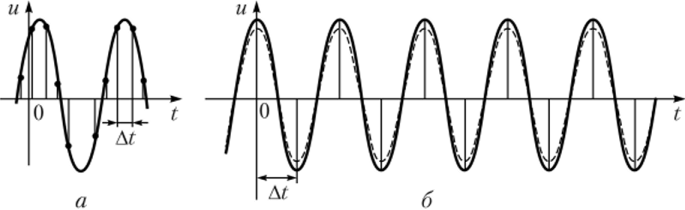
Рис. 6.6. Восстановление синусоиды:
а — при F0 < FB; 6 — по двум отсчетам Очевидно, что выборки могут попадать на нулевые значения синусоиды, экстремумы или промежуточные значения. Так как априорно фаза выборок относительно дискретизируемой синусоиды неизвестна, то после восстановления сигнала фильтром синусоиду можно не увидеть. В этом примере самая высокая точность восстановления синусоиды будет тогда, когда обе выборки взяты в ее максимальных значениях. Колебание на входе ФНЧ имеет пилообразную форму той же частоты, что и частота синусоиды (штриховые линии на рис. 6.6, б).
Если отсчеты производят недостаточно часто и условия теоремы Котельникова нарушаются, то однозначное восстановление гармонического сигнала невозможно. В этих случаях через отсчетные моменты времени можно провести бесчисленное множество кривых, спектральные плотности которых отличны от нуля вне полосы -Fn < F< Fn. Можно утверждать, что погрешность восстановления синусоиды при частоте выборок 2F0 может составлять 100%. Уже этого достаточно для подтверждения правильности изложенных выводов.
Пример 6.4.
Дискретизированный в соответствии с теоремой Котельникова непрерывный сигнал u (t) имеет два отсчета на временной оси (рис. 6.7). Вычислим мгновенное значение исходного сигнала в момент времени t = 1 мкс.
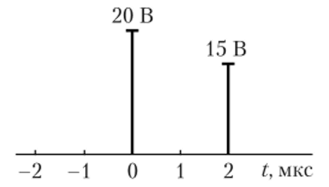
Рис. 6.7. График к примеру 6.4.
Решение
По рис. 6.7 определяем, что интервал дискретизации = 210 (,си верхняя частота спектра исходного сигнала сов = к/At = 1,57- 10f> с-1. Согласно формуле.
(6.8) ряд Котельникова в этом случае примет вид.
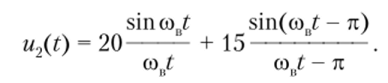
Из этого соотношения находим мгновенное значение аналогового сигнала в момент времени t = 1 мкс: u (t = 1 мкс) = 22,3 В.