Векторное пространство. 
Математическое моделирование

Выясним теперь, что можно сказать о тех множествах, между элементами которых отображение, А устанавливает соответствие. Рассмотрим плоскость. Выберем на ней некоторую точку, назовем ее нулем и обозначим знаком 0. После этого с любой точкой плоскости мы можем связать вектор (такой, каким его представляют в школе: направленным отрезком, стрелочкой, идущей из точки 0 в любую точку плоскости). Теперь множество точек плоскости можно трактовать как множество векторов, имеющих общее начало в точке 0. Эта трактовка есть, разумеется, не что иное, как взаимно однозначное отображение множества точек плоскости на множество компланарных векторов, выходящих из точки 0. Пусть две точки р и q лежат на одной прямой с точкой 0 (или, что-то же, два вектора р и q лежат на одной прямой). Допустим, каким-то образом мы умеем измерять длину. Обозначим длину вектора через /. Если l_pll_q = а, то будем говорить, что p = aq, когда р и q лежат по одну сторону от точки 0, и р — -aq, когда они лежат по разные стороны (рис. 27, а). Таким образом, мы определили умножение вектора на число. Далее, пусть р и q — два произвольных вектора. Определим их сумму г как вектор, направленный по диагонали параллелограмма, построенного на этих векторах. Длина этого вектора равна длине диагонали, т. е. г — р + q (рис. 27, б).

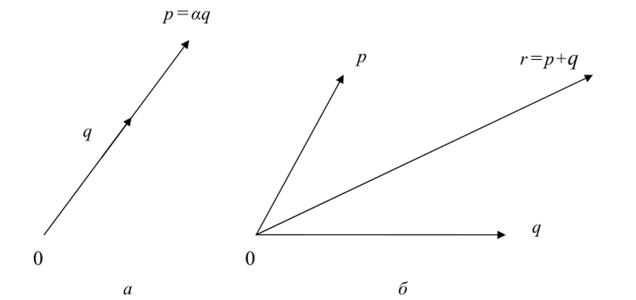
Рис. 27. Действия над векторами

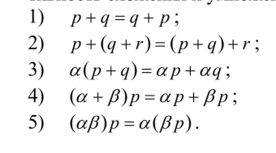
Необходимо понимать, что способы нахождения aq и p + q мы именно определили. Само по себе множество точек нс предполагает какого-либо способа определения aq и p + q. Мы можем (если в том возникнет потребность) определить эти операции иным способом и даже назвать по-другому (нет, опять же, никаких внутренних причин называть вектор г суммой, а не, скажем, произведением). То, как мы определили умножение на число и сумму, есть дань традиции и тем физическим соображениям, которые легли в основу этой традиции. Умножение на число и сумма векторов — примеры отображений, о которых говорилось выше. Первое отображает плоскость в себя: некоторая точка плоскости отображается в точку той же самой плоскости. Второе отображает любую пару векторов (элемент области определения есть любая пара векторов) в вектор: любой паре точек плоскости ставится в соответствие третья точка этой плоскости. Определенные нами отображения обладают рядом свойств. Во-первых, имеет место коммутативность и ассоциативность сложения и умножения на число:

Здесь а, р — числа, a p, q и г — векторы. Далее, точке 0, очевидно, соответствует нулевой вектор, для которого справедливо.

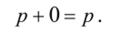
Кроме того, для любого вектора р существует вектор q, такой, что.

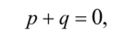
и он, естественно, обозначается через -р . И, наконец, если вектор р умножить на единицу, то он отобразится в себя (и длина, и направление останутся прежними). Множество, для элементов которого определено сложение и умножение на число, обладающее указанными свойствами, называется векторным пространством. Замечательным оказывается то, что вектором, т. е. элементом векторного пространства, может быть не только точка плоскости, а объект любой природы (как мы увидим далее — число, функция, оператор и прочее). Необходимо лишь определить сложение и умножение на число, обладающие указанными выше свойствами. Формализуем все вышесказанное следующим образом. Пусть V — некоторое непустое множество и /, g, h — некоторые его элементы. Это множество называется векторным (или линейным) пространством, если указано правило, по которому любым двум элементам из V ставится в соответствие третий элемент из V, называемый суммой элементов, и правило, по которому любому элементу из V и любому числу (вообще говоря, комплексному) ставится в соответствие элемент из V, называемый произведением элемента на число, и эти правила подчиняются следующим аксиомам:

• 1) / + g — g + f — коммутативный закон;
• 2) (./ + g) +hf + (g + h) — ассоциативный закон;
• 3) существует элемент 0, называемый нулей, такой, что / + 0 = 0;
• 4) для любого / существует противоположный элемент -/ такой, что / + (-/) = 0;
• 5) 1 •/ = /;
• 6) «(/ + g) = af + ag;
• 7) {a + P) f = af + Pf
• 8) (ap)f = a (Pf).

В аксиомах (5−8) 1, a, p — числа. Элементы f, g, h,…sV называются точками (или векторами).

Пример 1. Дано R' - множество вещественных чисел. Выполнение аксиом (1−8) для обычным образом определенных сложения и умножения нетрудно проверить. Таким образом, R' - это векторное пространство, точками или векторами которого служат вещественные числа. Кстати, если разместить все вещественные числа на прямой (т. е. выбрать нулевую точку, а точку р связать с числом а, если расстояние от 0 до р равно а), то и здесь векторы можно представить в виде стрелок, направленных из точки 0 в точку р.

Пример 2. Дано R"  — множество, элементом которого является любая упорядоченная совокупность из п чисел (х¹, х²,…, х") (значок над хне степень, а индекс). Число х' будем называть /-й компонентой элемента. Определим сложение элементов R" и умножение их на число покомпонентно.

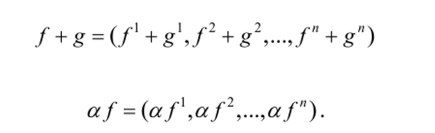
Если / = (/‘,/²,…,/") и g = (g', g²,…, g'') — элементы R" и а — число, то и.

Нулевым элементом назовем элемент (0, 0,…, 0). Аксиомы (1)—(8) снова легко проверяются, так что и множество R" является векторным пространством.

Сделаем попутно небольшое добавление к примеру 2.

Пусть Р и Q — два произвольных множества, состоящих из элементов p_i и ср соответственно. Можно образовать новое множество, элементами которого будут всевозможные упорядоченные пары (р,^,). Это новое множество называется прямым произведением множеств Р и Q и обозначается через PxQ. Пусть теперь V и W— векторные пространства. Прямое произведение V х W можно также превратить в векторное пространство, если сложение и умножение на число определить следующим образом:

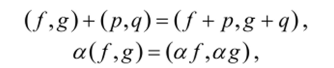
для f, p е V, g, q е W, (/, g),(p,^) eVxW и а — вещественное или комплексное число. Очевидно, пространство R" можно трактовать как прямое произведение п векторных пространств R^]

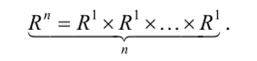
Пример 3. Пусть С — множество комплексных чисел (а + //?), где а,/3 — вещественные числа, a i — мнимая единица. Сложение и умножение на число определим следующим образом:

Нулевым назовем элемент (0 + /0). Аксиомы (1)-(8) выполняются и здесь, откуда следует, что и С также является векторным пространством.

Пример 4. Множество пхп матриц также будет векторным пространством, если сумму матриц и умножение матрицы на число определить так, как это делается в линейной алгебре, т. е. покомпонентно. Нулевым элементом этого пространства будет нулевая матрица, все элементы которой равны нулю.

Число примеров можно легко увеличить.

Если некоторое подмножество 5 векторного пространства V само образует векторное пространство, то оно называется подпространством векторного пространства V. Например, любая плоскость, проходящая через точку 0 в R³ является подпространством R так как сама является векторным пространством R². Аналогично любая прямая, походящая через точку 0, является подпространством R Кроме того, данная прямая является подпространством тех плоскостей R², в которых она лежит.

Сумма произведений ненулевых векторов на числа.

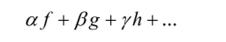
называется линейной комбинацией векторов Очевидно, если.

V — векторное пространство, то оно содержит и любую линейную комбинацию своих элементов, т. е. линейная комбинация есть вектор. Вектор, который является линейной комбинацией каких-либо других векторов, называется линейно зависимым от этих векторов. Если же он не может быть представлен в виде линейной комбинации указанного набора векторов, то он от них линейно независим. Если мы в /?' выберем какой-нибудь вектор/, не равный нулю, то все остальные векторы оказываются линейно от него зависимыми, так как могут быть записаны в виде а/, где а — число. В векторном пространстве R¹ картина другая. Выбрав ненулевой вектор /, мы не можем утверждать, что все остальные векторы будут линейно зависеть от него, поскольку векторы, линейно зависимые от f будут лежать на прямой, проходящей через точки 0 и /. Но уже двух векторов, не лежащих па одной прямой, достаточно для того, чтобы все остальные векторы линейно от них зависели. Совокупность ненулевых векторов из некоторого линейного пространства называется линейно независимой, если не существует такого ненулевого набора чисел что.

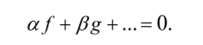
Для произвольного множества векторов максимальное число п линейно независимых векторов называется его размерностью. Так, множество точек на прямой имеет размерность один, т. е. одномерно, а множество точек на плоскости — двумерно. Если такого максимального числа не существует (число линейно независимых векторов больше любого наперед заданного числа п), то множество называется бесконечномерным, в противном случае — конечномерным.