Направленная токовая защита

Направленной называют защиту, действующую при КЗ только при определенном направлении тока КЗ или соответственно мощности КЗ, т. е. при определенном знаке тока или мощности КЗ [17, 29]. Эту защиту применяют в сетях с двухсторонним питанием, где направление тока КЗ и мощности КЗ могут иметь два противоположных направления (рис. 8.13). Направление тока КЗ и мощности КЗ зависит от места КЗ.

Рис. 8.13. Направления токов при КЗ в сетях с двухсторонним питанием

Таким образом, направление тока (мощности КЗ), проходящего по линии, характеризует, где возникло повреждение на защищаемой линии или других присоединениях, отходящих от шин данной подстанции. Это обстоятельство и используется в направленной токовой защите, которая действует только при КЗ на защищаемом участке. Простая токовая защита не может обеспечить селективность в сетях с двухсторонним питанием. Например, если КЗ произошло в точке K_t то при обычной МТЗ, когда выключатель Q2 находится ближе к месту КЗ, чем выключатель Q3, для защит А2 и АЗ должно соблюдаться условие (рис. 8.13, а)

Если же КЗ возникло в точке К₂, то ближе к месту КЗ оказывается выключатель Q3 и в этом случае должно соблюдаться условие.

Очевидно, что одновременно выполнить требования (8.18) и (8.19) невозможно и в одном из случаев защита будет действовать неселективно. Это противоречие можно устранить, если каждая из защит А2 и АЗ будет действовать только при направлении тока КЗ (мощности КЗ) от шин в линию, а при обратном направлении — блокироваться, т. е. не будет действовать. Эти направления, обозначенные стрелками на рис. 8.14, приняты за положительные. В этом случае при КЗ в точке не будет действовать защита АЗ, а при КЗ в точке К₂ не будет действовать защита А2 (рис. 8.15). Недействующие (заблокированные) при КЗ защиты и выключатели на рис. 8.15 заключены в рамки.

Рис. 8.14. Направления токов КЗ, принятые за положительные.

В этом случае можно выбирать выдержки времени защит, действующих только в одном направлении, по ступенчатому принципу с нарастанием по направлению к источнику питания (см. рис. 8.15). Для этого максимальная токовая защита дополняется органом направления мощности, в качестве которого используется реле направления мощности KW (на рисунках не показано), токовая катушка которого включена последовательно с катушкой КЛ реле тока во вторичную цепь трансформатора тока ТА соответствующей фазы. На рис. 8.13 и далее трансформаторы напряжения и тока не показаны. Катушка напряжения реле KW получает питание от трансформатора напряжения TV.

Защита приходит в действие только при одновременном срабатывании реле тока и реле направления мощности (логическая операция И). Направленная токовая защита обычно выполняется с относительной селективностью, когда время срабатывания защиты зависит от расстояния между точкой включения защиты и точкой КЗ. Первая ступень, действующая без выдержки времени, может не иметь органа направления мощности. Направления тока, при которых срабатывают реле направления мощности KW, на рис. 8.14 обозначены стрелками в направлении от шин к линии. В соответствии с указанными направлениями защиты Л1 и ЛЗ реагируют на токи, протекающие от первого источника питания, а защиты А2 и А4 — на токи от второго источника питания. Выдержки времени для защит А1, АЗ и А2, А4 выбирают по ступенчатому принципу, так же как для максимальной токовой защиты, т. е. выдержки времени для защит А1 и АЗ увеличиваются по мере приближения к первому источнику питания, а для защит А2 и А4 — по мере приближения ко второму источнику питания (рис. 8.15, в). Такой принцип определения выдержек времени направленных защит называется встречно-ступенчатым.

Таким образом, благодаря органу направления мощности все защиты разбиваются на две группы с одинаковыми положительными направлениями мощностей (А1, АЗ и А2, А4), не связанные между собой.

При КЗ в точке К_{ (рис. 8.15, а) могут прийти в действие только защиты Al, А2 и А4, для которых направление мощности совпадает с направлением стрелок, принятых за положительные направления (см. рис. 8.14), и мощности КЗ оказываются положительными. Защита АЗ блокируется реле направления мощности, так как знак мощности для этой защиты отрицательный (см. рис. 8.15, а). Защита А2 имеет меньшую выдержку времени по сравнению с защитой Л4 (рис. 8.15, г). Поэтому сработают защиты А1 и А2. На рис. 8.15, а соответствующие отключаемые защитами А1 и А2 выключатели Q1 и Q2 показаны затемненными, а заблокированная защита АЗ с соответствующим выключателем Q3 заключены в рамку.

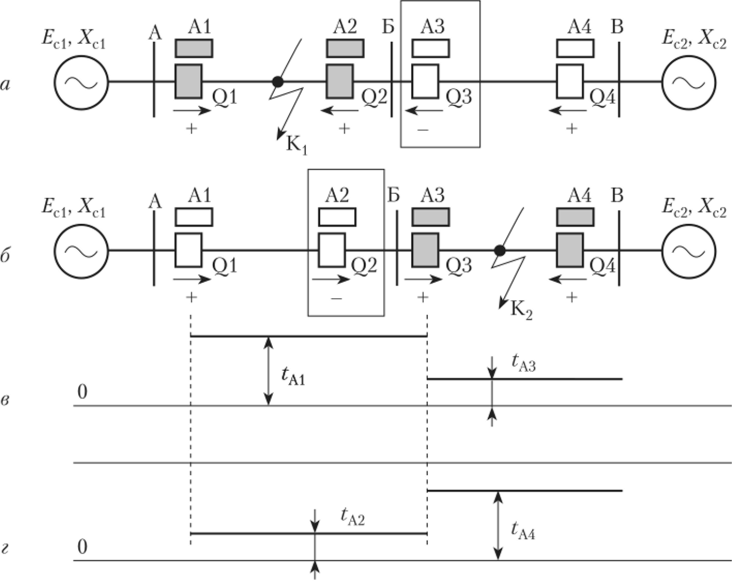
Рис. 8.15. Действие направленной токовой защиты при КЗ в точках и К_2.

При КЗ в точке К₂ (рис. 8.15, б) могут прийти в действие только защиты А1, АЗ и А4, для которых направление мощности оказывается положительным. Защита А2 блокируется реле направления мощности, так как знак мощности для этой защиты отрицательный (рис. 8.15, б). Защита АЗ имеет меньшую выдержку времени по сравнению с защитой А1. Поэтому сработают защиты АЗ и А4. Рассмотренные выше соотношения для защит А2 и АЗ при КЗ в точках K_t и К₂ поясняются с помощью векторных диаграмм на рис. 8.16, где фд-— угол сдвига фаз между синусоидами напряжения и тока короткого замыкания в месте установки защит А2 и АЗ и, соответственно, между векторами, изображающими эти синусоиды.

В качестве реле направления мощности используют индукционные или полупроводниковые реле. Принцип действия последних основан на том, что при сложении и вычитании векторов, пропорциональных напряжению и току в точке включения защиты, модули результирующих векторов получаются различными (рис. 8.17). Так, например, при положительной мощности сумма векторов получается больше, чем их разность, а при отрицательной мощности наоборот. Функциональная схема полупроводникового реле, выполненного, но указанному принципу, представлена на рис. 8.18. Схема содержит инвертор, два сумматора и компаратор К. Для увеличения чувствительности реле направления мощности вектор напряжения поворачивают на 90° или 30° в сторону отстающего тока. Схемы называются соответственно 90-градусная и 30-градусиая. В настоящее время типовой схемой является 90-градусная схема, когда в реле направления мощности токовая обмотка включается в фазу А, а обмотка напряжения включается на линейное напряжение U_BC Сигнал на выходе компаратора К (рис. 8.18) появится только в том случае, если модуль суммы векторов будет больше модуля их разности, т. е. если мощность КЗ будет положительной. В противном случае сигнал на выходе компаратора равен нулю и защита блокируется.

Рис. 8.16. Векторные диаграммы направленной защиты при КЗ в точках K_t (а) и К₂ (б).

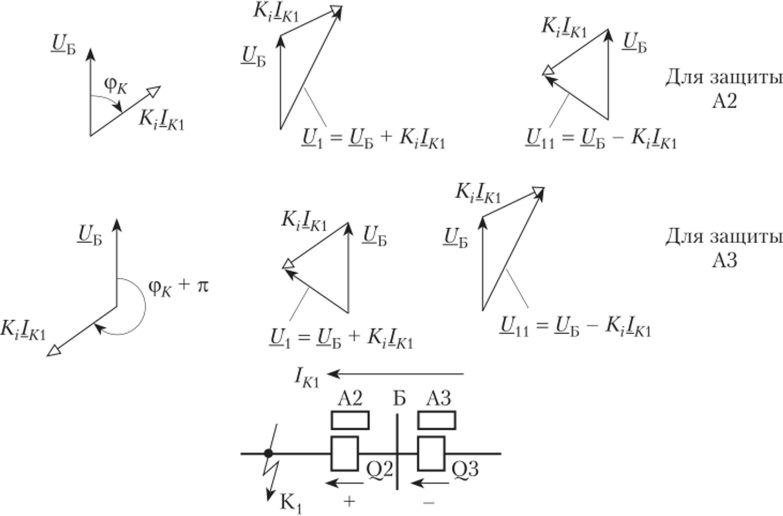
Рис. 8.17. Сложение векторов, пропорциональных напряжению и току при положительном и отрицательном направлениях мощности.

Направленная токовая защита обладает мертвой зоной, если трехфазное КЗ происходит вблизи места установки защиты, когда напряжение резко падает и реле KW не срабатывает. В сетях до 35 кВ направленная токовая защита выполняется двухфазной и является основной защитой от всех КЗ. В сетях с глухозаземленной нейтралью се используют в качестве защиты от многофазных КЗ.

Рис. 8.18. Функциональная схема полупроводникового реле направления мощности.

Рис. 8.19. Расчетная схема двух линий с двухсторонним питанием.

Рассмотрим применение интегрированного пакета Math Cad для исследования направленной токовой защиты. Расчетная схема линий АБ и БВ, защищаемых с помощью направленной защиты, приведена на рис. 8.19. Стрелками указаны направления токов, принятые за положительные. Короткие замыкания могут возникнуть на линии АБ в точке 1 (включен ключ KZ1) и на линии БВ в точке 2 (включен ключ KZ2).

Сопротивления участков первой линии обозначены Z11 и Z12, а сопротивления участков второй линии — Z21 и Z22. Сопротивления электроприемников обозначены Z1 и Z2, а сопротивления КЗ — Z1k и Z2k. ЭДС и внутренние сопротивления источников питания обозначены соответственно как Е1_У Е2 и ZG1, ZG2.

На рис. 8.20 приведены результаты решения задачи в интегрированном пакете MathCad. Точки / и 2, в которых происходит КЗ, задаются коэффициентом KZ. Если KZ = 1, замыкание происходит в точке 1 (замкнут ключ KZ1), а если KZ = 2, то в точке 2 (замкнут ключ KZ2). Сопротивления линий Z11, Z22, Z21 и Z22 задаются коэффициентами К1 и К2. Полное сопротивление первой линии обозначено ZL1, второй линии — ZL2. Сопротивление первой линии до места КЗ равно Z11 = К • ZL1. Тогда сопротивление Z12 = (1 — K1 )ZL1. Аналогично находятся сопротивления Z21 и Z22 для второй линии.

Для расчета тока КЗ для схемы, приведенной на рис. 8.19, составим девять уравнений (по числу неизвестных токов). Направления токов от шин в линию примем за положительные. Четыре уравнения составим по первому закону Кирхгофа, считая ключи KZ1 и KZ2 замкнутыми: для узла А.

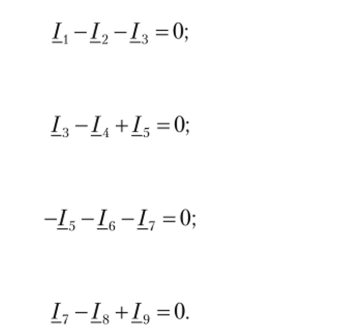
для узла 1 для узла Б для узла 2.

Оставшиеся пять уравнений составим по второму закону Кирхгофа:

На рис. 8.20 показано решение этих уравнений, записанных в матричной форме. Комплексные величины в пакете MathCad записаны без подчеркивания снизу. Решение дано для случая КЗ в точке 1 (KZ = 1). На рис. 8.20 j-4-i — мнимая единица. Искомые токи — комплексные значения и модули представлены в виде вектора (матрицы-столбца) 11. Па рис. 8.21 показаны векторные диаграммы для защит Al, А2, АЗ и А4, построенные в пакете MathCad, из которых следует, что при коротком замыкании в точке 1 (см. рис. 8.19) защита АЗ блокируется, так как направление тока и знак мощности для этой защиты отрицательные.

На рис. 8.22 показаны векторные диаграммы защит А1 и АЗ в виде суммы и разности векторов напряжения и тока. Коэффициент пропорциональности тока взят равным пяти. Из рис. 8.22 следует, что для защиты А1 сумма векторов больше их разности и защита А1 срабатывает, а для защиты АЗ сумма векторов меньше их разности. Для защиты А1 мощность положительная, а для защиты АЗ — отрицательная, и защита АЗ блокируется. Сложение и вычитание векторов для определения знака мощности показано на рис. 8.22. Этот алгоритм определения знака мощности реализуется схемой, приведенной на рис. 8.18.

Рис. 8.20. Исследование направленной токовой защиты в интегрированном пакете MathCad.

На рис. 8.23 показан алгоритм срабатывания защит Al, А2, АЗ и А4. Для описания функций защит использована функция с условием if. Срабатывание защиты обозначено цифрой 1, а несрабатывание — цифрой 0. Как следует из рис. 8.23, при КЗ в точке 1 блокируется защита АЗ, а из двух защит А2 и А4 срабатывает защита с меньшей выдержкой времени, т. е. защита А2. Окончательный результат — сработают защиты А1 и А2. Аналогично производится расчет для КЗ в точке 2.

Таким образом, наличие органа направления мощности позволяет при выборе значений токов срабатывания учитывать только те режимы, при которых мощность направлена от шин в линию. При этом чувствительность токовых отсечек повышается.

Рис. 8.21. Векторные диаграммы для направленных защит Al, А2, АЗ и А4.

Рис. 8.22. Сложение и вычитание векторов напряжения и тока для защит А1 и АЗ.

Рис. 8.23. Алгоритм срабатывания направленных защит Al, А2, АЗ и А4.