Переводы, функторы и естественные преобразования

Так же как в логике существуют переводы между логическими исчислениями, в категорной логике существуют соответствующие переводы между дедуктивными системами. Что касается логики, то здесь понятие перевода между исчислениями можно сформулировать следующим образом.

Пусть Т и Т₂— исчисления, сформулированные, соответственно, в языках L и L₂ с соответствующими логиками. Пусть <�р — рекурсивная функция, сопоставляющая формуле языка L формулу языка L₂. Функцию будем называть переводом исчисления Т в Ть если и только если выполняется условие АеТ |=> ср (Л)еТ₂. Если выполняется дополнительное условие <�р(Л)еТ₂ |=> АеТ, то рекурсивную функцию ср будем называть погружающей операцией Т в Т₂. Исчисление Т погружаемо в исчисление Т₂, если и только если существует рекурсивная функция, погружающая Т в Т₂. [Смирнов 2002, с. 120].

В случае дедуктивных систем нам уже недостаточно говорить только лишь о функции, переводящей формулы одной системы в формулы другой — нам требуется еще говорить о переводе кодов, т .е. еще об одной функции, сопоставляющей друг другу различные виды доказательств. Определим морфизм графов М из графа G в граф Н как пару функций, записывая эту пару как М, сопоставляющих каждому объекту А из G объект МЛ из Н, а каждой стрелке /? Ah В из G стрелку M (f): M (A)h М (В) из Н.

Обозначим для удобства дальнейшего изложения дедуктивную систему как тройку (D, !,<�•), где D будет представлять собой граф, 1 есть тождество в D, а⁰ есть композиция в D. Тождество и композиция в различных дедуктивных системах всегда будем обозначать одними и теми же символами 1 и °, предполагая, что из контекста ясно, какой дедуктивной системе они принадлежат.

Функтор F из дедуктивной системы (0,1,°) в дедуктивную систему (Е, 1,°) будет представлять собой морфизм графов из D в Е, такой, что следующие тождества справедливы для Е:

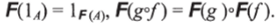
Все же главный интерес будут представлять как раз не переводы из одной дедуктивной системы в другую, а переводы дедуктивных категорий, поскольку именно в дедуктивных категориях мы имеем дело с точно описанной структурой на доказательствах, обусловленной наличием тождеств между стрелками. Роль переводов между дедуктивными категориями также выполняют функторы, которые определяются совершенно аналогично функторам между дедуктивными системами:

Функтор F из дедуктивной категории С в дедуктивную категорию D представляет собой функцию, сопоставляющую каждому объекту А категории С объект F (A) категории D, а каждой стрелке/• АВ категории С стрелку F (f): F (A)h F (B), такую, что.

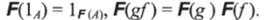
В будущем нам понадобится следующее определение:

Определение. Если А и В являются объектами дедуктивной категории С, то обозначим как Аггс (А, В) класс всех стрелок (доказательств) Ah В в С. Если окажется, что Аггс (А, В) есть множество для любых объектов А и В, то про дедуктивную категорию С говорят, что она является локально малой категорией.

Будем опускать нижний индекс в выражениях типа Аггс{АД), если из контекста ясно, о какой категории идет речь. Полезность введения этого понятия видна из следующего определения:

Определение. Будем говорить, что А является инициальным объектом категории С, если Аггс (А, В) содержит не более чем один элемент. Дуально, будем говорить, что В является терминальным объектом категории С, если Аггс (А, В) содержит не более чем один элемент.

Следует учесть, что функторы могут обладать еще одной особенностью, связанной с. ориентацией стрелок: нетрудно предвидеть случай, когда функтор заменяет все стрелки на противоположно направленные. В этом случае мы будем говорить, что функтор ковариантен, если он не меняет направление стрелок в результирующей категории, и что функтор контравариантен, если он меняет направление стрелок на противоположное.

В современной логике часто рассматривают не одну, а несколько логических систем, анализируя их и сравнивая между собой. И в этом случае речь неминуемо заходит и о сравнении переводов из одной системы в другую и их свойствах, тем более, что, как правило, между системами существует не один-единственный перевод, а несколько. Чтобы сделать подобный разговор точным и учесть это обстоятельство, вводится понятие «естественного преобразования» между функторами.

Пусть F и G будут функторами из С в D. Естественное преобразование из F в G есть семейство р стрелок р^: F (А) — G (А) категории D, свое для каждого объекта А категории С, такое, что для каждой стрелки f: АВ категории С верно следующее тождество:

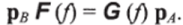
В подобных тождествах нижний индекс обычно опускается и может быть восстановлен по контексту. Стрелки р_А, принадлежащие семейству р, называются компонентами естественного преобразования .

Альтернативное определение естественного преобразования выглядит следующим образом:

Естественное преобразование из F в G есть семейство операций Р^в_А, по одной для каждого объекта А категории С, применение которых к стрелке g: G (А) — D категории D порождает стрелку P^G_A (g): F (А)ЬD, такую, что выполняются следующие тождества:

Каждое естественное преобразование в этом новом смысле при использовании определения.

(i)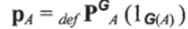

порождает естественное преобразование р в старом смысле, когда каждое естественное преобразование р в старом смысле при использовании определения.

(ii)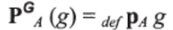

порождает естественное преобразование Р в новом смысле. Более того, если мы будем исходить из P^G и получим р с помощью определения (i), а затем определим Р⁶ по определению (ii), мы опять вернемся к исходному P^G. Сходным образом, если мы будем исходить из р и получим P^G с помощью (ii), а затем определим р по (i), мы опять вернемся к исходному р. Для этого следует проверить, что для исходного P^G тождество (ii) имеет место при замене р^ в правой части согласно (i), а затем, что для исходного р тождество (i) выполняется в случае, если мы заменяем Р°_А в правой части согласно (ii). Отсюда оба понятия естественного преобразования будут иметь тот же самый объем. В этом случае говорится, что два понятия естественного преобразования экстенсионально эквивалентны относительно определений (i) и (ii).

Еще одной экстенсионально эквивалентной альтернативой является определение естественного преобразования как семейства операций P^F_Ay которые, будучи применены к стрелке g: DF (А) категории D, порождают стрелку Р^F_A(g):D-G (A) категории D, такую, что выполняются следующие тождества:

G (/) Р^F(h) = P^f(F (f)h), P^F(h)g = P^F(hg).

Если G является одно-однозначной функцией на объектах, то можно заменить семейство операций Р°^ на единственную операцию, а если F точно так же является одно-однозначной функцией на объектах, то можно сделать то же самое и для P^F.