Построение двойственной задачи

Двойственная обратная задача — задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой, задачи. В литературе по линейному программированию в большинстве случаев рассматриваются формулировки двойственной задачи, соответствующие различным формам записи прямой задачи, которые, в свою очередь, определяются типом ограничений, знаками переменных и направлением оптимизации (максимизация или минимизация).

Рассмотрим обобщенную формулировку двойственной задачи линейного программирования, которая применима к любой форме представления прямой задачи. В основу такой формулировки положен тот факт, что использование симплекс-метода требует приведения любой задачи линейного программирования к стандартной форме. Так как все методы вычислений, основанные на соотношениях двойственности, предполагают непосредственное использование симплекс-таблиц, формулировка двойственной задачи в соответствии со стандартной формой прямой задачи представляется достаточно логичной. Следует, однако, помнить, что приводимая ниже формулировка двойственной задачи является обобщенной в том смысле, что она применима ко всем формам прямой задачи.

Прямая задача линейного программирования в стандартной форме записывается следующим образом:

при ограничениях.

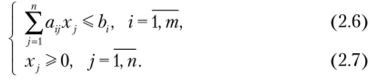
Чтобы сформулировать условия двойственной задачи, проведем симметричное структурное преобразование условий прямой задачи в соответствии со следующими правилами:

• 1) каждому ограничению прямой задачи соответствует переменная двойственной задачи;
• 2) каждой переменной прямой задачи соответствует ограничение двойственной задачи;
• 3) коэффициенты при некоторой переменной, фигурирующие в ограничениях прямой задачи, становятся коэффициентами левой части соответствующего ограничения двойственной задачи, а коэффициент, фигурирующий при той же переменной в выражении для целевой функции прямой задачи, становится постоянной правой части этого же ограничения двойственной задачи.

Па примере задачи планирования товарооборота двойственная задача формулируется следующим образом: определить оценку (неявную стоимость) единицы каждого вида ресурсов yj (i = 1, т), чтобы при заданных объемах ресурсов b_jt прибыли Cj, нормах расхода ресурсов минимизировать оценку всех ресурсов торгового предприятия, затраченных на организацию торгового процесса.

Запишем математическую модель двойственной задачи.

Определить вектор У = г/₂,…, у_т), который удовлетворяет ограничениям.

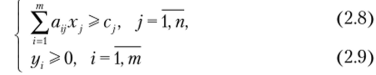
и обеспечивает минимальное значение целевой функции.

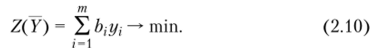
Ограничения (2.8) показывают, что стоимость всех ресурсов, затраченных на продажу единицы j-й группы товаров, должна быть не меньше дохода, получаемого при реализации единицы j-й группы товаров, а общая стоимость всех ресурсов должна быть минимизирована.

В целом двойственная задача по отношению к исходной составляется согласно следующим правилам.

• 1. Число переменных в двойственной задаче равно числу ограничений в прямой задаче.
• 2. Матрица коэффициентов системы ограничений двойственной задачи получается из матрицы коэффициентов системы ограничений прямой задачи путем транспонирования.
• 3. Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи.
• 4. Свободными членами системы ограничений двойственной задачи являются коэффициенты функции цели прямой задачи.
• 5. Двойственная задача решается на минимум, если целевая функция прямой задачи задается на максимум, и наоборот.
• 6. Коэффициентами функции цели двойственной задачи служат свободные члены системы ограничений прямой задачи.
• 7. Если переменная прямой задачи х_} > 0, то j-e условие системы ограничений двойственной задачи является неравенством, если Xj — любое число, тоу-е условие двойственной задачи представляет собой уравнение.
• 8. Если i-e соотношение прямой задачи является неравенством, то соответствующая оценка i-го ресурса — переменная г/, > 0, если i-e соотношение представляет собой уравнение, то переменная двойственной задачи у,• — любое число.

Решение прямой задачи дает оптимальные объемы в структуре товарооборота торгового предприятия, а решение двойственной — оптимальную систему оценок ресурсов, используемых для реализации товаров.