Решение игр в чистых стратегиях

Чистая стратегия — детерминированный (исключающий случайности) план действий. В предыдущей главе мы рассматривали только чистые стратегии. Смешанные стратегии будут обсуждаться в параграфе 2.2, а пока, если не оговорено иного, под стратегией мы всегда имеем в виду чистую стратегию.

Очень часто в процессе изложения мы будем иллюстрировать концепции решения примерами биматричных игр, поэтому дадим соответствующие определения.

Определение 2.1. Конечной игрой называется игра, в которой множество игроков и множества стратегий каждого игрока содержат конечное число элементов. Конечная игра двух лиц называется биматричной игрой.

Последнее наименование происходит от удобной формы записи выигрышей в такой игре — с помощью двойной матрицы.

Для последующего анализа удобно разделить стратегии в произвольном профиле стратегий s на стратегию некоторого /-го игрока s, и стратегии всех остальных игроков s_₍. Формально s = (.у, s ,). Здесь не подразумевается, что мы меняем местами координаты профиля стратегий, мы лишь вводим другой способ его обозначения.

Первой концепцией решения игры, которую мы рассмотрим, будет равновесие в доминирующих стратегиях.

Определение 2.2. Стратегия /-го игрока у строго доминирует его стратегию s', если Uj (s_jt s ,) > h,(s', s ,) для любого набора s, стратегий остальных игроков. При этом стратегия s' называется строго доминируемой.

Содержательно это означает, что при любом фиксированном наборе стратегий остальных игроков /-Й игрок, выбирая стратегию s, получает строго больший выигрыш, чем при выборе стратегии s'. Логично предположить, что рациональный игрок не должен выбирать строго доминируемые стратегии. Такое предположение в простейших играх может оказаться достаточным для нахождения решения игры.

Определение 2.3. Профиль стратегий s* = (s*, s^,…, s*) называется равновесием в (строго) доминирующих стратегиях, если для любого /-го игрока стратегия s' строго доминирует любую другую его стратегию.

Может показаться, что данная концепция решения может привести лишь к тривиальным выводам. Каждый игрок имеет среди своих стратегий такую, которая даст ему выигрыш больше, чем любая другая, как бы ни действовали оппоненты. Тогда он будет применять именно эту стратегию в равновесии. Все довольно очевидно. Но именно такая ситуация характерна для, пожалуй, самой известной и весьма важной для анализа ряда практических ситуаций игры «дилемма заключенных».

Пример 2.1 (дилемма заключенных). Два преступника находятся под стражей в разных камерах и не могут переговариваться. Следствие располагает достаточной доказательной базой, чтобы осудить каждого из них за незначительное преступление на один год. Но по крупному преступлению, за которое преступникам грозит уже десять лет заключения, улик у следствия недостаточно. Представители следствия предлагают каждому из преступников сделку: преступник получит срок на один год меньше, если он даст свидетельство против своего напарника, которого будет достаточно для обвинения последнего, но крупному преступлению. Предположим, что преступников беспокоит только число лет, которое они проведут в тюрьме, каждый дополнительный год дает минус единицу полезности. Тогда выигрыши преступников могут быть представлены следующей двойной матрицей:

В случае, когда участники игры не названы по именам, мы будем считать, что разным стратегиям первого участника соответствуют строки двойной матрицы, а стратегиям второго участника — столбцы. Если в нашем примере первый заключенный даст показания, а второй не будет их давать, то первый будет отпущен на свободу, а второй получит десять лет тюрьмы.

Легко заметить, что, как бы ни действовал другой заключенный, выигрыш больше (срок заключения меньше), если давать показания (для первого игрока первые координаты в первой строке двойной матрицы строго больше, чем во второй строке, для второго игрока вторые координаты в первом столбце двойной матрицы строго больше, чем во втором столбце). Тогда равновесием в доминирующих стратегиях будет профиль стратегий (дать показания, дать показания).

Интересно в данном примере то, что игроки, выбирая поведение, которое увеличивает их выигрыш, приходят к ситуации, где их выигрыши низки по сравнению с противоположной ситуацией — когда оба выбирают молчать. Объяснение кроется в наличии сильного внешнего эффекта, т. е. сильного влияния действий одного игрока на выигрыши другого игрока. В результате равновесный профиль стратегий оказывается единственным неэффективным по Парето в данной игре. Отметим, что эффективность по Парето, желательная с точки зрения участников игры, может быть отнюдь не желательной с общественной точки зрения, как в данном случае.

Ситуации, подобные дилемме заключенных, часто встречаются при анализе экономических ситуаций. Рассмотрим, например, конкуренцию между двумя магазинами, торгующими близким набором продуктов. Для простоты предположим, что магазины могут назначать только два уровня цен — высокий или низкий. Потребители, естественно, предпочитают покупать в магазине с более низкими ценами. Тогда выигрыши магазинов, характеризующиеся их прибылью, могут выглядеть, например, следующим образом:

С точки зрения равновесия ситуация здесь аналогична дилемме заключенных — равновесие в доминирующих стратегиях (низкие цены, низкие цены) является единственным неэффективным по Парето профилем (и тоже желательным с общественной точки зрения).

Уже упомянутая широкая известность дилеммы заключенных стала причиной того, что на ее примере экспериментально пытались проверить корректность предсказаний теории игр. Проверка состояла в том, что двум незнакомым людям предлагалось сыграть в игру на деньги с призами (например, в долларах), близкими к тем, что указаны для игры двух магазинов. Каждый из участников принимал решение отдельно (часто — анонимно) и не знал до получения выигрыша решения другого игрока. Выяснилось, что в таких условиях во многих разыгрываниях игры игроки приходили не к равновесному результату, если предположить, что денежные призы корректно оценивают их выигрыши. Конечно, из результатов этих экспериментов не следует, что предсказания теории игр некорректны, а следует лишь то, что, оценивая свой выигрыш, игроки принимали во внимание неденежные факторы — соображения альтруизма, справедливости и т. п. Если выигрыши игроков оценены корректно, то игроки должны предпочитать доминирующую стратегию, а значит, и выбирать ее (в духе выявленных предпочтений в микроэкономике). Поэтому ценность экспериментов такого рода — не в проверке теоретико-игровых предсказаний, а в оценке роли нематериальной мотивации в действиях индивидов.

Значительно меньше, чем концепция строго доминирования, в теории игр используется концепция слабого доминирования.

Определение 2.4. Стратегия /-го игрока s, слабо доминирует его стратегию s', если m,(s, s ,) > m_;(sJ, s ,) для любого набора стратегий остальных игроков s_j, причем хотя бы для одного набора стратегий других игроков неравенство выполняется строго. Тогда стратегия s' называется слабо доминируемой.

В случае нестрогих неравенств уже нет возможности утверждать, что рациональный игрок не выберет слабо доминируемую стратегию, хотя такое поведение и представляется довольно логичным. Существует, хотя и редко применяется, аналогичное случаю строго доминирования определение равновесия в слабо доминирующих стратегиях.

Определение 2.5. Профиль стратегий s* = (s*, Sj,…, s*) называется равновесием в слабо доминирующих стратегиях, если для любого /-го игрока стратегия s' слабо доминирует любую другую его стратегию.

Пример 2.2 (закрытый аукцион второй цены). Среди двух лиц проводится закрытый аукцион второй цены. Аукцион устроен следующим образом. Каждый из участников указывает неотрицательную ставку, не зная ставок других участников (в конверте). Участник, сделавший наибольшую ставку, выплачивает максимальную сумму среди ставок других участников (т.е. сумму второй, но величине ставки) и получает некоторый предмет. Если, например, ставки игроков составили 100 и 90, то побеждает в аукционе участник, сделавший ставку 100, он приобретает предмет за 90 — размер второй ставки. Пусть каждый участник имеет оценку предмета, выраженную в денежных единицах, v₂ > 0. Эти оценки известны всем участникам. Пусть при этом для простоты описания игры если оба участника указывают одинаковую ставку, то предмет достается первому участнику.

В данной игре стратегией первого игрока s, будет размер его ставки. Так как ставка неотрицательна, множество всех его возможных стратегий.

5, = [0; °о). Аналогично стратегией второго игрока s₂ будет размер его ставки, и 5₂ = 10; °о). В отличие от предыдущих примеров набор стратегий в данном случае является непрерывным, а не дискретным. Поэтому представить функцию выигрыша таблично в данном случае не получится. Выигрыш первого игрока определяется следующим образом:

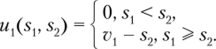
Выигрыш второго игрока определяется аналогично:

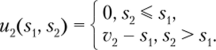
Можно проверить, что в данной игре профиль стратегий, когда каждый игрок называет в качестве ставки свою оценку s* = (у, v₂), является равновесием в слабо доминирующих стратегиях. Покажем, что стратегия первого игрока — называть свою оценку — слабо доминирует любую другую его стратегию. Для этого нам нужно перебрать все остальные стратегии первого игрока. Рассмотрим два возможных случая.

• 1. Пусть первый игрок делает ставку s', ниже своей оценки. Тогда если второй игрок делает ставку не выше s', то первый игрок в любом случае выигрывает аукцион, и обе стратегии — называть свою оценку или ниже своей оценки — приносят одинаковый выигрыш, равный «, — s₂. Если второй игрок делает ставку выше оценки первого игрока, то первый игрок в любом случае проигрывает аукцион и получает ноль. Если же второй игрок делает ставку в интервале (s', о,), то стратегия s', приносит выигрыш ноль, так как тогда первый игрок проигрывает аукцион, в то время как сделав ставку, равную своей оценке, первый игрок выиграет аукцион и получит выигрыш
• — s₂ > 0. Таким образом, при условиях s₂ < s' и s₂ > и, выполняется равенство u_t(v, s₂) = и, (s', s₂), а при условии s₂ e (s', v_t) выполняется неравенство и,(г>, s₂) > w,(s', s₂). Следовательно, по определению, стратегия v_{ слабо доминирует стратегию s',.
• 2. Пусть первый игрок делает ставку s, выше своей оценки. Тогда при s₂ < v_t выполняется «,(?;, s₂) = m,(s, s₂) = г>, — s₂, при s₂ > s, выполняется «,(», s₂) = w,(s, s₂) = 0, a npns₂ e (a, s,] выполняется 0 = и,(о, s₂) > w,(s, s₂) = = ц, — s₂ < 0. Следовательно, по определению, стратегия v_x слабо доминирует стратегию s,.

Мы показали, что для первого игрока стратегия назвать свою оценку в качестве ставки слабо доминирует любую другую стратегию. Легко проверить, что аналогичное утверждение верно и для второго игрока. Отметим, что в нашем рассуждении мы нигде не использовали тот факт, что игрок знает оценку другого игрока, а значит, и в случае игры с неполной информацией в закрытом аукционе второй цены называть свою оценку будет не менее выгодно, чем делать любую другую ставку.

Может показаться, что для продавца невыгодно устраивать аукцион второй цены, когда он может устроить аукцион первой цены и получать величину не второй, а первой ставки. Однако и величина ставок в случае аукциона первой цены в равновесии будет ниже. Подробнее о доходности аукционов мы поговорим в гл. 5. Пока же отметим, что аукцион второй цены очень поиулярен и широко используется, например, компаниями Google и «Яндекс» при продаже контекстной рекламы в Интернете^[1].

Равновесие в доминирующих стратегиях существует лишь в небольшом классе игр. Обычно у игроков нет единственной стратегии, которая доминирует все прочие. Но концепция доминирования позволяет находить решения в более широком классе игр. Для этого нужно вести последовательные рассуждения о действиях игроков. Мы уже отмечали, что рациональный игрок не будет выбирать строго доминируемую стратегию. Но это означает, что другой игрок может вести анализ игры, игнорируя возможность выбора оппонентом такой стратегии. Возможно, при гаком анализе выяснится, что у другого игрока есть доминируемая стратегия, которая не была доминируемой в исходной игре. И так далее. Дадим формальное определение.

Процесс последовательного исключения строго доминируемых стратегий задается следующим образом. Исключим все строго доминируемые стратегии игроков из рассмотрения, т. е. рассмотрим новую игру, в которой из множества возможных стратегий игроков исключены все доминируемые стратегии. Затем в этой новой игре исключим все строго доминируемые стратегии и т. д.

Возможно, такой процесс завершится, когда у игроков останется по нескольку стратегий, но возможно, что каждый игрок будет иметь лишь одну неисключенную стратегию, тогда логично считать набор из этих стратегий решением игры.

Определение 2.6. Если в результате последовательного исключения строго доминируемых стратегий у каждого игрока остается единственная стратегия, то профиль этих стратегий называется равновесием по доминированию.

В примере 1.1 мы получили именно такое равновесие. Рассмотрим еще один пример.

Пример 2.3 (выборы)^[2]. Население страны (всего 90 млн избирателей) но своей идеологии делится на 5 групп в следующем соотношении: крайне левые — 10 млн, левые — 40 млн, центристы — 10 млн, правые — 10 млн, крайне правые — 20 млн. Два кандидата в президенты независимо друг от друга выбирают свою идеологическую платформу — одну из перечисленных пяти позиций. Каждый избиратель голосует за того кандидата, который ближе к его идеологии. Равноудаленные избиратели равновероятно выбирают одного из кандидатов. Например, если первый кандидат выбирает центристскую позицию, а второй — крайне правую, то крайне левые, левые, центристы и половина правых голосуют за первого кандидата, остальные — за второго, и кандидаты получают соответственно 65 млн и 25 млн голосов. Пусть кандидаты заботятся только о том, чтобы набрать по возможности большее число голосов (идеология их совершенно не интересует).

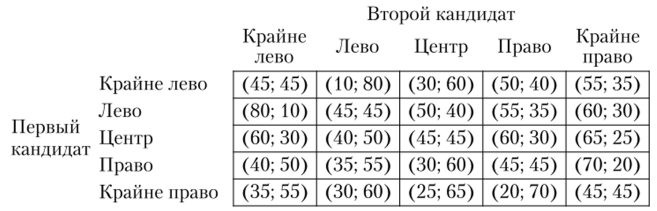
Можно заметить, что для каждого кандидата стратегия «Лево» строго доминирует стратегию «Крайне лево» и стратегия «Право» строго доминирует стратегию «Крайне право». Тогда, исключая стратегии «Крайне лево» и «Крайне право», получаем следующую игру.

В получившейся новой игре у каждого игрока снова имеются строго доминируемые стратегии. Стратегия «Центр» строго доминирует стратегию «Право». Отметим, что в первоначальной игре стратегия «Право» не была доминируемой. Исключая стратегию «Право», получаем двойную матрицу:

А теперь в получившейся игре для каждого игрока стратегия «Лево» строго доминирует стратегию «Центр». Исключая стратегию «Центр», получаем равновесие по доминированию s* = (Лево, Лево).

Данный пример иллюстрирует утверждение, получившее название «теорема о медианном избирателе». Если политики заинтересованы только в получении максимального числа голосов и могут выбирать свою позицию произвольно, кандидатов только двое, а предпочтения избирателей (которые голосуют за ближайшего к их позиции кандидата) можно упорядочить на отрезке, то в равновесии оба политика выберут позицию медианного избирателя. Конечно, в реальной политической жизни вряд ли можно встретить ситуацию, когда кандидаты выбирают позицию произвольно.

Еще одна ситуация, в которой медианное положение оказывается равновесным, связана с моделью Хотеллинга линейного города с выбором продавцами местоположения при фиксированных ценах. Заменим в примере 2.3 кандидатов в президенты на магазины, политический спектр — на главную улицу небольшого города, а избирателей — на покупателей, приобретающих ровно одну единицу продукции в ближайшем магазине. В этом случае мы получим указанную модель Хотеллинга. Важно, что при этом магазины не могут варьировать цену на продукцию, тем самым привлекая более далеко расположенных потребителей. В противном случае решение модели Хотеллинга может быть иным.

Равновесие в доминирующих стратегиях является частным случаем равновесия по доминированию, когда единственный профиль стратегий остается уже после первого шага последовательного исключения строго доминируемых стратегий. Отметим, что для слабого доминирования процесс последовательного исключения доминируемых стратегий не применяется. Причины мы обсудим чуть позже. А сейчас введем основополагающее для всей теории бескоалиционных игр определение.

Определение 2.7. Профиль стратегий s* = (s*, sj,…" s*) называется равновесием по Нэшу^[3] {равновесием Нэша), если для любого /-го игрока и любой его стратегии s, е S_i выполняется неравенство.

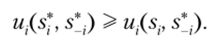
О чем содержательно говорит данное определение? Зафиксируем равновесные стратегии всех игроков, кроме одного. Тогда этому последнему игроку равновесная стратегия приносит выигрыш не меньший, чем любая другая. Иначе говоря, если все остальные игроки применяют свои равновесные стратегии, то ни у одного из игроков нет возможности с выгодой отклониться от равновесной стратегии в одиночку. Ключевой момент здесь заключается в том, что мы рассматриваем только возможности отклониться в одиночку, а не совместно.

Очевидно, данное определение можно представить в альтернативной эквивалентной форме.

Определение 2.7'. Профиль стратегий s* = (s*, s*₂,…, s*) называется равновесием по Нэшу, если для любого i-го игрока выполняется условие.

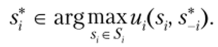
В определении говорится, что при равновесных стратегиях других игроков равновесная стратегия данного игрока максимизирует его полезность, т. е. является элементом множества стратегий, которые максимизируют его функцию полезности. Это множество может, естественно, состоять не из единственного элемента. Последний вариант определения наводит на идею поиска равновесий по Нэшу, связанную с понятием наилучшего ответа.

Определение 2.8. Стратегия /-го игрока s' называется наилучшим ответом на набор стратегий остальных игроков s ., если.

Отображение наилучшего ответа 3, ставит в соответствие любому набору стратегий остальных игроков s__{ множество всех наилучших ответов /-го игрока на данный набор стратегий, т. е.

В равновесии, но Нэшу, но определению каждый игрок выбирает наилучший ответ на равновесные стратегии оппонентов. Тогда метод поиска равновесий, но Нэшу будет заключаться в следующем — найдем отображения наилучшего ответа для каждого игрока, а затем найдем пересечения этих отображений в пространстве профилей стратегий, т. е. такие профили s* = = (.s'*, Лр …, s*)_} в которых для любого игрока i е I s* е у (лТ). Проиллюстрируем указанный метод на примере.

Пример 2.4 (семейный спор). Семейная пара решает, как провести вечер. Имеются два варианта — пойти на балет или на футбол. Он и она принимают решение о том, куда пойти, независимо друг от друга (что, вероятно, не слишком логично, но таковы условия нашей игры). Идти куда-то в одиночку никому не хотелось бы, но любимое времяпровождение у участников различается. Двойная матрица выигрышей имеет следующий вид:

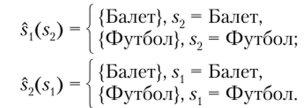
В данной игре ни у одного из игроков нет строго доминируемых стратегий, поэтому нет равновесия по доминированию. Наилучшим ответом на стратегию оппонента «Балет» является стратегия «Балет», а наилучшим ответом на стратегию «Футбол» — стратегия «Футбол». Тогда отображения наилучшего ответа можно записать следующим образом:

В биматричной игре нагляднее помечать наилучшие ответы непосредственно в двойной матрице выигрышей. Сравнив первые координаты в каждом столбце двойной матрицы и вторые координаты в каждой строке (при фиксированной стратегии оппонента), пометим наибольшие из них, что будет соответствовать наилучшему ответу. Получим:

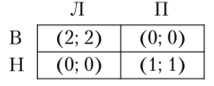
Пересечением наилучших ответов являются элементы двойной матрицы, в которых обе координаты помечены. Таким образом, игра имеет два равновесия по Нэшу (в чистых стратегиях): s* = (Балет, Балет) и s* = (Футбол, Футбол).

Отметим, что в отличие от равновесия по доминированию концепция равновесия по Нэшу не гарантирует единственности полученного предсказания разыгрывания игры, как очевидно и из примера 2.4. С одной стороны, это огорчает, но с другой — в реальности мы наблюдаем различия в поведении людей в аналогичных ситуациях. Например, в некоторых странах существует левостороннее движение транспорта, а в некоторых — правостороннее. В нашем примере выбор равновесия может зависеть, например, от того, кто более склонен пойти на уступки — он или она, или от того, куда принято ходить в этот день недели. Когда потери от отсутствия координации велики, как в случае с дорожным движением, общество обычно вырабатывает традиции или законы, которые регулируют выбор равновесия.

В примере 2.4 оба равновесия были эффективными, но Парето. Но что если одно из равновесий является Парето-улучшенисм по сравнению с другим? Можем ли мы утверждать, что в этом случае будет выбрано более эффективное равновесие? Рассмотрим, например, такую двойную матрицу выигрышей:

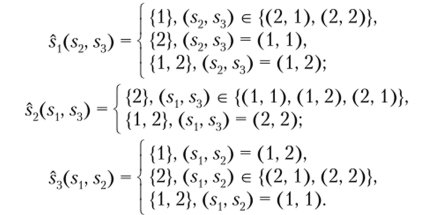
В этой игре снова два равновесия (В, Л) и (Н, П), но теперь равновесие (В, Л) Парето-доминирует равновесие (Н, П). Можно ожидать, что в такой игре игроки будут выбирать стратегии в соответствии с равновесием (В, Л), но когда игроков становится больше, переход к эффективному равновесию может быть затруднен из-за необходимости совместно изменить свои действия.

Пример 2.5 (выбор времени посева)^[4]. Паланпур является бедной деревней даже по стандартам Индии. Боулз рассказывает о встрече с местным крестьянином, возделывающим свой участок поля. Речь зашла о том, что жители Паланпура засевают поле на несколько недель позже срока, который обеспечил бы максимум урожая. Крестьяне знают, что, засеяв поле раньше, они получат больший урожай, но ни один из них не хочет засевать свой участок первым, потому что тогда семена склюют птицы. Если бы удалось совместно изменить срок посева, то урожаи бы возросли, но крестьяне не знают, как это сделать.

Следующий пример не связан ни с какой реальной ситуацией и носит чисто технический характер. Обычно увеличение числа игроков вызывает у студентов, изучающих теорию игр, некоторые сложности. Рекомендуем читателю внимательно изучить данный пример.

Пример 2.6 (игра трех игроков). Пусть в игру играют три игрока. Их выигрыши представлены в следующих двух таблицах:

Здесь двум стратегиям первого игрока (1 и 2) соответствуют строки таблиц, двум стратегиям второго игрока (1 и 2) соответствуют столбцы таблиц, а двум стратегиям третьего игрока (1 и 2) — разные таблицы. Номер координаты в векторе выигрышей соответствует номеру игрока. Например, м₂(2, 2, 1) = 9.

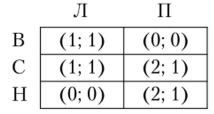
Отметим наилучшие ответы непосредственно в таблицах:

В игре два равновесия по Нэшу (в чистых стратегиях): s* = (1, 2, 1) и s* = = (2, 1, 2). Отметим также, что у второго игрока вторая стратегия слабо доминирует первую стратегию, что не противоречит наличию равновесия, в котором второй игрок играет свою первую стратегию. Эффективными, но Парето профилями стратегий в данной игре являются (1,2, 1), (2, 2, 1), (1,2, 2) и (2, 2,2).

Исключение слабо доминируемых стратегий не используется для решения игр отчасти из-за того, что при таком исключении могут быть исключены некоторые равновесия по Нэшу, как в примере 2.6. Другая проблема, возникающая при исключении слабо доминируемых стратегий, состоит в том, что набор оставшихся стратегий может зависеть от порядка исключения. В качестве примера можно рассмотреть игру со следующей двойной матрицей выигрышей:

Если в данной игре сначала исключить стратегию В первого игрока, поскольку она слабо доминируема стратегией С, а затем исключить стратегию Л второго игрока, поскольку она в получившейся игре слабо доминируема стратегией II, то в игре останутся профили (С, II) и (Н, II). Если же сначала исключить стратегию Н первого игрока, поскольку она слабо доминируема стратегией С, а затем исключить стратегию П второго игрока, поскольку она в получившейся игре слабо доминируема стратегией Л, то в игре останутся профили (В, Л) и (В, С). Можно избежать такой ситуации, например, введя правило сначала найти все слабо доминируемые стратегии, которые существуют в текущей игре, а лишь потом одновременно исключить их. Но как обосновать применение именно такого правила? Для строгого доминирования порядок исключения стратегий значения не имеет.

Связь между концепциями равновесия по доминированию и равновесия по Нэшу раскрывают следующие два утверждения, которые мы приведем с доказательством.

Утверждение 2.1. Если в игре профиль чистых стратегий s* = (s', Sj,…, s') является равновесием по Нэшу (в чистых стратегиях), то составляющие его стратегии не могут быть исключены при последовательном исключении строго доминируемых стратегий.

Доказательство. Будем вести доказательство от противного.

Предположим, что профиль s* = (s', s%,…, s') образует равновесие по Нэшу, и в некоторый момент одна из стратегий s* этого профиля исключается как строго доминируемая. Мы будем рассматривать первую из таких стратегий, которая была исключена. Отмстим, что в этот момент еще ни одна стратегия из набора s*_i не была исключена.

Если профиль s* = (s', s*₂,…, s') является равновесием по Нэшу, то по определению для любого i е I и для любой стратегии s, е 5, выполняется неравенство.

Если некоторая стратегия s* исключается как строго доминируемая, то по определению существует такая стратегия s', что для любого набора ранее не исключенных стратегий остальных игроков s, выполняется неравенство.

Поскольку ни одна из стратегий из s*₍ не была к этому моменту исключена, то из неравенства (2.2) следует выполнение неравенства.

В то же время, так как (s', s*,) — равновесие по Нэшу, то из неравенства (2.1) следует выполнение неравенства.

Неравенство (2.3) противоречит неравенству (2.4), следовательно, наше исходное предположение было неверным. Что и требовалось доказать. ?

Утверждение 2.2. Если в игре единственный профиль чистых стратегий s' = (s', s^,…, s') остается после последовательного исключения строго доминируемых стратегий, то он образует единственное равновесие по Нэшу в чистых стратегиях в данной игре.

Доказательство. Будем доказывать данное утверждение для конечной игры. Согласно утверждению 2.1 ни одна из стратегий, образующих равновесный по Нэшу профиль, не может быть исключена при последовательном исключении строго доминируемых стратегий. Следовательно, если в игре остается единственный профиль стратегий, то игра либо имеет единственное равновесие по Нэшу, либо не имеет равновесия по Нэшу. Осталось показать, что оставшийся профиль стратегий является равновесием по Нэшу.

Доказательство этого снова проведем от противного.

Пусть в результате последовательного исключения строго доминируемых стратегий в игре остался единственный профиль стратегий s = (s, s ,),.

который нс является равновесием по Нэшу. Тогда по определению для некоторого z'-ro игрока должна найтись стратегия s', для которой выполняется неравенство.

Поскольку .V — единственный не исключенный профиль стратегий, стратегия s' была исключена на некотором шаге. Это означает, что нашлась другая стратегия s", такая что для всех оставшихся к тому моменту наборов s__f выполнялось неравенство.

Из неравенства (2.6) следует выполнение неравенства.

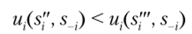
поскольку ни одна из стратегий, составляющихне была исключена.

Теперь возможны два варианта. Или s" = 5,-, тогда неравенство (2.5) противоречит неравенству (2.7), и теорема доказана; или 5," Ф s, тогда существует еще одна стратегия s'", такая что.

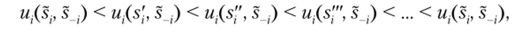
для всех оставшихся к тому моменту наборов стратегий s, а значит, и для набора .§ ;• Опять возможны две ситуации: s'" = s_t, или s'" Ф s_r Повторяя данное рассуждение, приходим к цепочке неравенств.

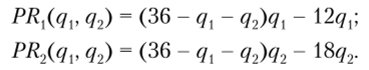
которая указывает на возникающее противоречие (последнее неравенство следует из того, что, но условию, после последовательного исключения строго доминируемых стратегий остался единственный профиль стратегий и игра конечна). Следовательно, наше исходное предположение было неверным. Что и требовалось доказать. ?

Утверждение 2.2 говорит о том, что равновесие по доминированию всегда является равновесием по Нэшу. Как очевидно из примеров 2.4 и 2.6, равновесие по Нэшу необязательно является равновесием по доминированию. Таким образом, концепция равновесия, но Нэшу позволяет получить решение для более широкого класса игр.

Рассмотрим нахождение равновесия по Нэшу для игр, не являющихся конечными, на примере двух базовых моделей дуополии.

Пример 2.7 (дуополия Курно). Две фирмы одновременно и независимо выбирают объем производства и ц₂ на рынке, характеризующемся обратной функцией спроса Р = 36 — Q, где Р — рыночная цена; Q = = ц_х + ц_г — суммарный объем продаж. Издержки первой фирмы имеют вид TC^q^) = 12q_v издержки второй фирмы — TC₂(q₂) = 18q₂. Фирмы максимизируют 11рибыль.

В экономических приложениях часто бывает удобно использовать принятые в конкретной модели обозначения, а не пользоваться общими для теории игр. Поэтому будем обозначать через с/, и q₂ стратегии игроков, множества возможных стратегий (неотрицательные объемы производства) соответственно Q, = Q, = [0; +°°), функции выигрыша¹ (прибыли):

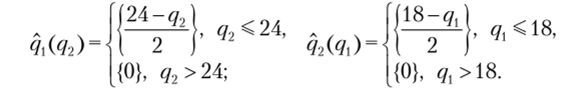
Найдем отображение наилучшего ответа для каждого игрока. В микроэкономике это отображение обычно называют линией реакции. Легко заметить, что функция выигрыша каждого из игроков при фиксированной стратегии другого игрока — парабола с ветвями вниз. Тогда максимум при ограничении неотрицательности будет достигаться в вершине, если вершине соответствует неотрицательное значение объема, или в нуле, если вершина лежит в отрицательной области. Следовательно, имеем.

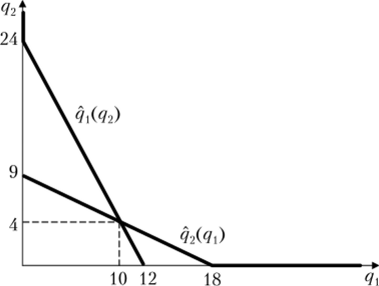
Удобно поступить по аналогии с конечными играми и изобразить полученные отображения графически в пространстве профилей стратегий (рис. 2.1).

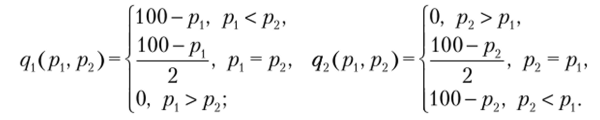
Рис. 2.1. Отображения наилучшего ответа в дуополии Курно.

Точка пересечения (10,4) соответствует равновесию по Нэшу. Отметим, что при достаточно большой разнице в издержках в модели возможно решение, когда одна из фирм ничего не производит. В этом случае отображения наилучшего ответа пересекутся на одной из осей.

Пример 2.8 (дуополия Бертрана). Две фирмы одновременно и независимо выбирают цены продукции р_{ и р₂ на рынке, характеризующемся функцией спроса Q = 100 — Р, где Р — наименьшая из двух цен. Потребители покупают весь объем спроса у фирмы, предложившей наименьшую цену, если такая фирма одна, и покупают у каждой фирмы половину объема спроса, если цены, предложенные фирмами, равны. Издержки первой фирмы имеют вид TC_{(q_{) = 20с/, издержки второй фирмы имеют вид TC₂(q₂) = 20<7₂. Фирмы максимизируют прибыль.

' Случай, когда суммарный объем превышает 36, мы не будем отдельно рассматривать. Несложно показать, что равновесие по Нэшу в этой ситуации возникнуть не может.

Здесь р_у и р₂ — стратегии игроков, а множества возможных стратегий ограничим для удобства записи и нс ограничивая общности решения интервалом Ру = Р₂ = [0, 100]. Объем продаж каждой из фирм определяется функциями.

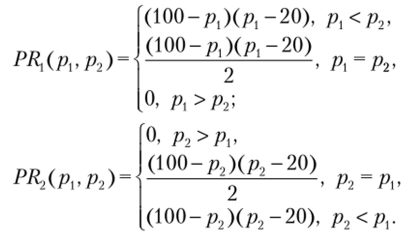
Функции выигрыша (прибыли):

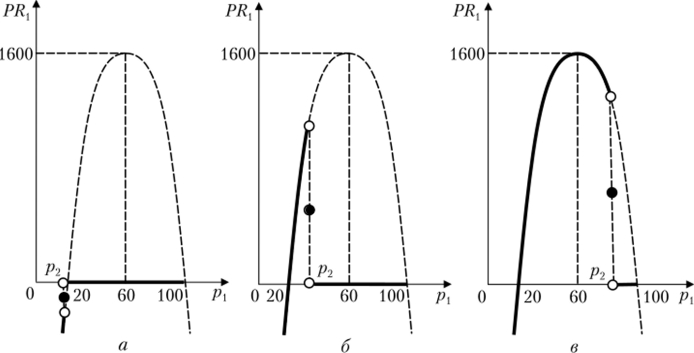
Функция прибыли каждой из фирм от собственной цены при фиксированной цене конкурента имеет три участка:

• • при ценах ниже конкурента — это парабола с ветвями вниз;
• • при цене, равной цене конкурента, — точка на параболе с ветвями вниз;
• • при ценах выше цены конкурента функция совпадает с осью абсцисс. В зависимости от цены конкурента график функции может выглядеть

различным образом. Рассмотрим три возможных случая для первой фирмы (рис. 2.2).

В случае, когда цена конкурента ниже 20 (издержек на единицу), прибыль максимальна и равна нулю при любой цене выше конкурента. При цене конкурента от 20 до 60 (цена 60 соответствует решению монополиста).

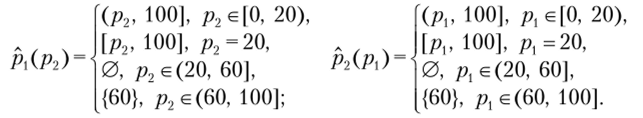
Рис. 2.2. Прибыль фирмы в дуополии Бертрана прибыль не достигает максимума ни при какой цене. Если цена конкурента выше 60, то максимум прибыли достигается при цене 60. Остановимся подробнее на случае, когда максимум прибыли не достигается. В ряде учебников, но микроэкономике для этого случая предлагается для максимизации прибыли устанавливать цену «чуть ниже», чем у конкурента. Но в случае непрерывных цен это «чуть ниже» нс определено, а если цены рассматриваются как дискретные, то решение в целом несколько отличается, в частности в модели появляется еще одно равновесие по Нэшу, в котором обе фирмы устанавливают цены «чуть выше» издержек на единицу.

С учетом граничных случаев, когда цена конкурента равна 20 и 60, получаем следующее отображение наилучшего ответа для первой фирмы и, в силу симметрии, аналогичное для второй фирмы:

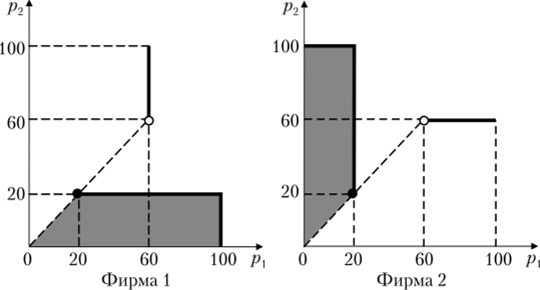
Приведем два отдельных графика для отображений наилучшего ответа каждой из фирм (рис. 2.3).

На рисунке заливкой выделена область в случае неединственного наилучшего ответа, жирной линией обозначены границы, включенные в область. Совмещая два отображения, можно заметить, что единственной точкой пересечения является точка (20, 20), следовательно, она составляет единственное равновесие по Нэшу в данной игре. Содержательно можно отметить, что фирмы в данном случае продают продукцию по цепе, равной их предельным издержкам, получая нулевую прибыль. Результат решения существенно зависит от предпосылки об одинаковых и постоянных предельных издержках. Если изменить эти предпосылки, то можно получить модель без равновесия по Нэшу или с множеством равновесий, не все из которых дают нулевую прибыль фирмам.

Отметим любопытное свойство полученного равновесия по Нэшу (20,20). Стратегия назначить цену 20 слабо доминируема для каждой из фирм, например стратегией назначить цену 30. В первом случае фирма получает нулевую прибыль при любой стратегии конкурента, в то время как во втором случае фирма может получить либо нулевую прибыль, либо положитель;

Рис. 23. Отображения наилучшего ответа в дуополии Бертрана ную, если цена конкурента окажется не ниже 30. Таким образом, в данной игре единственное равновесие по Нэшу достигается при применении игроками слабо доминируемых стратегий.

Равновесие по Нэшу является основной концепцией решения в бескоалиционной теории игр. Но почему именно такая концепция представляется логичной, и всегда ли она приводит к удовлетворительному решению?

Если какая-то ситуация, не являющаяся равновесием по Нэшу, претендует на роль решения игры, то возникают сложности согласования поведения игроков с концепцией рациональности. Если игроки, изменив свое поведение, могут увеличить свои выигрыши (а в неравновесной по Нэшу ситуации кто-то из игроков может это сделать), то почему они не изменят свое поведение? Такая аргументация, однако, может быть нс слишком убедительной, ведь мы предполагаем, что игроки в момент выбора собственной стратегии не знают стратегий других игроков и могут иметь неверные ожидания относительно их действий. Возможно, концепция равновесия по Нэшу наиболее убедительна для «опытных» игроков, которые могут достаточно точно прогнозировать действия оппонентов.

В то же время не любое равновесие по Нэшу выглядит хорошим решением игры. Часто используемый пример здесь следующий. Пусть N> 3 человек выбирают большинством голосов одну из альтернатив, А или Б. Пусть все предпочитают альтернативу А. Тогда голосование всех за альтернативу Б будет равновесием по Нэшу, потому что один голос в любом случае ничего не решит. Естественно, такое решение игры не выглядит логичным. В примере 2.2 тоже можно указать неожиданные равновесия. Например, равновесие по Нэшу будет, если первому участнику поставить 0, а второму участнику — v_l + 1. Поэтому выбор из равновесий, если их множество, представляется актуальной и до конца нс решенной задачей. Для двух приведенных выше примеров правилом выбора может быть, например, такое: если в игре есть равновесие в слабо доминирующих стратегиях, то нужно выбрать его. Но это лишь частный случай. К тому же для игры с двойной матрицей выигрышей вроде следующей¹ указанное правило уже не кажется бесспорным:

Здесь есть равновесие в слабо доминирующих стратегиях (В, Л), но оно не кажется лучшим предсказанием, чем равновесие (II, II).

Общего правила для произвольных игр пока не выработано. В динамических играх, которые мы рассмотрим в следующих главах, выбор «хороших» равновесий будет важной задачей.

До этого момента мы рассматривали лишь выбор решения среди равновесий по Нэшу. Некоторые игры наводят на мысль, что и единственное равновесие может не быть убедительным решением игры. Рассмотрим следующий пример биматричной игры (но мотивам примера Данилова^[5][6]):

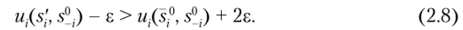
Профиль стратегий (Н, П) составляет единственное равновесие по Нэшу в данной игре. Но заметим: чтобы выбрать П, второй игрок должен быть уверен, что первый игрок не выберет В. А ведь выигрыш первого игрока одинаков при выборе II вторым игроком. К тому же, выбрав В, первый игрок может не бояться, что второй игрок выберет Л. Возможно, рациональный второй игрок задумается о выборе стратегии Ц.

Второй вопрос, па который пока не найдено какого-то однозначного ответа: как игроки приходят к равновесию по Нэшу?

Идеальный теоретический сценарий здесь такой. Игроки независимо друг от друга формируют ожидания относительно действий других игроков, а затем выбирают действия, которые максимизируют их выигрыш при заданных ожиданиях. Если при этом ожидания соответствуют действиям, реально выбранным игроками, то получаем равновесие по Нэшу. Такая схема рассуждений позволяет назвать равновесие по Нэшу ситуацией с самореализующимися ожиданиями. Но откуда берутся сами ожидания? И какое именно из равновесий по Нэшу, если их несколько, будет выбрано в результате описанного процесса? В рамках рассмотренного сценария эти вопросы остаются без ответа.

Другой подход предполагает наличие обучения игроков. Игроки либо теоретически изучают, как следует играть в данной игре (представьте себе студентов экономического факультета), либо имеют опыт схожего взаимодействия (например, опытный работник приходит в новый коллектив), что позволяет им правильно сформировать ожидания и выбрать оптимальное поведение. Этот сценарий позволяет объяснить формирование ожиданий, но он, во-первых, сокращает область применения игровых моделей только до стандартных, изучаемых и часто встречающихся ситуаций взаимодействия, а во-вторых, может приводить к тому, что не разграничиваются ситуации однократного и повторяющегося взаимодействия, а последние существенно отличаются с точки зрения стратегий и методов решения в рамках теории игр, о чем подробнее будет сказано в гл. 4.

Третий сценарий состоит в том, что существуют предварительная договоренность между игроками, или обычаи, или законы, или указания третьих лиц, которые регламентируют взаимодействие игроков. При этом договоренности или указания могут быть необязательны к исполнению, но если рекомендуется сыграть равновесие по Нэшу, то ни у кого из игроков не возникает желания (в одиночку) отклониться от предписанного поведения. Понятно, что такой сценарий возможен не в любой ситуации. Кроме того, сам процесс формирования договоренности или привлечения третьих лиц может стать частью игры.

Наконец, третий естественный вопрос, который возникает при изучении концепции равновесия по Нэшу, следующий: есть ли эмпирические свидетельства того, что реальные игроки обычно выбирают равновесные стратегии? Здесь снова чрезвычайно сложно дать краткий и однозначный ответ. При этом характер возникающих проблем больше соответствует тематике экспериментальной экономики. Поэтому ограничимся рекомендацией обратиться к специализированной литературе, например, книге [7], где отлично разобраны вопросы методологии экспериментов и представлен ряд результатов.

Существуют игры, которые не имеют равновесия в чистых стратегиях (см. пример 3.1), поэтому возникает вопрос: какие условия являются достаточными для существования такого равновесия? Сформулируем и докажем утверждение о существовании равновесия по Нэшу в чистых стратегиях в играх, не являющихся конечными.

Утверждение 2.3. Если множества стратегий каждого из игроков S_t являются непустыми выпуклыми компактами в евклидовом пространстве, а функция выигрыша каждого игрока и- непрерывна по s и квазивогнута по 5, то в игре существует равновесие по Нэшу в чистых стратегиях.

Доказательство. Напомним формулировку теоремы Какутаии, которую мы будем использвать при доказательстве. Пусть X — непустое выпуклое компактное множество в Rⁿ, X* — множество его подмножеств и/ — такое полунепрерывное сверху отображение из X в X*, что для каждой точки х е X множество f (x) непусто, замкнуто и выпукло. Тогда отображение / имеет неподвижную точку.

Идея доказательства нашего утверждения состоит в построении отображения, удовлетворяющего условиям теоремы Какутани. Для этого несколько переопределим отображение наилучшего ответа. Будем, чисто технически, считать, что наилучший ответ зависит не только от стратегий других игроков, но и от собственной стратегии игрока s_y(s). С изменением собственной стратегии игрока при фиксированных стратегиях остальных игроков наилучший ответ, конечно же, меняться не будет. Теперь введем обозначение для отображения наилучшего ответа для всех игроков как декартова произведения s (s) = s,(s) х s₂(s) х … х s_n(s). Это отображение каждому профилю ставит в соответствие множество профилей, в которых каждый игрок наилучшим образом отвечает на стратегии остальных игроков. Неподвижная точка отображения S, т. е. профиль s такой, что s е s (s)> по определению является равновесием по Нэшу. Покажем, что отображение 5 удовлетворяет условиям теоремы Какутани. Проверка каждого условия будет составлять отдельный пункт доказательства.

• 1. Покажем, что множество S всех профилей — выпуклый компакт. Так как, но условию утверждения множества стратегий каждого из игроков S, являются непустыми выпуклыми компактами, то и декартово произведение S = S_t X S₂ X … х S_n является выпуклым компактом.
• 2. Отображение s имеет непустые образы. По теореме Вейерштрасса непрерывная функция и- достигает на замкнутом ограниченном множестве 5, своего максимального значения. Следовательно, s имеет непустые образы.
• 3. Образы отображения s замкнуты и выпуклы. Так как функция выигрыша каждого игрока u_t квазивогнута по s_if то по свойству квазивогнутой функции множество $. = {s. | u_t(s_i9 s .) > k} при фиксированных s .и k замкнуто при замкнутой области определения и выпукло, если не пусто. Так как это верно для любого k, то верно и то, что множество 5. = {5/1 u_t(s', 5 ,) > maxw.(s., s .)}

s, eS_i

выпукло. Но тогда и декартово произведение 5(5) = s_x(s) х s₂ (S) х … X s_n СS) замкнуто и выпукло.

4. Покажем, что отображение § полунепрерывно сверху. Используем условие непрерывности функции и, по s. Доказывать будем от противного. Предположим, что отображение § нс является полунепрерывным сверху. Тогда найдутся последовательности профилей стратегий s^m и s^m, где т — номер элемента последовательности, такие что для любого т s'" е S, s^m е s (s'"), lim s'" = s° е S, но lim s'" = s° g lim s (s'"). Это означает, что найдется иг;

т~* оо т—> /и —? оо рок, для которого стратегия s_f° не является наилучшим ответом на s⁰, т. е. найдется стратегия s' такая, что и,(s', s⁰,) > u,(s] s°_;). Тогда можно найти такое е > 0, чтобы выполнялось m,(s/, s⁰,) > m,(s_;°, s⁰,) + Зе, откуда.

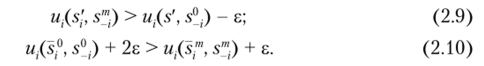
Поскольку по условию функция м, непрерывна, lim s^m = s°, lim s'" = s°,.

m * oo m —* oo.

при достаточно большом m верно.

Объединяя неравенства (2.8)—(2.10) в одну цепочку, получим.

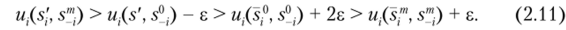
Из соотношений (2.11) следует, что u,(s', s'") > m,(s/", s'") + s, но это противоречит условию s'" е s (s" '), так как s' дает строго больший выигрыш, чем s/", в ответ на s" '. Пришли к противоречию. Следовательно, наша исходная предпосылка, что отображение s не является полунепрерывным сверху, была неверной.

Мы показали, что отображение S удовлетворяет всем условиям теоремы Какутани, а значит, имеет неподвижную точку. Данная неподвижная точка является равновесием по Нэшу. Утверждение 2.3 доказано. ?

Утверждение 2.3, в частности, гарантирует существование равновесия по Нэшу в примере 2.7, но не в примере 2.8, где функции выигрыша игроков разрывны.

В экономике обобщения утверждения 2.3 используются для доказательства существования решения в моделях общего экономического равновесия.

• [1] Строго говоря, там используется модификация аукциона второй цены — обобщенныйаукцион второй цены, так как продается сразу несколько рекламных позиций.
• [2] Пример заимствован из работы [10].
• [3] Джон Форбс Нэш (1928—2015) — американский математик, нобелевский лауреат поэкономике (1994), внесший серьезный вклад в развитие теории игр.
• [4] См. работу [9].
• [5] ' Пример из работы [2|.
• [6] См. работу [2 ].