Табличный метод исчисления
Пусть состояние формулы определяется интерпретацией / = {(S/T), (Л/Т), (В/Т)}. Тогда вычисление формулы в этой интерпретации будет вычислятся по следующей схеме: Для логической формулы Q = (S & (Л v В)) может быть построено следующее дерево синтаксического разбора, в котором определен порядок применения операций: Где Q, В, A, S — переменные (char S), принимающие значения из {Т, F) ~ ~ {-1… Читать ещё >
Табличный метод исчисления (реферат, курсовая, диплом, контрольная)
Для вычисления значения истинности высказывания (как в арифметике при вычислении арифметического выражения) для конкретных значений аргументов используется табличный метод, в котором применяются таблицы истинности для связок высказываний.
При вычислении значений составного высказывания, проверке на общезначимость или противоречивость для формулы, включающей N различных высказываний (Л, 5, С,…), формируется и оценивается таблица истинности, включающая 2N наборов значений истинности упорядоченного вектора простых высказываний.
Вычисления выполняются в порядке, заданном скобками, графом вычисления[1][2], графом синтаксического разбора Wff[1].
Для логической формулы Q = (S & (Л v В)) может быть построено следующее дерево синтаксического разбора, в котором определен порядок применения операций:
Вычисление истинности при интерпретации выполняется в обратном порядке и представлено схемой вычислений.
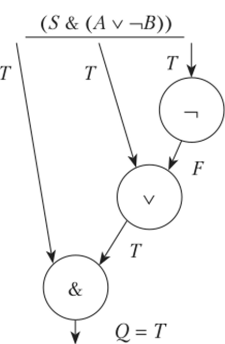
Пусть состояние формулы определяется интерпретацией / = {(S/T), (Л/Т), (В/Т)}. Тогда вычисление формулы в этой интерпретации будет вычислятся по следующей схеме:
Оператор для вычисления значения функции Q (A, В, S) по этой схеме на языке C++ имеет следующий вид:
где Q, В, A, S — переменные (char S), принимающие значения из {Т, F) ~ ~ {-1, ()}; можно использовать поразрядные битовые операции с двоичными кодами.
При значениях истинности входящих в формулу простых высказываний S = А = -пВ = Т, Q= Т формула Q (S, А, В) выполнима.
Для проверки общезначимости и противоречивости формулы требуется перебор из 2ДГ интерпретаций и построение полной таблицы истинности. Объем вычислений пропорционален п2т, где п — число логических операций в формуле; 2т — число двоичных наборов.
Составим таблицу истинности для формулы Q = (-А v В) —" С:
Л. | —Л. | В | -Aw В | мСм | <2(А в, О. |
F | т | F | Т | F | F |
F | т | F | Т | Т | Т |
F | т | Т | Т | F | F |
F | т | Т | Т | Т | Т |
Т | F | F | F | F | Т |
Т | F | F | F | Г | Г |
Т | F | Т | Т | F | F |
Т | F | т | т | Т | Т |
Формула <2(Д В, С) выполнима и не является тавтологией.
- [1] Черноскутов Ю. Ю. Логика. Краткий конспект. СПб.: Проспект, 2013.
- [2] Грэй П. Логика, алгебра и базы данных. М.: Машиностроение, 1989; Лихтарииков Л. М, Сухарева Т. Г. Математическая логика: курс лекций, задачник-практикум и решения. 4-е изд., стер. СПб.: Лань, 2009.
- [3] Черноскутов Ю. Ю. Логика. Краткий конспект. СПб.: Проспект, 2013.