Интерференционные электрофизиологические процессы

В биотелеметрии в основном измеряют интерференционную картину биоэлсктрической активности (ЭЭГ, ЭМГ, ЭКГ, ЭРГ и т. д.), образующейся в результате пространственно-временного суммирования биопотенциалов различных биологических структур. Поскольку в основе интерференционных электрофизиологических процессов лежат ПСП и ПД соответствующих групп определенным образом организованных клеток, то при моделировании этих процессов необходимо использовать информацию о статистике ПСП и ПД.

Учитывая, что на регистрируемый электрофизиологический процесс в точках отведения влияет множество различных факторов (методика отведения, электрические характеристики исследуемой структуры и биосреды между источником информации и точками отведения, помехи и т. д.) и принимая во внимание характер ПСП и ПД, результирующий процесс можно записать в форме.

где а_к — вектор случайных параметров, отражающих влияние различных факторов на форму F (-) отдельных импульсов результирующего интерференционного процесса. Поскольку большинство факторов, влияющих на форму F () и момент возникновения t_k отдельных импульсов электрофизиологического процесса, можно считать независимыми [34, 36, 50, 123, 154], то в стационарной пуассоновской схеме плотность вероятности результирующего процесса можно найти с помощью уравнения (2.72), в котором характеристическая функция.

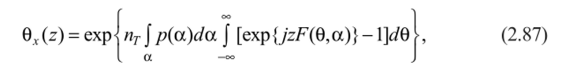
где р (а) — функция распределения вектора случайных параметров а.

Анализ уравнений (2.72) и (2.87) показывает, что плотность вероятности интерференционного электрофизиологического процесса существенно зависит от параметра п_т, характеризующего плотность следования элементарных импульсов, составляющих результирующий процесс, и их формы. Так, если величина п, и средняя длительность импульса т велики настолько, что выполняется условие.

то плотность вероятности р (х) близка к нормальному закону, часто наблюдаемому, например, при поверхностных отведениях ЭМГ и ЭЭГ [44, 45, 143]:

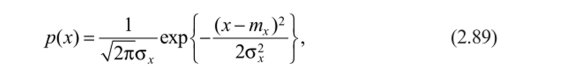
где о]. — дисперсия; т_х — математическое ожидание параметра х.

Если же тп_Т мало, то р (х) существенно отличается от нормального и сильно зависит от формы отдельных импульсов.

В качестве иллюстрации приведенных соотношений определим, например, плотность вероятности интерференционной ЭМ Г. Учитывая, что действие многочисленных факторов сводится к изменению амплитуды А и длительности составляющих т ЭМГ элементарных импульсов [34], положим а = (А, т). Тогда процесс (2.80) можно переписать в форме.

При этом характеристическая функция (2.87) примет вид.

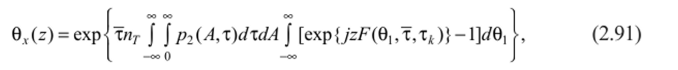
где 0, = (/- t_k) I т, р₂(А, т) — совместная плотность вероятности амплитуды А и длительности т импульса.

Если форму отдельного импульса ЭМГ принять близкой к прямоугольной [45, 105], то с учетом условия нормировки для р₂ = (А, т) уравнение (2.91) примет вид.

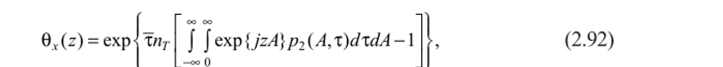
откуда, используя известное разложение.

где 0^(z) — подынтегральное выражение в (2.92), получим согласно (2.72) функцию распределения ЭМГ:

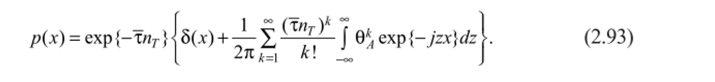
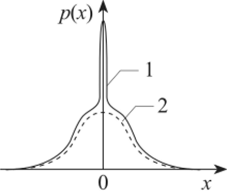
Рис. 2.8.

Функция (2.93) описывает распределение вероятностей процесса пуассоновского типа, хорошо исследованного в литературе [105, 142, 194]. Из (2.93) следует, что при л* = 0 имеет место пик в распределении р (х), что соответствует ненулевой вероятности нулевых значений интерференционной ЭМГ. В частном случае, когда случайными являются только амплитуды элементарных импульсов, причем последние распределены нормально с нулевым средним и дисперсией с_А, выражение (2.93) примет вид.

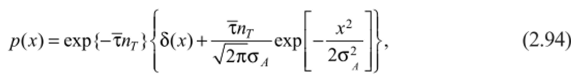
т.е. функция р (х) содержит два слагаемых, соответствующих нормальному распределению при х ф 0 (кривая 2) и пику в форме 8-функции при х = 0 (кривая 1, рис. 2.8). По своей форме функция (2.94) близка к экспериментально наблюдаемому закону распределения [44, 45] ЭМГ некоторых биологических структур.

Среднее значение, дисперсию, корреляционную и спектральную характеристики интерференционного электрофизиологического процесса общего вида (2.86) можно найти с помощью известных уравнений.

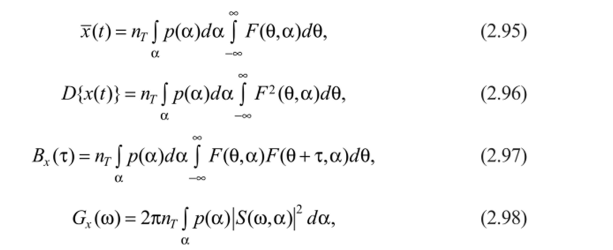
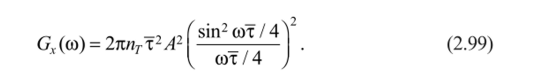
(На рис. 2.9 1 — теоретическая (2.99); 2 — экспериментальная кривая.).

Для ряда электрофизиологических процессов (ЭЭГ, ЭМГ и др.) в силу симметрии составляющих импульсов среднее значение обычно равняется нулю. Спектральная характеристика интерференционного процесса в основном определяется формой элементарного импульса F (). В частности, для примера ЭМГ, рассмотренного выше, спектральная характеристика (рис. 2.9).

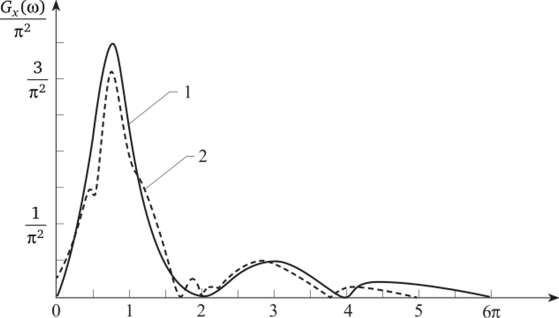
Рис. 2.9.

Таким образом, густота п_т, средняя длительность т и амплитуда А элементарного импульса определяют только общий уровень энергетического спектра ЭМГ.

В ряде электрофизиологических исследований представляют интерес лишь некоторые параметры электрофизиологического процесса: амплитуды отдельных импульсов, их длительность, моменты появления и др. [110]. Так, в норме моменты возникновения комплекса PQRST ЭКГ подчиняются либо нормальному закону, либо закону.

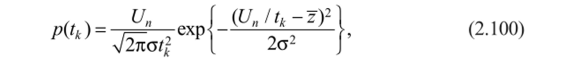
где U_n — разность потенциалов между порогом возбуждения и уровнем покоя клеток водителя ритма; z — скорость деполяризации постсинаптической мембраны; а² — дисперсия процесса, т. е. в данном случае кривая p (t_k) ассимстрична относительно среднего значения 1 более вероятными оказываются короткие R-R интервалы. Если скорость деполяризации изменяется по нелиней ному закону, то распределение межимпульсных интервалов будет отличаться от (2.100); например, при экспоненциальной зависимости это распределение будет подчиняться логарифмически нормальному закону.

Огибающая ЭЭГ в ряде важных случаев распределена по закону Релея [34]:

Отдельные волны, возникающие в интерференционной картине ЭЭГ (о, р, у, 8, 0 — ритмы), в первом приближении могут быть описаны моделью узкополосного случайного процесса вида.

u (t) — A (t)cos®,/ + ?(/)sinoy = f/(/)cos[o.),/ + cp (/)], (2.102).

где U (t) = yjA²(t) + В² (t) — огибающая; cp (/) = arctg[5(/) / A (/)] — случайная фаза отдельного ритма ЭЭГ частоты ю₀. Причем U (t) и ср (/) — случайные медленно меняющиеся функции.

Корреляционные и спектральные характеристики процесса типа (2.102) определяются известными соотношениями [160]:

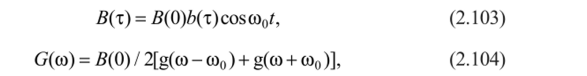
где Ь{т) — нормированная корреляционная функция процессов.

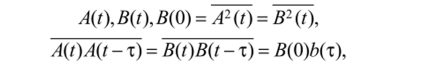
" (о)) — спектральная интенсивность процессов A (t) и B (t) (преобразование Фурье от Ь (т)).

Принимая во внимание интегрирующие свойства тканей (см. § 2.6), для Ь (т) можно принять следующую аппроксимацию:

при этом (2.104) примет вид.

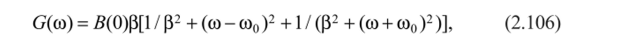
часто наблюдаемый в реальном эксперименте [143].