Удар по телу, вращающемуся вокруг оси. 
Центр удара

Пусть тело вращается вокруг неподвижной оси Ох_} и Ох, х₂х₃ — система координат, связанная с телом (см. § 5.9, рис. 42). Если в момент времени / = 0 тело испытывает удар Р6(г), приложенный в точке D с координатами (</, d₂, d₂) = d, то в правых частях уравнений (5.9.2) следует добавить момент ударного импульса d х Р5(/) и ударный импульс Р5(г) соответственно. Кроме того, реакции связей в точках О и Р, вообще говоря, будут иметь импульсный характер. Проинтегрируем уравнения (5.9.2) по времени оте до е, перейдем к пределу при е -" 0 и получим уравнения удара.

где R₀ — ударные реакции связей. Поскольку R^= (Х_]Р, X_2h 0), R₀ = (X_w, Х_20л Х_ю), Дш = Д<�ое₃ (е₃ — орт оси 0х₃), то из шести уравнений (6.1) определяются шесть неизвестных величин.

Найдем условия, при которых во время удара не возникают ударные реакции связей, т. е. R^=R_o = 0. Из второго уравнения (6.1) при R_f = R₀= 0 следует, что импульс Р ортогонален плоскости, содержащей векторы Дса, р_с Примем эту плоскость в качестве плоскости 0х, х₃. Тогда р_с= (х, 0, х₃) и Р = Л/Да>х, е₂. Из первого уравнения (6.1) при R^= 0 следует, что вектор d может быть задан с точностью до произвольного слагаемого вида Хе₂. Назовем центром удара точку, удовлетворяющую уравнению /Лео = d х Р, когда d = (d_h 0, </<sub>3). Последнее уравнение эквивалентно трем скалярным уравнениям.

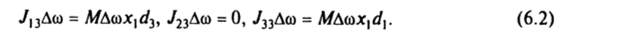
Условия (6.2) будут выполнены при произвольном Д<�о * 0, когда.

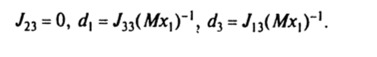
В заключение сформулируем условия, при которых не возни* кают ударные реакции связей, когда вращающееся вокруг оси Ох_} тело подвергается удару внешних сил: если центр масс тела расположен в плоскости Ох|Х₃, то центробежный момент инерции должен быть равен нулю; произвольный по величине удар должен быть направлен по оси Ох₂. а его линия действия должна проходить через центр удара.

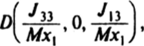
где X, — координата центра масс. Описанная ситуация возможна, если центр масс тела не лежит на оси вращения (х, * 0).