Классификация плоских механизмов

В основу классификации положено требование единства методики кинематического и силового анализа механизмов. Этому требованию соответствует структурная классификация механизмов, разработанная профессором Л. В. Ассуром в 1916 году и получившая дальнейшее развитие в трудах академика И. И. Артоболевского. Основная идея Л. В. Ассура состоит в том, что любой механизм может быть создан путем присоединения к начальному звену (или начальным звеньям) и стойке кинематических цепей нулевой подвижности, называемых структурными группами (группами Ассура) [3, с. 13].

По классификации И. И. Артоболевского начальное звено и стойка, образующие кинематическую пару пятого класса, являются механизмом 1-го класса (рис. 3.9). Группой Ассура называется кинематическая цепь, степень подвижности которой после присоединения ее свободных элементов к стойке равна нулю при условии, что она не распадается на более простые группы Ассура.

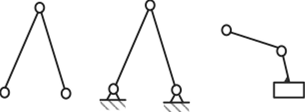
Рис. 3.10.

На рис. 3.10, а, б, в представлены простейшие группы, состоящие из двух звеньев. Для них IV = Ъп — 2р₅ = 3 • 2 — 2 • 3 = 0, если свободные элементы присоединить к стойке (рис. 3.10, б). В этом случае группа превращается в ферму.

Для групп с парами только 5-го класса.

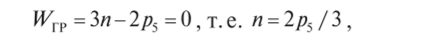
при этом п и р₅ — целые числа.

На рис. 3.11 представлены механизмы, образованные путем присоединения к механизму 1-го класса и стойке групп Ассура.

Рис. 3.11.

Поскольку степень подвижности групп Ассура равна нулю, степень подвижности механизма равна числу начальных (ведущих звеньев) или числу механизмов 1-го класса. Например, для механизмов, представленных на рис. 3.11, а, б, степень подвижности W= +0=1. При двух механизмах первого класса и одной присоединенной группе (рис. 3.11,6?) степень подвижности механизма равна IV= + 0+1 = 2.

Класс группы определяется наивысшим по классу контуром, входящим в ее состав.

Класс контура равен числу кинематических пар, входящих в замкнутый контур.

Порядок группы равен числу свободных элементов кинематических пар, которыми группа присоединяется к механизму.

На рис. 3.12 представлены группы Ассура различных классов. Звеньями этих групп образованы контуры:

в группе АВС (см. рис 3.12, а) — контур А В или ВС содержит 2 кинематические пары, следовательно, является контуром 2-го класса;

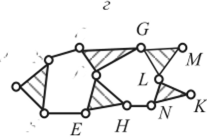
в группе ABCDEF(рис. 3.12, б) — контур ВСЕ 3-го класса; в группе ABGDEF(рис. 3.12, в) — контур BCEF4-го класса; в группе ABCDEFGHKLMN (рис 3.12, г) можно отыскать два контура 5-го класса BCDEF и DGLNH, которые содержат по 5 кинематических пар.

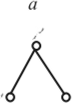
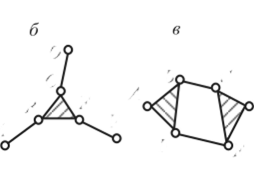
Рис. 3.12.

Сочетание чисел п = 2 и р₅ = 3 характерно для структурных групп 2-го класса, сочетание п = 4, р₅ = 6 при наличии трех поводков и одного базисного звена — для групп 3-го класса.

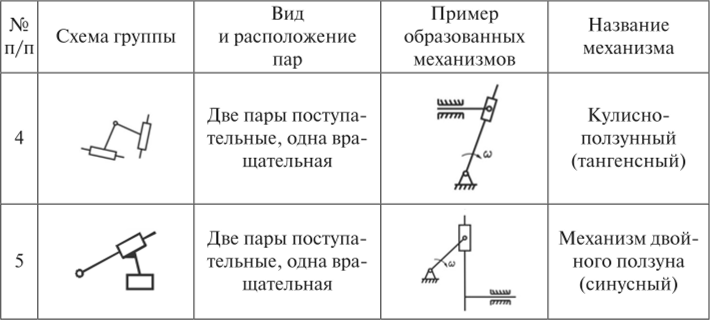
В практике синтеза механизмов наибольшее распространение получили группы второго класса. В зависимости от числа и взаимного расположения вращательных и поступательных кинематических пар различают 5 видов структурных групп 2-го класса (табл. 3.2).

Таблица 3.2

Виды групп Ассура второго класса.

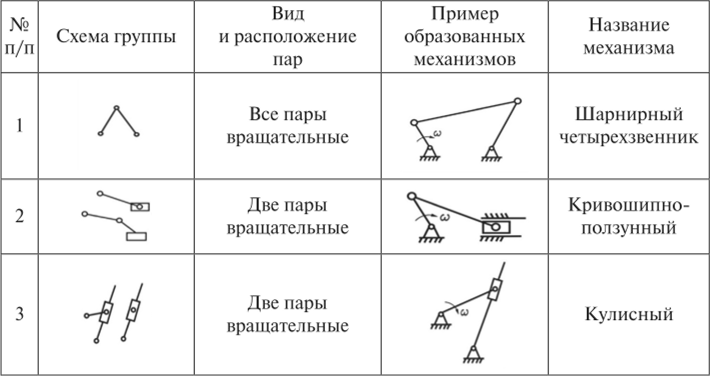
Окончание табл. 3.2.