Вариационный принцип гамильтона-остроградского в конфигурационном и фазовом пространствах

Траектории, описывающие движения механических систем в расширенном конфигурационном и фазовом пространствах, обладают замечательным свойством — они являются экстремалями некоторой вариационной задачи, доставляют стационарные значения функционалу действие.

Рассмотрим постановку вариационной задачи в расширенном конфигурационном пространстве R" *', точками которого являются наборы (q, (). Пусть кривая у" = {(q, t): q е R t e [/", /,), q = q (f)}, где q (/) является решением уравнений Лагранжа второго рода:

Таким образом, у₀ — действительная траектория (рис. 45). Рассмотрим класс окольных траекторий {у}, где у = {(q + 5q, /): q + 5q е e R", l e [f₀, /,], 5q (/₀)= 8q (/,) = 0). Вариация 8q (/) — произвольная функция из класса С¹, обращающаяся в нуль на концах отрезка [Jq, /J.

0.2.1. Отображение класса окольных траекторий {у} в Л¹, определяемое равенством.

называется функционалом действие по Гамильтону.

0.2.2. Вариацией функционала действие называется выражение.

Вариационный принцип Гамильтона—Остроградского формулируется следующим образом: функционал действие по Гамильтону принимает стационарное значение на действительной траектории в классе окольных траекторий, т е. вариация 5.5[у₀] = 0.

А Первая вариация функционала Sy при у = у₀ согласно определению равна.

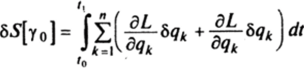
и после интегрирования по частям принимает вид.

Внеинтетральный член в выражении (2.3) обрашается в нуль, так как bq_k(t₀) = bq_k(t_y) = 0, к — 1… л, а выражение в квадратных скобках под знаком интеграла равно нулю, поскольку у₀ — действительная траектория, удовлетворяющая уравнениям Лагранжа (2.1). Следовательно, вариация 55(у₀) = 0. ?

Верно и обратное утверждение: если вариация 65(у*) = 0, где у* принадлежит классу окольных траекторий, то у* = у₀ — действительная траектория. Справедливость этого утверждения следует из выражения первой вариации (2.3) и основной леммы вариационного исчисления. В данном случае из равенства нулю первой вариации.

и независимости вариаций 6<7*(/) = 0, к — 1, …, ливость уравнений Лагранжа второго рода.

л, вытекает справед;

когда q_k = q_k*(t), к= 1… л. Это и означает, что у* — действительная траектория движения механической системы.

3.1. В случае неконсервативной системы нельзя указать функционал, стационарное значение которого достигалось на действительной траектории. Однако в этом случае эквивалентны следующие утверждения:

где q (/) — действительная траектория. Первое из вышеуказанных утверждений составляет содержание вариационного принципа Гамильтона—Остроградского для неконсервативных систем.

3.2. Можно показать, что стационарное значение функционала действие является минимумом, если разность — /₀ достаточно мала. Это обстоятельство связано с другим названием обсуждаемого принципа — принципа наименьшего действия Гамильтона— Остро граде ко го.

Вариационную задачу, рассмотренную выше, можно сформулировать в расширенном фазовом пространстве, что оказывается важным при рассмотрении вопросов интегрируемости канонических уравнений Гамильтона. Обозначим через Г = {(р + 6р. q + 8q, I): р, q, 6р. 6q е R", te [г₀, /,]. 5q (/₀)= 8q (/|) = 0} кривую в расширенном фазовом пространстве и пусть при 8p = 8q = 0 кривая Г₀ является решением системы канонических уравнений Гамильтона.

Все функции времени принадлежат классу С¹. Таким образом, определено семейство окольных траекторий {Г}, которому принадлежит действительная траектория Г₀ (рис. 46). Функционал действие с учетом связи между функциями Лагранжа и Гамильтона принимает вид.

Здесь буквы р, q употреблены для краткости вместо букв р + 8р, q + 8q. Вычисляя вариацию функционала 5[Г] на действительной траектории, получим.

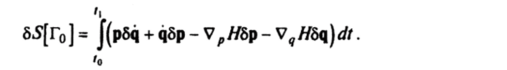
Интегрируя по частям с учетом граничных условий, найдем.

Отсюда следует, что вариация 85|Г₀1 = 0, если р (/), q (f) удовлетворяют каноническим уравнениям Гамильтона (2.4), и. наоборот, из условия независимости вариаций 8р (г), 6q (/) следуют уравнения (2.4) согласно основной лемме вариационного исчисления.

Таким образом, доказана справедливость принципа наименьшего действия в фазовом пространстве системы: функционал действие 5[Г], заданный на пространстве окольных траекторий (Г|. принимает стационарное значение на действительной траектории, т. е. 85[Г₀1 = 0.

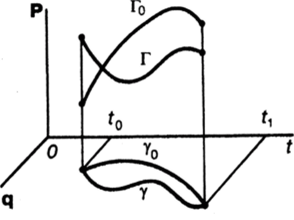
Рис. 46 Рис. 47.

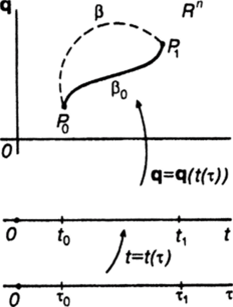
• 3.3. При построении функционала (2.5) использовалась связь между функциями Лагранжа и Гамильтона и преобразование Лежандра р *= V^?. В дальнейшем переменные р, q рассматривались как независимые и из стационарности функционала действие были получены обратное преобразование Лежандра q = V_pH и динамическое уравнение р = -У_ЯН .
• 3.4. Класс окольных траекторий может быть сужен путем введения условий бр (/₀)= бр (Г|) = 0. Семейство окольных траекторий в этом случае обозначим {Г*}, Г* = {(р + 8р, q + 6q, t): р, q, Sp, 6q e Rⁿ, 5q (/,)= 6p (/,) = 0, /' = 0, 1}. Легко проверить, что стационарное значение функционала действие 5[Г*| на этом пространстве окольных траекторий с закрепленными концами также достигается на действительном движении механической системы. Это утверждение составляет принцип наименьшего действия в форме Пуанкаре.