Предельная ошибка репрезентативности выборки

В предыдущем параграфе мы рассмотрели пример выборочного обследования рабочих с целью определения их среднего дохода. Выполненные расчеты позволяют утверждать, что на анализируемом предприятии (в генеральной совокупности) доля рабочих со средним доходом больше 7 тыс. руб. будет находиться в интервале.

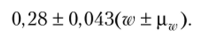
Это записывается так: 0,237 < р < 0,323 и читается: на всем предприятии удельный вес рабочих, имеющих месячный доход более 7 тыс. руб., находится в пределах от 23,7 до 32,3%.

В соответствии с выполненными расчетами можно также утверждать, что средний доход одного рабочего во всей генеральной совокупности будет находиться в интервале.

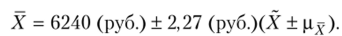
Это означает, что на всем предприятии средний доход рабочих за месяц находится в интервале от 6237,73 до 6242,27 руб. и записывается так: 6237,73 < X < 6242,27.

Полученные таким образом характеристики генеральной совокупности являются вероятностными, т. е. могут быть гарантированы лишь с определенной степенью вероятности. Конкретно в данном случае — с вероятностью, равной 0,683. Что означает, что в 683 случаях из 1000 показатели генеральной совокупности будут находиться в определенных нами интервалах. В остальных 317 случаях они могут выйти за эти пределы. Определенные нами интервалы называются доверительными.

Вероятность суждения можно повысить, если увеличить длину интервала. Общая формула доверительного интервала записывается следующим образом:

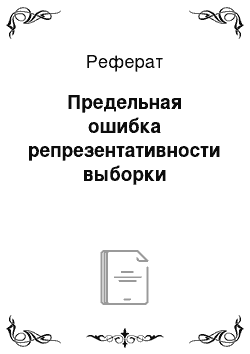
• • при изучении доли альтернативного признака: р = w ± ?|Л_а,;
• • при изучении средней величины количественного признака: X = X ±

Множитель t в этих формулах называется коэффициентом доверия и определяется в зависимости от того, с какой вероятностью гарантируются результаты выборочного обследования. В основе определения этого коэффициента лежит функция, обоснованная русским математиком А. М. Ляпуновым. На практике пользуются готовыми таблицами этой функции «Значения интеграла вероятностей нормального закона распределения». В такой таблице даны значения t при разных уровнях вероятности.

Величина называется предельной ошибкой выборки, и значение ее зависит от средней ошибки выборки и выбранного уровня вероятности:

В экономических исследованиях ограничиваются значениями ?, не превышающими двух-трех единиц, чему соответствует значение вероятности от 0,954 до 0,997. В табл. 6.1 приведены некоторые значения t и соответствующие им значения вероятности.

Таблица 6.1

Некоторые значения t и соответствующие им значения вероятности.

Рассчитаем доверительные интервалы для обеих характеристик, определяемых в нашем примере, при вероятности 0,997.

Этой вероятности соответствует t = 2,6. Тогда предельная ошибка выборки в соответствии с формулой (6.6) определится:

• для доли альтернативного признака, такой как 2,6 • 0,043 = 0,112, доверительный интервал будет выглядеть так:

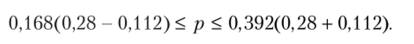
Это означает, что в 997 случаях из 1000 доля рабочих на обследуемом предприятии, имеющих месячный доход больше 7 тыс. руб., будет составлять от 16,8 до 39,2%. Таким образом, увеличение достоверности результатов сопровождалось увеличением длины доверительного интервала с 8,6% (32,3 — 23,7) до 22,4% (39,2 — 16,8);

• для средней величины изучаемого признака, такой как 2,6 • 2,27 = 5Д), доверительный интервал будет выглядеть так: 6234,1(6240 — 5,90) < X < < 6245,9(6240 + 5,90). Таким образом, в 997 случаях из 1000 средний доход рабочих обследуемого предприятия будет находиться в пределах от 6234,1 до 6245,9 руб. В данном случае повышение степени достоверности результата выборки привело к увеличению доверительного интервала с 4,54 до 11,8 руб.

Таким образом, в основе алгоритма расчета показателей генеральной совокупности по характеристикам выборочной совокупности, сформированной, но методу бесиовторного отбора, лежат формулы (6.4) и (6.5). Эти формулы упрощаются при сравнительно небольшом проценте единиц (до 5%), взятых в выборку, и выглядят так же, как в случае повторного отбора (формулы (6.2) и (6.3)).