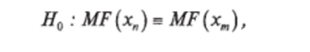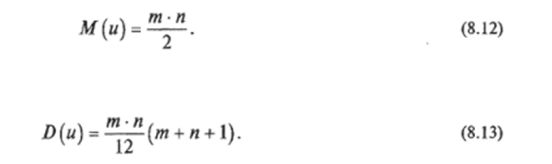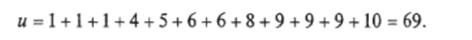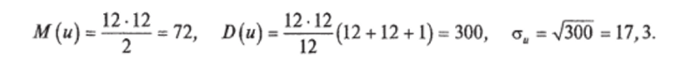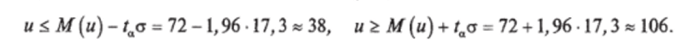Проверка однородности статистического материала и гипотез о законе распределения случайной величины
И дисперсией Пример. Собраны статистические сведения о повреждаемости воздушных ЛЭП (со, отк/год) в двух энергосистемах. Требуется определить, можно ли считать, что между данными о повреждаемости ЛЭП в разных энергосистемах нет систематических расхождений и что они имеют одинаковые систематические погрешности, т. е. нужно проверить нулевую гипотезу Hq. Пусть помимо выборки х, х2, …f хп имеются… Читать ещё >
Проверка однородности статистического материала и гипотез о законе распределения случайной величины (реферат, курсовая, диплом, контрольная)
Проверка однородности статистического материала
Для точного определения ПН, видов законов распределения наработки на отказ и других СВ необходимо объединять статистические данные, собранные на различных объектах промышленных предприятий и энергосистем. В связи с этим возникает задача проверки однородности статистического материала.
Пусть помимо выборки х, х2, …f хп имеются также взаимно независимые величины xf, xj, …, х‘т) распределенные одинаково и непрерывно, но принадлежащие другой выборке. Объединим эти совокупности, расположив их в порядке возрастания значений х", ххп.т. Обозначим: Gm(x) — функция эмпирического распределения, соответствующая выборке х[, х,2, х'т.
Основная гипотеза Hq, подлежащая проверке, заключается в предположении, что обе выборки извлечены из одной и той же совокупности, а значения функции распределения величин хиУ одинаковы. Эту гипотезу можно выразить тождеством где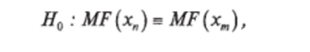 
F{x) — функция эмпирического распределения, построенного на выборке хх, х7, хщ.
Для проверки нулевой гипотезы используется критерий Вилкоксона*, основанный на числе инверсий, под которыми понимается следующее: если какому-либо значению х предшествует некоторый хговорят, что эта пара даст инверсию.
А Гипотеза Н0 отвергается, если сумма инверсий где к — число инвер;
м сий, превосходит выбранную в соответствии с уровнем значимости границу, определяемую из расчета, что при объемах п > 10 и т > 10 выборок число инверсий распределено по нормальному закону с центром.
и дисперсией Пример. Собраны статистические сведения о повреждаемости воздушных ЛЭП (со, отк/год) в двух энергосистемах. Требуется определить, можно ли считать, что между данными о повреждаемости ЛЭП в разных энергосистемах нет систематических расхождений и что они имеют одинаковые систематические погрешности, т. е. нужно проверить нулевую гипотезу Hq.
Энергосистема. | Обозначе; ние. | Месяцы. | |||||||||||
я. | Ф. | м. | а. | м. | и. | и. | а. | с. | о. | н. | д. | ||
X. | 0,8. | 1,9. | 3,0. | 3,5. | 3,8. | 2,5. | 1,7. | 0,9. | 1,0. | 2,3. | з, з. | 3,4. | |
1,4. | 2,1. | 3,1. | 3,6. | 2,7. | 1,8. | 1,1. | 0,2. | 1,6. | 2,8. | 4,0. | 4,7. | ||
Решение. Располагаем исходные данные в общей последовательности, в порядке возрастания повреждаемости:
X? | X. | X. | X. | X'. | х'. | х'. | X. | х/ | X. | х7 | X. |
0,2. | 0,8. | 0,9. | 1,0. | 1,1. | 1,4. | 1,6. | 1,7. | 1,8. | 1,9. | 2,1. | 2,3. |
X | х'. | х/ | X. | х> | X. | X. | X. | х/ | X. | х/ | х' |
2,5. | 2,7. | 2,8. | 3,0. | 3,1. | 3,3. | 3,4. | 3,5. | 3.6. | 3,8. | 4,0. | 4,7. |
Число инверсий для х равно.
По формулам (8.12) и (8.13) находим.
Задавшись уровнем значимости критерия, а = 5%, и учитывая, что обе энергосистемы равноправны, строим критическую область больших по абсолютной величине отклонений. Используя таблицы [73 и др.), получаем значение /5= 1,96.
Критическая область для гипотезы Hq определится как:
Полученное расчетное значение инверсии и = 69 не лежит в критической области, поэтому гипотеза #о не опровергается и нет оснований считать энергосистемы существенно различающимися по аварийности ЛЭП.