Цифровые фильтры. 
Общая теория связи

Цифровым фильтром называют цифровое вычислительное устройство, преобразующее последовательность отсчетов {u (kAt)} = {и_Т} = {wj входного сигнала в последовательность отсчетов {у (kAt)} = {г/_ц} = {у_к} выходного сигнала: [щ] => {у,}.

Пусть последовательность чисел {и_к} — массив отсчетов входного сигнала u (t), взятых с интервалом дискретизации At. Выходным сигналом фильтра будет последовательность отсчетов {у_к}. Для описания реакции цифрового фильтра па входное воздействие в виде дискретной последовательности чисел используют его импульсную характеристику {h{k~t)} = {h_k} = h_k. Из теории цифровых фильтров известно, что импульсная характеристика представляет собой дискретную последовательность чисел, являющуюся его реакцией на «единичный импульс» — дискретизированную дельта-функцию 8(kAt) = 8_к (в цифровом представлении это 1, 0, 0, 0,…):

(1,0, 0, 0,…,…) => {h₀, /г, h₂, h_k) = h_k. Дискретизированную дельта-функцию обозначают как.

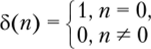
и называют цифровой дельта-фуикцией или функцией Кронекера (рис. 6.17).

Рис. 6.17. Цифровая дельта-функция.

Дискретный сигнал можно разложить в сумму таких функций, сдвинутых во времени. Например, бесконечный сигнал и{п) представим в виде.

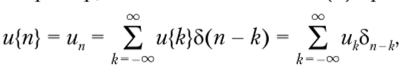
где 5″ — базисные функции, a u{k) — коэффициенты в линейной комбинации.

Если в последней формуле зафиксировать любое п, то получим тождество ип) = ип} х 1, так как все остальные члены суммы обратятся в нуль, поскольку дельта-функция отлична от нуля только в нуле.

Импульсную характеристику h_k цифрового фильтра можно трактовать как результат дискретизации по теореме отсчетов непрерывной импульсной характеристики h (t) соответствующего аналогового линейного фильтра. В дискретных и цифровых фильтрах импульсные характеристики могут иметь конечное и бесконечное число отсчетов (рис. 6.18).

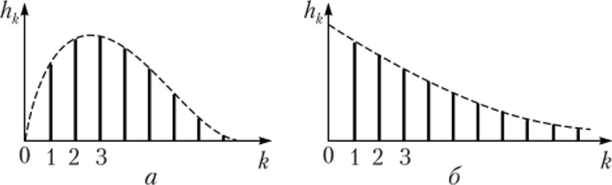
Рис. 6.18. Импульсные характеристики цифровых фильтров с числом отсчетов:

а — конечным; б — бесконечным Оказывается, зная 1г{п} (отклик системы на дельта-функцию), можно вычислить отклик системы на любой входной дискретный сигнал. Действительно, поскольку любой входной сигнал является линейной комбинацией сдвинутых во времени дельта-функций, то выходной сигнал будет той же самой линейной комбинацией сдвинутых во времени функций h{n}. Это следует из линейности системы и ее инвариантности к сдвигу во времени.

Рассмотрим действие цифрового фильтра с простейшими алгоритмом фильтрации и импульсной характеристикой с небольшим числом отсчетов (рис. 6.19). Положим, что входная последовательность {г/Д из четырех единичных отсчетов и₀, u_v щ, и₃ сигнала u (t) подается на вход фильтра с импульсной характеристикой {й_ш}, имеющей отсчеты h_{) = 1,5; h_{ = 1; h₂ = 0,5 (рис. 6.19, а, в). В результате на выходе фильтра возникает последовательность отсчетов {г/Д. При воздействии первого отсчета сигнала щ = 1 на выходе фильтра формируется последовательность откликов, определяемых его импульсной характеристикой. Таких отсчетов будет три: 1,5; 1; 0,5 (рис. 6.19, в). Эта последовательность опишется формулой uji_m.

Воздействие второго отсчета и_х = 1 приведет к появлению на выходе фильтра последовательности еще трех откликов 1,5; 1; 0,5 (рис. 6.19, г), которые аналитически можно выразить как u_xh_m__{.

Рис. 6.19. Цифровая фильтрация:

а — входной сигнал; б — импульсная характеристика; в — е — отклики на 0-й, 1-й, 2-й и 3-й входные отсчеты; ж — выходной сигнал Подобная картина будет иметь место и при отклике цифрового фильтра на воздействие остальных отсчетов входной последовательности (рис. 6.19, д — е). В результате прохождения всего входного сигнала на выходе цифрового фильтра с импульсной характеристикой h_m создастся сумма откликов 1,5; 2,5; 3; 3; 1,5; 0,5 (рис. 6.19, ж). Общее выражение для выходных отсчетов примет вид.

Соотношение (6.30) и определяет алгоритм линейной цифровой фильтрации во временной области. Этот алгоритм показывает, что выходная последовательность представляет собой дискретную свертку входного сигнала с импульсной характеристикой цифрового фильтра. Импульсную характеристику цифрового фильтра h_m называют ядром свертки, а число отсчетов т — длиной ядра свертки.

Полное число выходных отсчетов при этом составляет N = т + k — 1. Отметим очевидное: для физически реализуемых цифровых фильтров коэффициенты h, h ₂,… импульсной характеристики обращаются в нуль.

Системная (передаточная) функция цифрового фильтра. С помощью метода 2-преобразования удается определить важные характеристики цифрового фильтра. Положим, что дискретным входному {u_k} и выходному {у,} сигналам и импульсной характеристике цифрового фильтра {h_k} соответствуют 2-преобразования U (z), Y (z) и H (z). Поскольку выходной сигнал фильтра есть свертка входного сигнала с импульсной характеристикой, то согласно формуле (6.29) 2-преобразованию выходного сигнала отвечает функция.

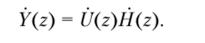
Системная функция, или функция передачи дискретной системы, является отношением 2-преобразования выходного сигнала к 2-преобразованию входного сигнала и связана с импульсной характеристикой следующим образом:

Данная функция играет для цифрового фильтра ту же роль, что и передаточная функция для аналогового фильтра. Отметим, что задержка по времени входного сигнала на один отсчет приводит к умножению функции II (z) наг" ¹.