Расчет предварительно напряженного корпуса высокого давления

В качестве примера применения метода разделения переменных в осесимметричной задаче рассмотрим задачу определения напряженного состояния корпуса высокого давления (КВД). Подобные сооружения находят широкое применение в теплоэнергетическом строительстве, например в атомной энергетике. Конструкции таких корпусов достаточно слож;

ны, и комплексный анализ напряженного состояния в них может быть осуществлен либо численными, либо экспериментальными методами. Однако ряд принципиальных вопросов может быть решен на основании упрощенных моделей, в частности исследования влияния на напряженное состояние неоднородности, вызванной температурным полем.

Поскольку в КВД, которые, как правило, сооружаются из железобетона, иод действием эксплуатационных нагрузок (внутреннее давление и температура) возникают весьма значительные растягивающие напряжения, чтобы уменьшить или полностью устранить их, применяют предварительное обжатие в кольцевом и осевом направлениях. На рис. 5.10 представлена схема КВД, в котором обжатие в окружном направлении осуществляется путем равномерной навивки металлических тросов по внешней поверхности, что приводит к постоянному по высоте давлению. Другой способ предварительного обжатия заключается в приложении внешнего давления по поясам. Соответствующая схема показана на рис. 5.2.

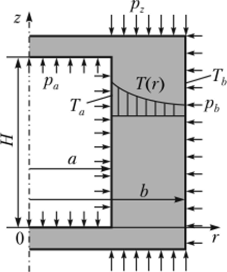
Рис. 5.10. Схема корпуса высокого давления.

Ниже приводятся результаты расчетов напряженного состояния КВД, подверженного действию постоянного по высоте температурного поля Г (г), внутреннего давления р_а, предварительного обжатия в осевом (р_г) и окружном (p_h) направлениях. При этом рассматриваются два способа приложения давления р_ь — равномерно по всей высоте КВД и, но поясам.

Будем считать приближенно, что изменение температуры вдоль радиуса соответствует решению уравнения теплопроводности для стационарного температурного поля в бесконечно длинном цилиндре:

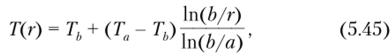
где Т_а и Т_ь — соответственно температуры на внутренней и внешней поверхностях корпуса. Зависимость модуля упругости бетона от температуры задается в соответствии с работой [30] и аппроксимируется полиномом четвертой степени. На рис. 5.11 показаны функции неоднородности Е{г) для нескольких значений Т_а при T_h = 20 °C. На основании анализа, проведенного в параграфе 3.4, при вычислении вынужденных (температурных) деформаций коэффициент линейного температурного расширения в рассматриваемом температурном диапазоне будем полагать постоянным (а_г= а_го).

Рис. 5.11. Изменение модуля упругости в стенке КВД.

Согласно выражениям (5.19) и (5.21) разложения в ряды Фурье внутреннего давления р_а и вынужденных деформаций е_в представляются лишь одним членом и соответствующие коэффициенты и функции имеют вид.

Здесь в силу осевой симметрии опущен индекс т. Коэффициенты разложения давления р_ь для случая, представленного на рис. 5.2, определялись, но формулам.

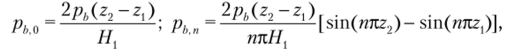
где //, — высота слоя, соответствующая периоду нагрузки. При равномерном внешнем боковом обжатии Я, может быть выбрана произвольно, например равной единице, а 2, = 0, h = H,

В результате расчета определялись перемещения и, w, напряжения ст_г, ст₀ и предварительные напряжения ст*°, к которым следует прибавить дополнительные напряжения а* (см. замечание 1 в подпараграфе 3.4.3), определяемые равенством.

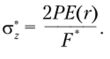
ь.

Здесь F' = 2к JE (f)rdr — приведенная площадь; Р — резуль;

я 2.

тирующая сила, равная Р = Р, — Р₂ — Р, где Р, = р_апа — сила, являющаяся результатом действия давления р_а на крышку корпуса; Р₂=р_гп (Ь² — а²) — и те тральное усилие от нредвари;

ь

тельного обжатия в осевом направлении; Р₃ = 2я|ст*°гс/г —.

а

равнодействующая напряжений ст*°, определяемых на предварительном этапе расчета.

Решение, полученное с учетом напряжений ст', не является точным во всей области. В частности, остаются неучтенными касательные напряжения, появляющиеся в зоне контакта стенки КВД с крышкой, а также нормальные напряжения, вызываемые неуравновешенными изгибающими моментами от напряжений а*⁰. Таким образом, согласно принципу Сен-Венана полученные результаты будут справедливы в средней части КВД.

Расчет КВД без учета температурной неоднородности На рис. 5.12 приведены эпюры напряжений, возникающих в стенке КВД от эксплуатационных нагрузок (р_а и Т), вычисленные при следующих исходных данных: а/b = 0,5; р_а = 5 МПа; Т_П = 100 °C; Т_ь = 20 °C; а_го = 0,12−10 ⁴ 1/°С;?₀ = = 3 • 10⁴ МПа; v = 0,2. Эпюры а. построены с учетом добавки а* без давления р_г. Напряжения ст, от давления р_а малы, так что суммарная эпюра а_г практически обусловлена лишь действием температурного ноля. Можно заметить, что в цилиндрической части КВД возникают весьма значительные напряжения ст₀ и а, от эксплуатационных нагрузок, которые необходимо компенсировать давлениями предварительного обжатия p_h и р_г При этом сначала необходимо выбрать давление p_h, поскольку оно приводит к изменению эпюры ст*⁰,.

после чего выбирается давление р_г, не влияющее на напряжения ст, и а₀.

Па рис. 5.13 приведены эпюры напряжений ст, на двух уровнях (z = 0 и z = 0,5Н) от эксплуатационных нагрузок (Ра⁼ 5 МПа; Т_а = 100 °C; Т_ь = 20°С) и для двух случаев бокового обжатия. При этом значение давления p_h выбиралось обратно пропорционально ширине пояса нагрузки:

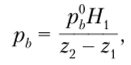
с тем чтобы интегральная величина бокового обжатия оставалась постоянной. Входящее в эту формулу давление p°_h соответствует равномерному обжатию по всей внешней поверхности.

Из приведенных на рис. 5.13 графиков можно заключить, что с уменьшением ширины пояса напряжения ст, от предварительного обжатия растут по абсолютной величине как в растянутой, так и в сжатой зонах. При этом если в сечении z = 0,5#, эти напряжения компенсируются напряжениями от эксплуатационных нагрузок, то в сечениях, близких.

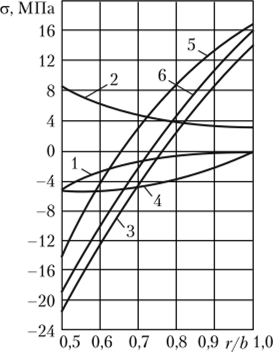
Рис. 5.12. Напряжения в стенке КВД:

Рис. 5.13. Напряжения ст, в стенке КВД:

• 1 — от эксплуатационных нагрузок; 2, 3 — от бокового обжатия:
• 2 — z, = 0,2#,; Z-, = 0,8#,;
• 3 — z, = 0,4#,; z₂ = 0,6#,

к торцу, эти напряжения суммируются, и для снятия растягивающих напряжений при более узком поясе нагрузки требуются большие сжимающие усилия в осевом направлении.

Расчет КВД с учетом температурной неоднородности Напряженное состояние КВД обусловлено суммарным действием внутреннего давления р_а, температурного поля и давлений предварительного обжатия р_ь и р,. Чтобы наглядно проследить влияние температурной неоднородности на напряженное состояние КВД, действие каждого из перечисленных факторов можно рассматривать отдельно.

В качестве примера на рис. 5.14 показаны эпюры ст₀ в стенке КВД от действия температурного поля с учетом и без учета зависимости Е (Т) при различных значениях температуры внутри корпуса (температура на внешней поверхности постоянна и равна T_h = 20 °C. Соответствующие графики Е (г) приведены на рис. 5.11.

В случае, когда Т_а = 50 °C, значения напряжений для однородного и неоднородного материалов практически совпадают. С ростом температуры происходит значительное падение модуля упругости, что ведет к уменьшению напряжений. Эти изменения более заметны в сжатой зоне, т. е. там, где температура выше. Аналогичный эффект наблюдается и при вычислении напряжений от внутреннего давления р_а.

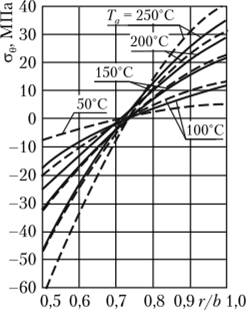
Рис. 5.14. Напряжения ст₀ в стенке КВД от действия температурного поля:

сплошная линия — неоднородный материал; пунктирная линия — однородный материал Заметное уменьшение напряжений от эксплуатационных нагрузок, полученное при учете температурной неоднородности бетона, позволяет снизить величину предварительного обжатия p_h, что в свою очередь ведет также к уменьшению осевого обжатия. Как показывают расчеты, при Т_а = 200 °C и при ширине пояса нагрузки z₂ — z, = 0,2Я, давление предварительного обжатия р_ь при учете неоднородности может быть уменьшено почти вдвое по сравнению с расчетом для однородного материала.