Методы регуляризации численных решений с большими градиентами

Кроме основных понятий теории разностных схем — аппроксимации, устойчивости, сходимости — на практике существенную роль играют дополнительные свойства разностных схем. Среди таких свойств упомянем монотонность. Не существует общепринятого определения монотонности разностной схемы. Пока, до рассмотрения разностных схем в пространстве неопределенных коэффициентов, где будут рассмотрены схемы с положительной аппроксимацией по Фридрихсу, воспользуемся определением, данным Дж. Борисом и Д. Буком^[1].

Под монотонными далее мы будем понимать такие разностные схемы, в которых не увеличивается число локальных экстремумов (минимумов и максимумов численного решения) по сравнению с числом локальных экстремумов в решении точной задачи. Кроме того, монотонные схемы не должны увеличивать по абсолютному значению уже имеющиеся экстремумы.

Свойство монотонности разностной схемы очень полезно при расчете разрывных решений. К сожалению, доказанная для линейного уравнения переноса теорема С. К. Годунова гласит, что среди линейных разностных схем (термин «линейный» мы уточним чуть ниже) не существует монотонных с порядком аппроксимации выше первого.

Зачастую в практических задачах схемы 1-го порядка аппроксимации не могут обеспечить требуемую точность численного решения.

При использовании немонотонных схем для получения численных решений с большими градиентами появляются осцилляции разностного происхождения. По этой причине в численных методах часто используется так называемая регуляризация численных решений. Рассмотрим наиболее распространенные методы регуляризации.

Сглаживание численного решения на верхнем слое (метод Л. А. Чудова). Вычисленное с помощью немонотонной разностной схемы значение функции в точке х_п корректируется следующим образом:

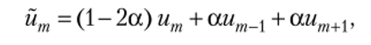
причем при, а = 0,5 значение й_т является средним арифметическим:

Чтобы понять действие сглаживающего оператора, представим явную схему для численного решения линейного одномерного уравнения теплопроводности.

Явная разностная схема имеет вид.

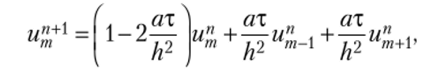
т.е. при а = ax/h² (это число — параболический аналог числа Куранта) сглаживание аппроксимирует диссипативный член, пропорциональный второй производной по пространственной координате. Понятно, что скорректированное решение будет устойчивым при, а < 0,5.

Для снятия последнего ограничения можно ввести алгоритм неявного сглаживания^[2]. Расчетная формула этого алгоритма имеет вид.

Аппроксимационная вязкость. Рассмотрим схему 1-го порядка аппроксимации для численного решения модельного однородного уравнения переноса (10.3):

Запишем для этой схемы ее первое дифференциальное приближение. Исследование этой схемы на аппроксимацию приводит к следующему выражению для главных членов ошибки аппроксимации (главных членов невязки):

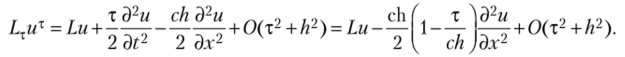
Таким образом, с точностью до членов 2-го порядка аппроксимируется уравнение.

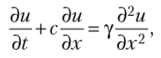
где у = 0,5с/г[1 — т/(с/г)] — так называемый коэффициент аппроксимационной вязкости, а член.

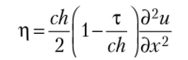
называется аппроксимационной вязкостью. Его действие — сглаживание численного решения. Действительно, вдоль характеристики последнее уравнение переходит в уравнение теплопроводности. Слагаемые в правой части уравнения переноса, пропорциональные второй производной, моделируют диссипативный эффект. Однако эта вязкость является свойством выбранной разностной схемы 1-го порядка аппроксимации. Здесь в уравнение не вводятся никакие дополнительные члены и не используются сглаживающие операторы. Рассматриваемое уравнение носит название первого дифференциального приближения разностной схемы (подробнее см. ниже). Все схемы 1-го порядка аппроксимации будут обладать схемной вязкостью.

Искусственная вязкость. Для регуляризации решения, полученного с помощью немонотонных разностных схем с порядком аппроксимации выше первого, можно вводить так называемую искусственную вязкость. Этот способ регуляризации решения был предложен К. Мортоном и Р. Рихтмайером^[3] для численного решения систем уравнений газовой динамики. В рамках данной главы мы ограничимся рассмотрением модельного линейного уравнения переноса.

Идею искусственной вязкости можно проиллюстрировать на примере, вообще говоря, неустойчивой схемы.

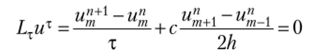
для решения линейного уравнения переноса (10.3).

Для того чтобы сделать эту схему устойчивой, введем в правую часть член порядка погрешности аппроксимации, моделирующий диссипативный эффект, так называемую искусственную вязкость. Мы получим задачу.

где 77(и",₊j — 2м" + м" _j) — искусственная вязкость, величина порядка «;

главного члена погрешности аппроксимации (невязки);? — коэффициент искусственной вязкости. Исследование этой схемы на устойчивость с помощью спектрального признака дает г < 0,5, а² < 2г, где г = ?, т/К¹, а = cx/h. При = 0,5 для рассматриваемого линейного уравнения получим схему Лакса — Вендроффа.

Методы коррекции потоков Бориса — Бука. Рассмотрим идею введения «антидиффузии», предложенную Дж. Борисом и Д. Буком¹. В дальнейшем разностные методы, аналогичные предложенным Борисом и Буком, получили название «методы коррекции потоков».

Пусть L_xu^x = 0 — схема 1-го порядка точности, аппроксимирующая линейное одномерное уравнение переноса (10.3) и обладающая аппроксимационной вязкостью. В качестве простейшего примера можно привести схему «явный левый уголок». Уменьшим влияние аппроксимационной вязкости на численное решение. Для этого введем потоки антидиффузии (терминология авторов метода):

где й_т — решение, полученное по схеме 1-го порядка с аппроксимационной вязкостью; Ф_т±½ — потоки. Отметим, что в современной литературе часто используются термины «числовой поток», «численный поток» или «функция числового потока».

Выражения для потоков имеют вид.

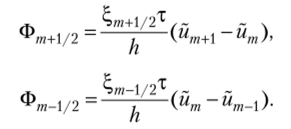
При постоянном значении ?, разностное уравнение имеет вид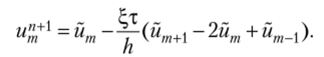

Основная идея метода коррекция потоков состоит во введении сглаживающего оператора определенного вида².^[4][5]

• [1] Борис Дж. П., БукД. Л. Решение уравнения непрерывности методом коррекции потоков // Вычислительные методы в физике. Управляемый термоядерный синтез. М.: Мир, 1980. С. 92−141.
• [2] Подробнее о сглаживании по Л. А. Чудову можно прочитать, например, в работе: Пасконов В. М., Полежаев В. И., Чудов Л. А. Численное моделирование процессов тепло-и массообмена. М.: Наука, 1984.
• [3] Рихтмайер Р., Мортон К. Разностные методы решения краевых задач. М.: Мир, 1972.
• [4] См. Борис Дж. П., Бук Д. Л. Указ. соч.
• [5] Метод коррекции потоков подробно описан в работе: Самарский А. А., Попов Ю. П. Указ. соч.